Skalárny súčin - LA2

Created by Jakub H

Môj pohľad na tému skalárny súčin.

#Lineárna Algebra, #Skalárny súčin, #dot product

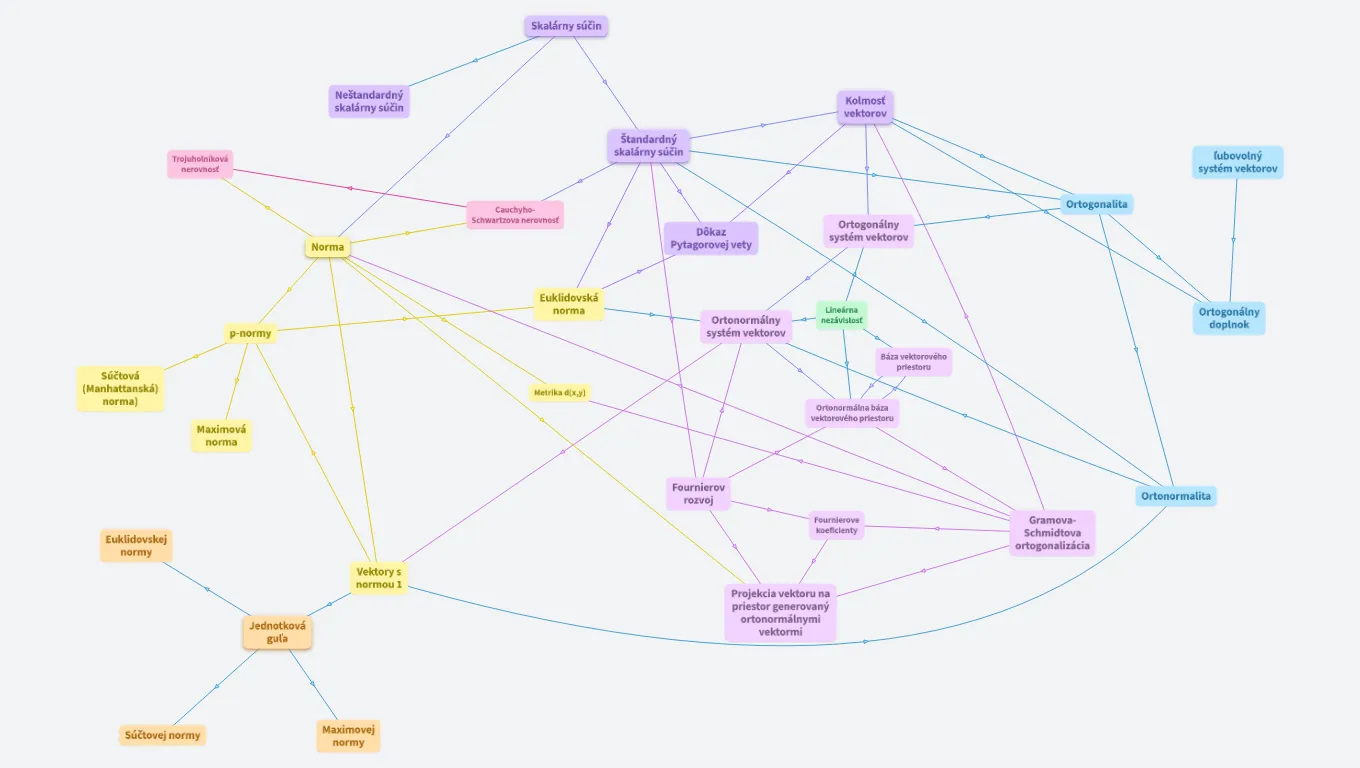
Skalárny súčin

Skalárny súčin: Zavedený axiomaticky

V je vektorový priestor nad R, potom skalárny súčin zavedieme ako zobrazenie V^2 --> R, a pre x,y,z IN V a b IN R platí.

1) <x,x> >= 0

2)<x+y,z> = <x,z> + <y,z> (linearita v prvej zlozke)

3)<bx,y> = b<x,y>

4)<x,y> = <y,x>

Neštandardný skalárny súčin

Kolmosť vektorov

Pre vyššiu ako 3 dimenziu už ťažko nahliadnuteľné. Preto kolmosť zavedieme ako:

x,y IN V sú kolmé keď <x,y> = 0

Trojuholníková nerovnosť

Štandardný skalárny súčin

Najbežnejši typ skalárneho S.

x,y IN R^n

<x,y> = SUM(i=1;i<=n;i++){ xi*yi}

ľubovolný systém vektorov

Cauchyho-Schwartzova nerovnosť

Ortogonalita

Norma

Zobrazenie V --> R , Určuje veľkosť vektoru. Norma je vždy nezáporná.

Dôkaz Pytagorovej vety

Ortogonálny systém vektorov

Euklidovská norma

p-normy

Ortonormálny systém vektorov

Lineárna nezávislosť

Ortogonálny doplnok

Báza vektorového priestoru

Súčtová (Manhattanská) norma)

Metrika d(x,y)

Maximová norma

Ortonormálna báza vektorového priestoru

Fournierov rozvoj

Ortonormalita

Euklidovskej normy

Fournierove koeficienty

Gramova-Schmidtova ortogonalizácia

Vektory s normou 1

Jednotková guľa

Je to množina vektorov, ktorých norma je <= 1. Pre každý typ normy vyzerá inak.

Projekcia vektoru na priestor generovaný ortonormálnymi vektormi