Číselné soustavy

Created by Pavel Honzík

JEDNIČKOVÁ (=UNÁRNÍ) SOUSTAVA

Nejjednodušší možná

DVOJKOVÁ (BINÁRNÍ) SOUSTAVA

Používá pouze dva znaky, a to 0 a 1

NEPOZIČNÍ ČÍSELNÉ SOUSTAVY

• jiná čísla, než základní jsou tvořena spojováním a opakováním čísel základních
• římské číslice
• zastaralé, moc se neužívají
• nevýhody: často neměly symboly pro záporná čísla  a nulu
• výhody: lehké sčítání a odečítaní

POZIČNÍ ČÍSELNÉ SOUSTAVY

Hodnota číslice je zde vyjádřena pozicí v určité řadě, která určuje  celkovou hodnotu čísla

-  vyjádření času

DESÍTKOVÁ (DEKADICKÁ) SOUSTAVA

• krátká soustava
  • Bilion znamená číslo 109 a další pojmenování následují vždy po tisícinásobku (trilion, kvadrilion)
  • USA, Velká Británie, Austrálie, Kanada 
• dlouhá soustava
  • 109 znamená termín miliarda, 1012  bilion, 1018 trilion, 1015 biliarda
  • kontinentální Evropa

Historie

PRAVĚK – znázornění podle nejdostupnějších prostředků – prsty, kamínky,…

- první obchodování, zavedení pětkové soustavy (V…5, X…10)

- speciální znaky pro čísla

- hieroglyfy nebo kombinace teček a vodorovných čárek

- pro astronomii a kalendářní výpočty používali speciální znaky pro čísla 0 – 19

- den má 24 h, hodina 60 min, minuta 60 sekund

-  nula je rovnocennou ostatním číslicím

- přispěli velkým dílem k vytvoření desítkové soustavy

→ Rozšíření do Arábie, Řecka, Itálie, a postupně po celém světe

DESÍTKOVÁ (DEKADICKÁ) SOUSTAVA

• Základem je číslo 10
• Používá symboly od 0 do 9
• Značení: 1623₁₀
• Odvozena od počtu prstů na rukou
• Nejrozšířenější
• Nejužívanější v běžném životě, vědě i technice

Číselné soustavy

Číselná soustava je způsob reprezentace čísel. Podle způsobu určení hodnoty čísla z dané reprezentace rozlišujeme dva hlavní druhy číselných soustav: poziční číselné soustavy a nepoziční číselné soustavy

V pozičních soustavách se hodnota čísla určuje na základě pozice jednotlivých číslic v zápisu. Nejznámější poziční soustavou je desítková soustava, kde se používají desetinné číslice od 0 do 9. Dalšími pozičními soustavami jsou např: binární (dvojková), oktální (osmičková), nebo hexadecimální (šestnáctková) .

Nepoziční soustavy jsou charakterizovány tím, že hodnota čísla se určuje na základě počtu jednotlivých symbolů v zápisu, nikoliv na základě jejich pozice. Příkladem nepoziční soustavy je např: římská soustava, kde se používají různé symboly pro různé hodnoty.

ŠESTNÁCTKOVÁ (HEXADECIMÁLNÍ) SOUSTAVA

16 znaků: číslice 0…9 a písmena   A…11, B…12, C…13, D…14, E…15, F…16

Kratší a přehlednější, než binární soustava

16=2⁴ → Jednoduchý převod mezi binární a šestnáctkovou soustavou

Značení: 657₁₆ , 657_H, nebo  657_HEX

• taktéž využití v IT technice
• programování webů 
• identifikace barev v PC
• zápis MAC adresy 

PŘEVODY

PŘEVOD MEZI BINÁRNÍ A DESÍTKOVOU

a) 20₁₀ "→" x₂

uČíslo stále dělíme dvěma a zbytek po dělení zapisujeme zprava jako výsledné číslo v binární soustavě

20  :  2  =  10  →  zb. 0

10  :  2  =  5  →  zb. 0

5  :  2  =  2  →  zb. 1

2  :  2  =  1  →  zb. 0

1  :  2  =  0  →  zb. 1

20₁₀ = 10100₂

PŘEVOD MEZI BINÁRNÍ A DESÍTKOVOU

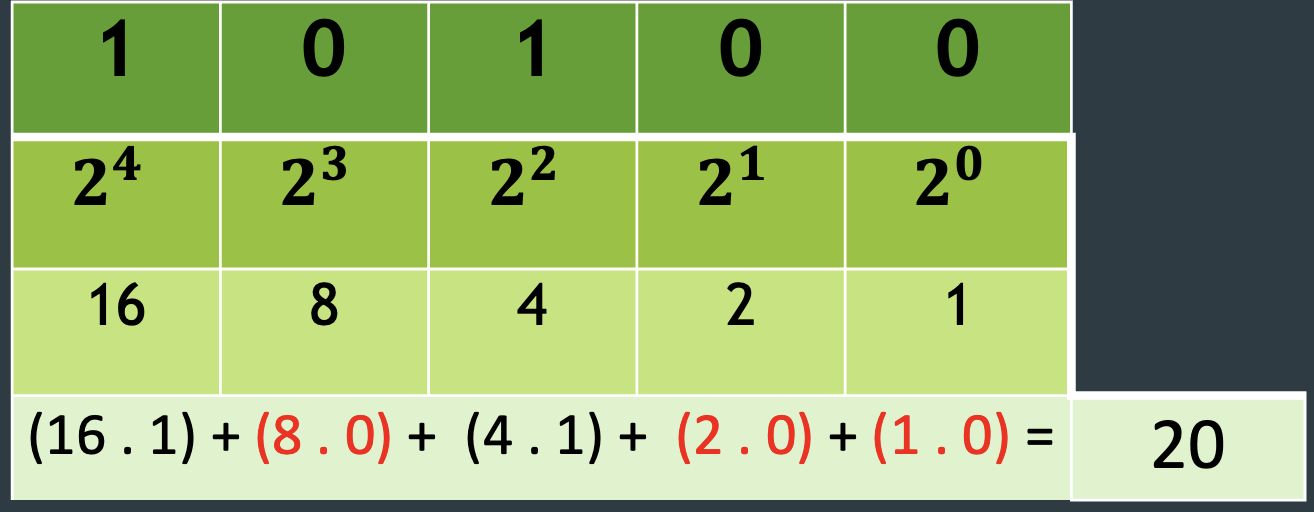
b)  10100₂ → x₁₀

Číslo vyjádříme pomocí mocnin čísla 2, které vynásobíme pozičními hodnotami, které nabývají hodnot 1 nebo 0

10100₂ → 20₁₀

PŘEVOD MEZI HEXADECIMÁLNÍ A DESÍTKOVOU

Př.: 185₁₀ = x₁₆

185  :  16  =  11  →  zb. 9

11  :  16  =  0  →  zb. 11

Číslo 185 by v 16 soustavě mělo tvar (11, 9)

místo „číslic“ nad 9 se používají písmena, takže 10 = A, 11 = B, 12 = C, …

→ 185₁₀ = B9₁₆

Naopak:

B9₁₆= x₁₀

B9₁₆= 11⋅16¹ + 9⋅16⁰ = 11⋅16 + 9 = 185₁₀

Řešení

PŘEVOD MEZI BINÁRNÍ A DESÍTKOVOU

a) 1623₁₀ → x₂

učíslo stále dělíme dvěma a zbytek po dělení zapisujeme zprava jako výsledné číslo v binární soustavě

1623  :  2  =  811  →  zb. 1

811  :  2  =  405  →  zb. 1

405  :  2  =  202  →  zb. 1

202  :  2  =  101  →  zb. 0

101  :  2  =  50       →  zb. 1

50  :  2  =  25     →  zb. 0

25  :  2  =  12    →  zb. 1

12  :  2  =  6       →  zb. 0

6  :  2  =  3      →  zb. 0

3  :  2  =  1       →  zb. 1

1  :  2  =  0       →  zb. 1

1623₁₀ → x₂ = 11001010111₂

PŘEVOD MEZI BINÁRNÍ A DESÍTKOVOU

b) 11001010111₂ → x₁₀

Číslo vyjádříme pomocí mocnin čísla 2, které vynásobíme pozičními hodnotami, které nabývají hodnot 1 nebo 0

 11001010111₂ = 1623₁₀

PŘEVOD MEZI HEXADECIMÁLNÍ A DESÍTKOVOU

1623₁₀ → x_HEX

učíslo stále dělíme šestnácti a zbytek po dělení zapisujeme zprava jako výsledné číslo v hexadecimální soustavě

1623    :     16  =  101    →  zb. 7

101   :    16  =  6      →  zb. 5

6    :    16  =  0     →  zb. 6

1623₁₀ = 657_HEX

PŘEVOD MEZI HEXADECIMÁLNÍ A DESÍTKOVOU

b) 657_HEX →x₁₀

Číslo vyjádříme pomocí mocnin čísla 16, které vynásobíme pozičními hodnotami

657_HEX →1623₁₀

Videa

Řešení

Řešení