Functional Analysis

Created by Lukas Juhrich

Pairing σ(X, X')

Weak top on X

Weak* top on X'

Arzela Ascoli

Sufficient for compness of M sub C(K):

M bounded, closed, and equicontinuous

M bounded iff weakly bounded

Banach-Alaoglu: B1 weak*-compact

Equicontinuity

For aa set of f: S→ℝ, we have:

1. ∀ε ∀f ∃δ. […] (every f continuous)
2. ∀ε ∃δ ∀f. […] (equicontinuity)

(xᵢ)ᵢ σ-conv ⇒ bounded

(Tᵢ) conv pointwise ⇒ conv

Compact operators

• meagre: ctbl. union of nowhere dense
• nowhere dense: int cl = ø

Compness in Lᵖ(ℝ)

Sufficient: M bounded, closed, and

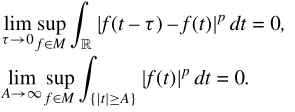
contrapositive: Pigeonhole for ctbl decomposition of set with nonempty interior!

Baire CT

in a complete metric space,

1. \cap_ℕ open dense = dense
2. \cup nowhere dense = nowhere dense
3. co-meagre ⇒ dense.

examples

Yes:

• 𝓁ᵖ, Lᵖ, 𝕂ⁿ

No:

• C(K):
• L∞: 
• Hence L¹ also not

Y Ban: K(X,Y)≤L(X,Y) closed

Banach-Steinhaus

Ctx: L(Ban, Norm)

{‖Tᵢx‖}ᵢ bounded ∀x ⇒{‖Tᵢ‖}ᵢ bounded

lim Kₙ remains compact

T: X→Y closed: lim (xᵢ, Txᵢ) in Gr T (if exists)

cl ≤ refl is refl

X refl iff X' refl

T closed surj ⇒ open; +inj ⇒ T⁻¹ cont

Open mapping: Surj between Banach spaces are open

T linear closed ⇒ cont

X refl ⇒ weakly seq. compact

every bounded seq xᵢ has a weakly convergent subseq

Weak conv / Refl

Banach norm dominates other ⇒ equivalent

Inj is embedding iff im closed

Closed image thm

Tfae:

1. ran T closed
2. ran T = (ker T')\perp
3. ran T' closed
4. ran T' = (ker T)\perp

Graph norm ‖x‖+‖Tx‖ ≥ ‖x‖

to prove X irreflexive: find bounded seq withhout weakly convergent subseq.

closed conv ⇒ weakly closed

Ban ≤ Nor reflective

X comp ⇒ U≤X comp iff cl

ι:X→X'' is a nat. isometry into a BanSp

c₀≤𝓁^∞ not complemented

C conv in H. F: C→C nonexpansive has a FP.

(X/U)' ≅ U^⟂
U' ≅ X'/U^⟂

Y comp ⇒L(X,Y) comp

X' is pretty inhabited!

Motto: X' is pretty inhabited! ∃x'…

• mapping x ↦ 1
• mapping U↦0, but x↦≠0
• separating x≠y

Also, ‖x'‖=1 are enough to reconstruct ‖x‖.

‖x‖ = ‖_(x)‖

X' comp

ConvSep I: V₁ vs V₂

V₁, V₂ convex, V₁ open.

∃x': Re x'(V₁)<x'(V₂).

Hahn-Banach (Nor)

ConvSep II: V vs. x

V closed convex, x not in V.

∃x': Re x'(x) < inf Re x'(V)

→ℂ extends w/ same norm

We have

Re(u'(x)) = |u'(x)| ≤ ‖u'‖‖x‖ =: p(x)

Thus extension satisfies

Re(x'(x)) ≤ ‖u'‖‖x‖

Now rotate to optimize the LHS to |x'(x)|.

→ℝ extends w/ same norm

We have |u'(x)| ≤  ‖u'‖‖x‖ =: p(x)

→ℝ extends ≤p

• l: U→ℝ
• p: V→ℝ sublin
• l ≤ p

Then l extendable to L.

→ℂ extends Re≤p

• l: U→ℂ in ℂ-Vec
• p: V→ℝ sublin
• Re l ≤ p

Then l extendable to L.

sublinear → ℝ

n.n. >0!

• Subadditive: q(x+y)≤q(x)+q(y)
• Homog. for λ>0

Homℝ(V→ℝ) factors as Re of Homℂ(V→ℂ)

Set x↦L(x)-iL(ix)

U+xℝ step

Have: L(u) ≤ p(u)
Want:

L(u±λx) ≤ p(u±λx) ∀λ>0,u in U
… ⇔  L(u±x) ≤ p(u±x) ∀u in U
… ⇔ ± Lx≤ p(u±x)-Lu ∀u in U
… ⇔ Lu-p(u-x) ≤ Lx ≤ p(u+x)-Lu ∀u in U

But this works, because

Lu+Lv≤ p(u+v)≤ p(u+x)+p(v-x)