Constraint satisfaction and optimization (backup #12)
Created by Martin Dvořák
#computer science

Succeed first
Fail first
Integer factorization
Given an integer N and an integer M with 1 < M < N, does N have a factor d with 1 < d ≤ M ?
Graph isomorphism problem
Both graphs are written on the input.
Existing CSP libraries
Planning
Value ordering
Variable ordering
Algorithms
Scheduling
SAT
AI for games
Graph coloring
General ordering
to apply both together during the search is the best thing to do in general
Domain-specific heuristics
A*
Iterative-broadening search
Horn-SAT
Applications
NAE-SAT
Types
Usage
Breadth-first search
Queue (FIFO)
3-SAT
Heuristics
Simplex method
2-SAT
1in3-SAT
Graph homomorphism problem
Target graph is fixed.
Graph choosability
Depth-first search
Stack (LIFO)
Linear data structures
Abstract data structure
Ellipsoid method
Ladner (1975)
Ladner's theorem:
P = NP holds IFF the class NP-intermediate is empty
https://dl.acm.org/doi/10.1145/321864.321877
3,3-SAT
Boolean CSPs
Both the domain and the codomain are {true, false}.
Promise CSPs
Solving algorithms
State-space search
Use
Backtrack-free search
Iterative-deepening search
Existing LP libraries
NP-intermediate
Schaefer (1978)
Original formulation:
A finite set of relations S over the Boolean domain defines a polynomial time computable satisfiability problem if any one of the following conditions holds:
- all relations which are not constantly false are true when all its arguments are true;
- all relations which are not constantly false are true when all its arguments are false;
- all relations are equivalent to a conjunction of binary clauses;
- all relations are equivalent to a conjunction of Horn clauses;
- all relations are equivalent to a conjunction of dual-Horn clauses;
- all relations are equivalent to a conjunction of affine formulae. [2]
Otherwise, the problem SAT(S) is NP-complete.
https://dl.acm.org/doi/10.1145/800133.804350
Modern formulation:
Let Γ be a finite constraint language over the Boolean domain. The problem CSP(Γ) is decidable in polynomial-time if Γ has one of the following six operations as a polymorphism:
- the constant unary operation 0;
- the constant unary operation 1;
- the binary AND operation ∧;
- the binary OR operation ∨;
- the ternary majority operation {\displaystyle \operatorname {Majority} (x,y,z)=(x\wedge y)\vee (x\wedge z)\vee (y\wedge z);}

- the ternary minority operation {\displaystyle \operatorname {Minority} (x,y,z)=x\oplus y\oplus z.}

Otherwise, the problem CSP(Γ) is NP-complete.
CSP in AI

P != NP
assumption
Hell, Nešetřil (1990)
Let H be a simple graph. H-coloring is polynomial-time solvable IFF the graph H is bipartite.
https://doi.org/10.1145%2F800133.804353
Linear programming
Zhuk (2017)
tractable IFF has a weak near unanimity polymorphism
https://arxiv.org/abs/1704.01914
Random walk
Local search
Consistency techniques
Thapper, Živný (2015)
https://doi.org/10.1007/978-3-662-47672-7_86
Dichotomy theorems
Enforcing algorithms
AC-3
Sherali, Adams (1988)
https://doi.org/10.1137/0403036
P

NP-complete

Siggers polymorphism
AC-4
Genetic algorithms
Evolutionary algorithms
Simmulated annealing
Money money money
Basic LP relaxation
Sherali-Adams hierarchy
CSPs
a.k.a. crisp languages
All cost functions are restricted to values zero and infinity.
(Fixed-language) CSPs can also be equivalently expressed as a search for a homomorphism from an input structure A to a fixed structure B.
NP

Weak near-unanimity polymorphism
Cyclic polymorphism
Evolutionary programming
Genetic programming
Types of consistency
Kolmogorov, Thapper, Živný (2012)
https://arxiv.org/abs/1311.4219
0-Extensions of graph metrics
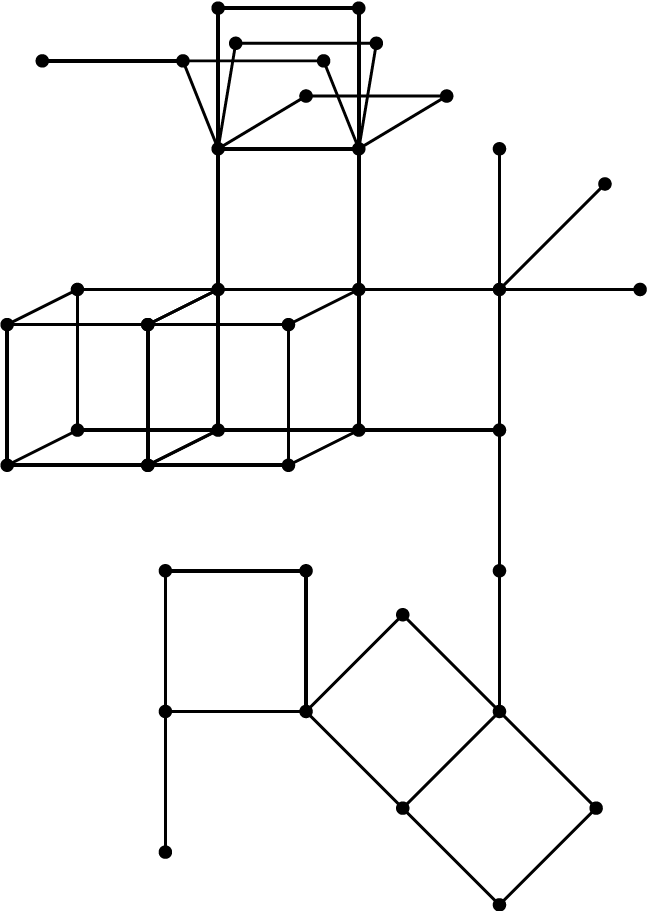
Another case of "easy"
Thapper, Živný (2012)
tractable IFF admits a binary symmetric fractional polymorphism
https://arxiv.org/abs/1210.2987
Kolmogorov, Rolínek, Krokhin (2017)
conjunction of the previous two results is both necessary and sufficient for tractability in the general case
https://arxiv.org/abs/1502.07327v5
"Easy"
Complexity classes
Polymorphism for a language
Directed-arc consistency
Path consistency
Taylor operation
Economy
Expansion Lemma
CSP in general

Multifacility location problem
Relation width

 Beware of missing \dots in the description (8)
Beware of missing \dots in the description (8)
Tractability properties (AND)
NP-hard

Symmetric fractional polymorphism
All permutations of arguments must yield to the same output.
Clone
a set of functions that
(1) contains all projections
(2) closed under superpositions
Identities
a.k.a. functional equations
General k-consistency
Arc consistency
Fractional polymorphism

Resource-production optimization
Hereditary modularity
Max-Cut problem
Submodular function
Associative operation
Karzanov (2004)
tractable IFF weighted-modular and 4-orientable
https://doi.org/10.1016/j.dam.2003.05.005
Reduction
Strong k-consistency
General-valued
Cost functions have any rational* values (integer fractions or infinity).
Generalized fractional polymorphism
Operations are grouped into sets with equal weights among each set.
Weighted polymorphism
Neightbourhood inverse consitency
Karzanov (1998)
tractable IF hereditary modular and 4-orientable
intractable IF non-modular
intractable IF not 4-orientable
https://doi.org/10.1006/eujc.1997.0154
Karzanov E-consistent polymorphism
Commutative operation
Min-Cost-Hom
Cost functions or arity > 1 are restricted to values zero and infinity.
Modularity
(MC) condition
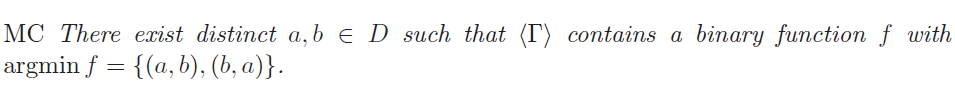
(MC') condition
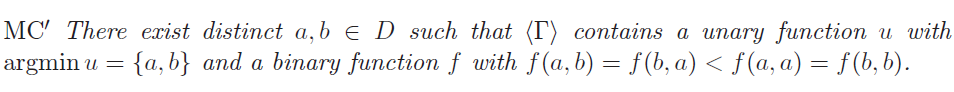
"Hard"
Finite-valued
All cost functions are restricted to finite values.
Symmetric generalized fractional polymorphism
Galois correspondence
Core
for each label exists a unary function with a strict minimum there
Fixed-template
Our interest: What are the classes of discrete functions that admit an efficient minimisation algorithm?
General Min-Sum problem
Conservative language
can express all unary functions
Karzanov's orientability
Any tracktable finite-valued language
Computational complexity
Max CSPs
All cost functions are restricted to values zero and one.
Arity
unary VCSPs are always trivial
binary VCSPs already have the majority of complications that are present in general-arity VCSPs
Acyclic E-consistent polymorphism
E-consistent polymorphism
E-antipodal polymorphism
symmetric generalized fractional polymorphism of arity 2 -> 2 such that all pairs are antipodal with respect to the graph of cost functions with |argmin(f)| = 2
Gamma_c

Structural restrictions
Hypergraph formed by sets of variables appearing in individual constraints is restricted.
S-parallel operations
<Gamma>

Graph for unary functions with |argmin| = 2
VCSP
Valued Constraint Satisfaction Problem
Generalization of CSP
Subfield of Mathematical optimization
The domain can by anything, but we will focus on finite sets.
The codomain can be any ordered monoid, but we will focus on (non-negative) rational (real) numbers with positive infinity.
S-antipodal operations
Optimization problems
Decision problems
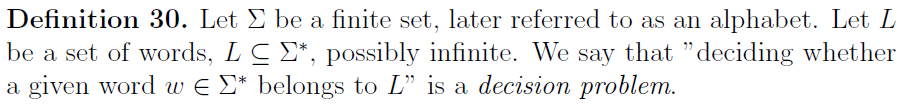
Threshold-decision version
Regex
Automata
Finite automata
Regular languages
Stack machines
Grammars
Non-deterministic stack machines
Context-free languages
Linearly-bounded machines
Context-sensitive languages
Turing machines

Always halts?
Recursive languages
Recursively-enumerable languages
