Complex numbers are NOT numbers
Created by Pavel Klavík
Gauss deciphered complex numbers over 200 years ago, yet they still remain mysterious for most. Two geometric meanings are explained: points of the plane and transformations of the plane.
#Gauss, #complex numbers, #history, #linear algebra, #math, #mathematics, #matrices, #numbers
Complex numbers are NOT numbers
| Pavel Klavík, PhDfounder and CTO
of OrgPad |
Surrounded by clouds of mystique
“Only by abandoning math's connection to reality could we discover the reality's true nature.”
Great history overview
Let's demystify complex numbers
Geometric meaning of complex numbers
What are roots of negative numbers
Short history of complex numbers
Not needed for quadratic polynomials
Cardano 1545
“as subtle as it is useless”
Bombelli 1572 and 1579
This presentation
Descartes 1637
Coined the term “imaginary”:
“For any equation one can imagine as many roots [as its degree would suggest], but in many cases no quantity exists which corresponds to what one imagines.”
Euler 1777
Introduced the notation 𝑖 and called it impossible.
Wessel 1797
Argand 1806
Gauss 1831
|
“If this subject has hitherto been considered from the wrong viewpoint and thus enveloped in mystery and surrounded by darkness, it is largely an unsuitable terminology which should be blamed. Had +1, -1 and √ −1, instead of being called positive, negative and imaginary (or worse still, impossible) unity, been given the names say, of direct, inverse and lateral unity, there would hardly have been any scope for such obscurity.” |
Let's fix this!
And you can help!
Geometry of the plane
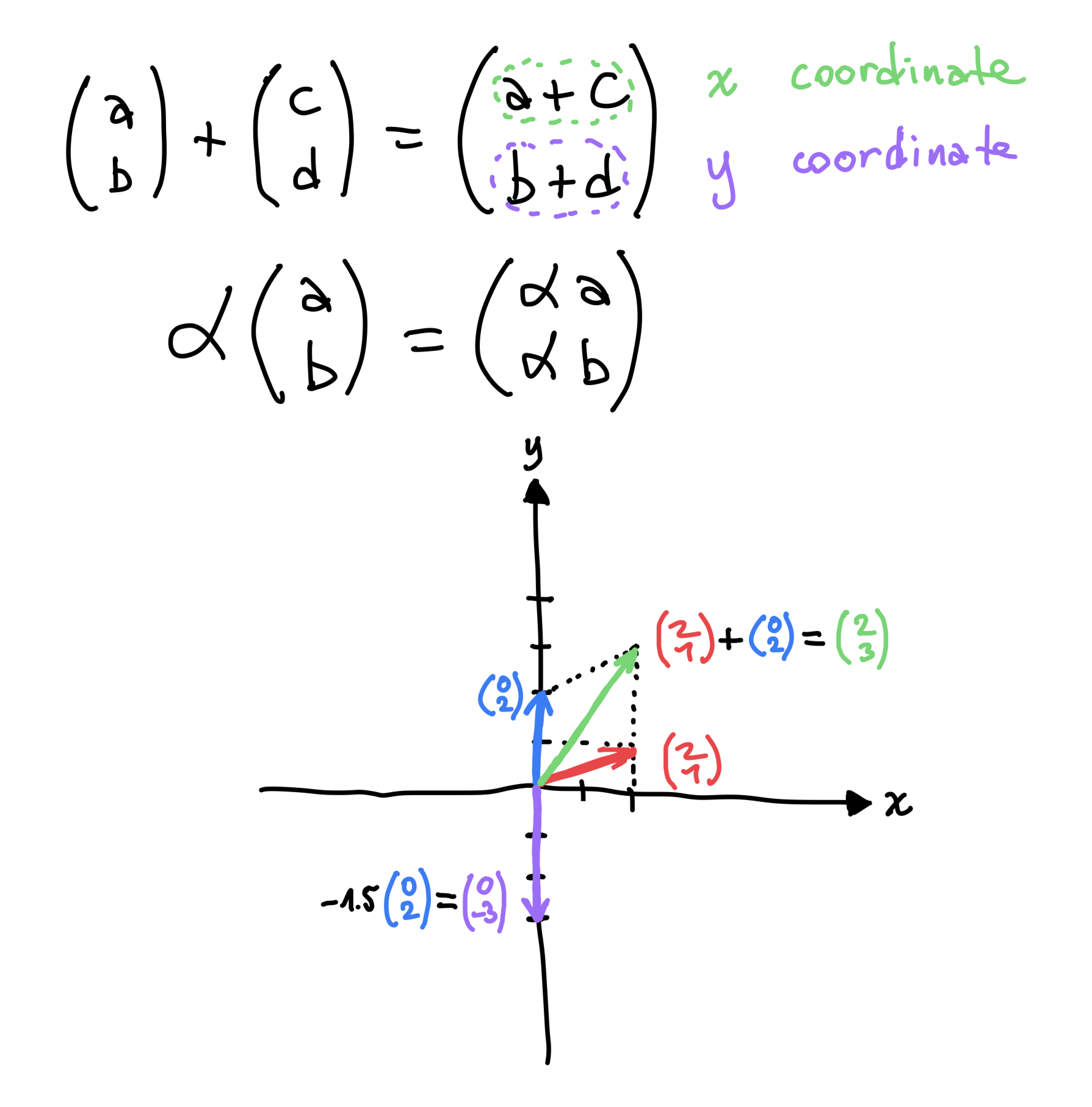
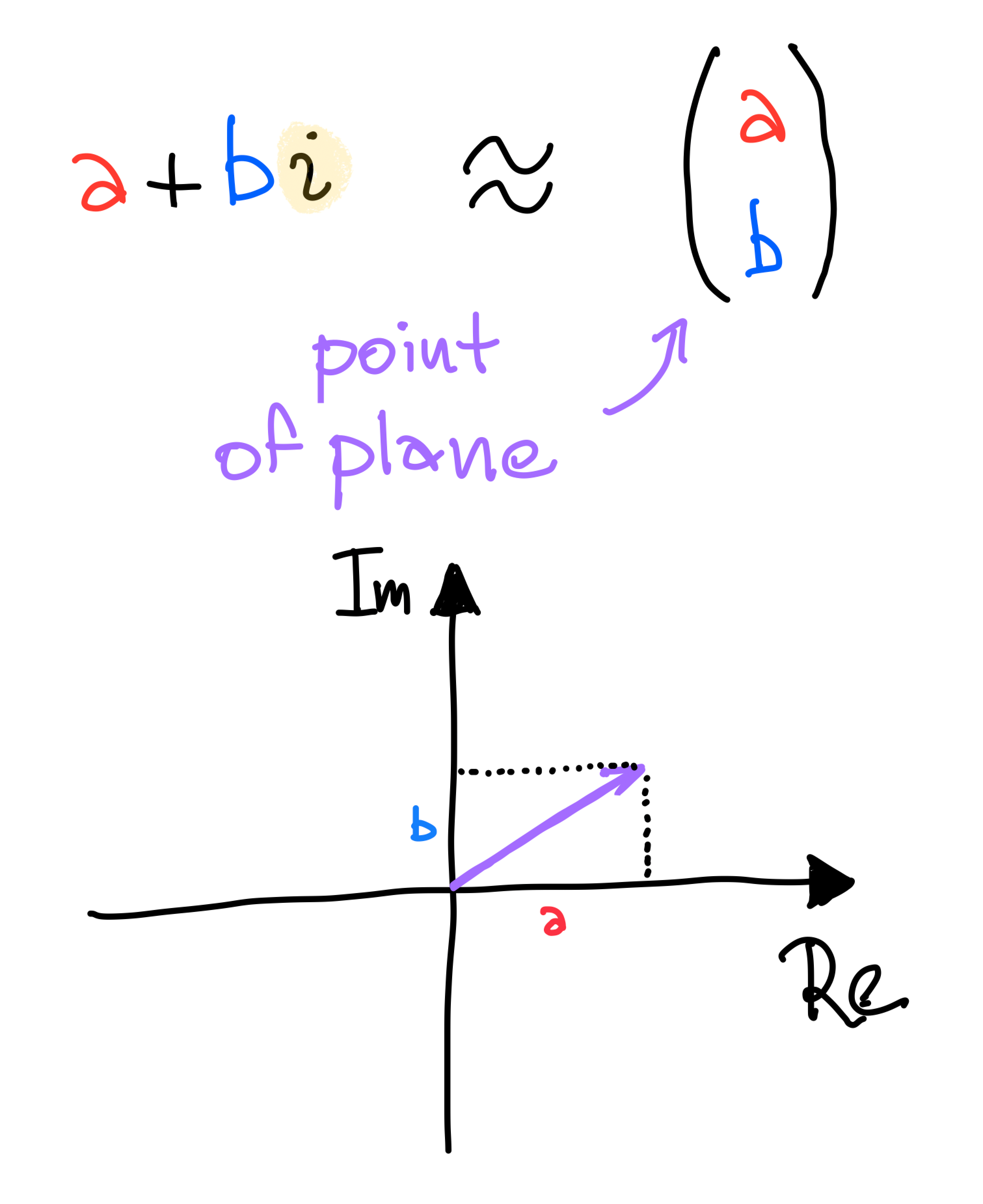
Points of the plane
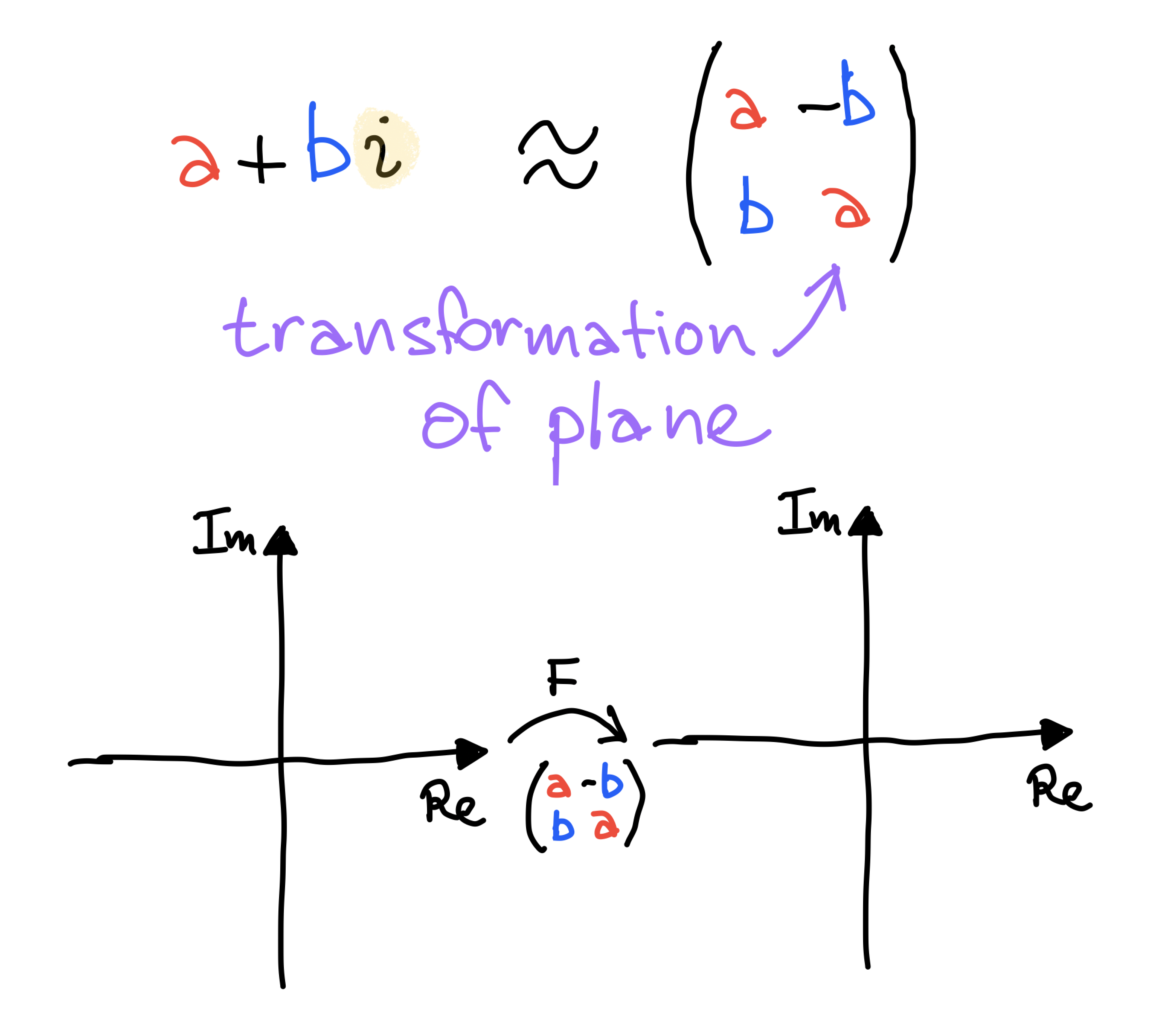
Transformations of the plane
Scaling
Rotation
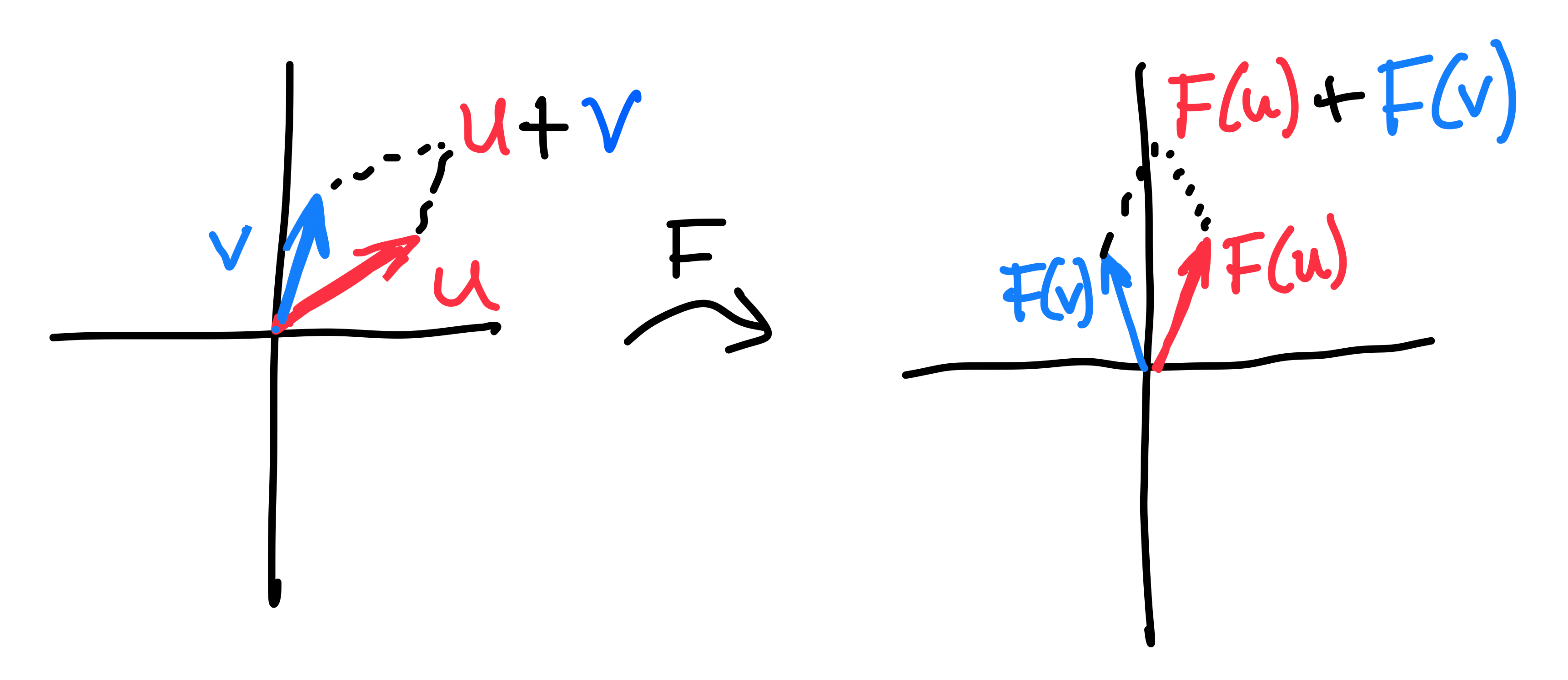
Reflection
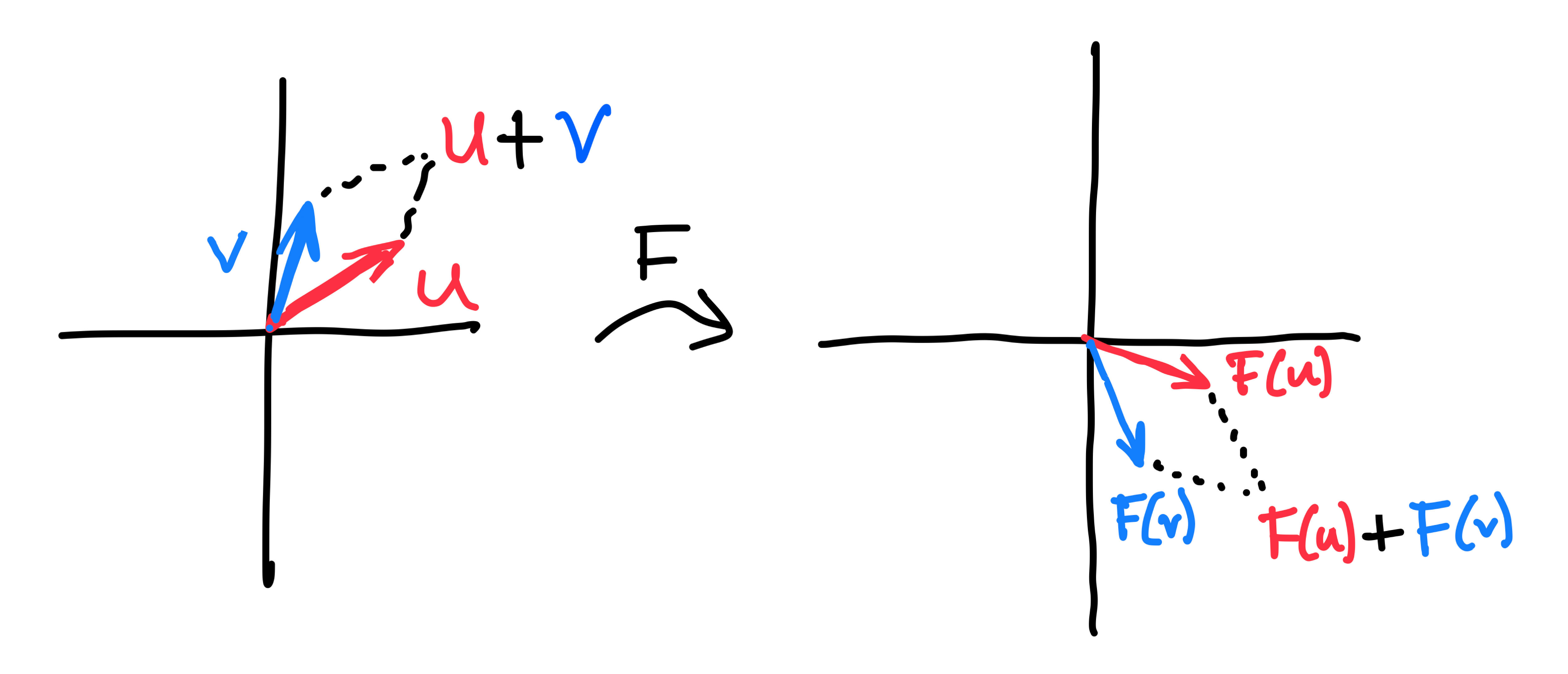
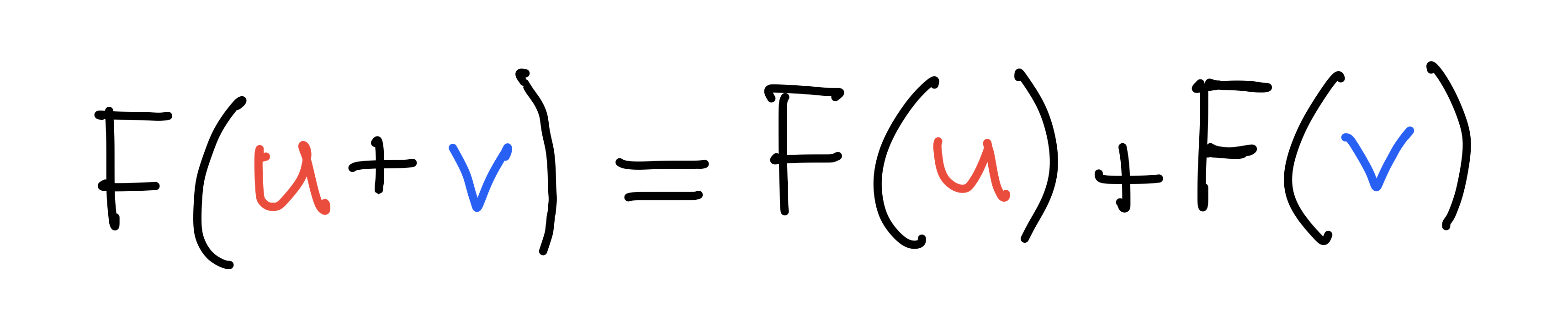
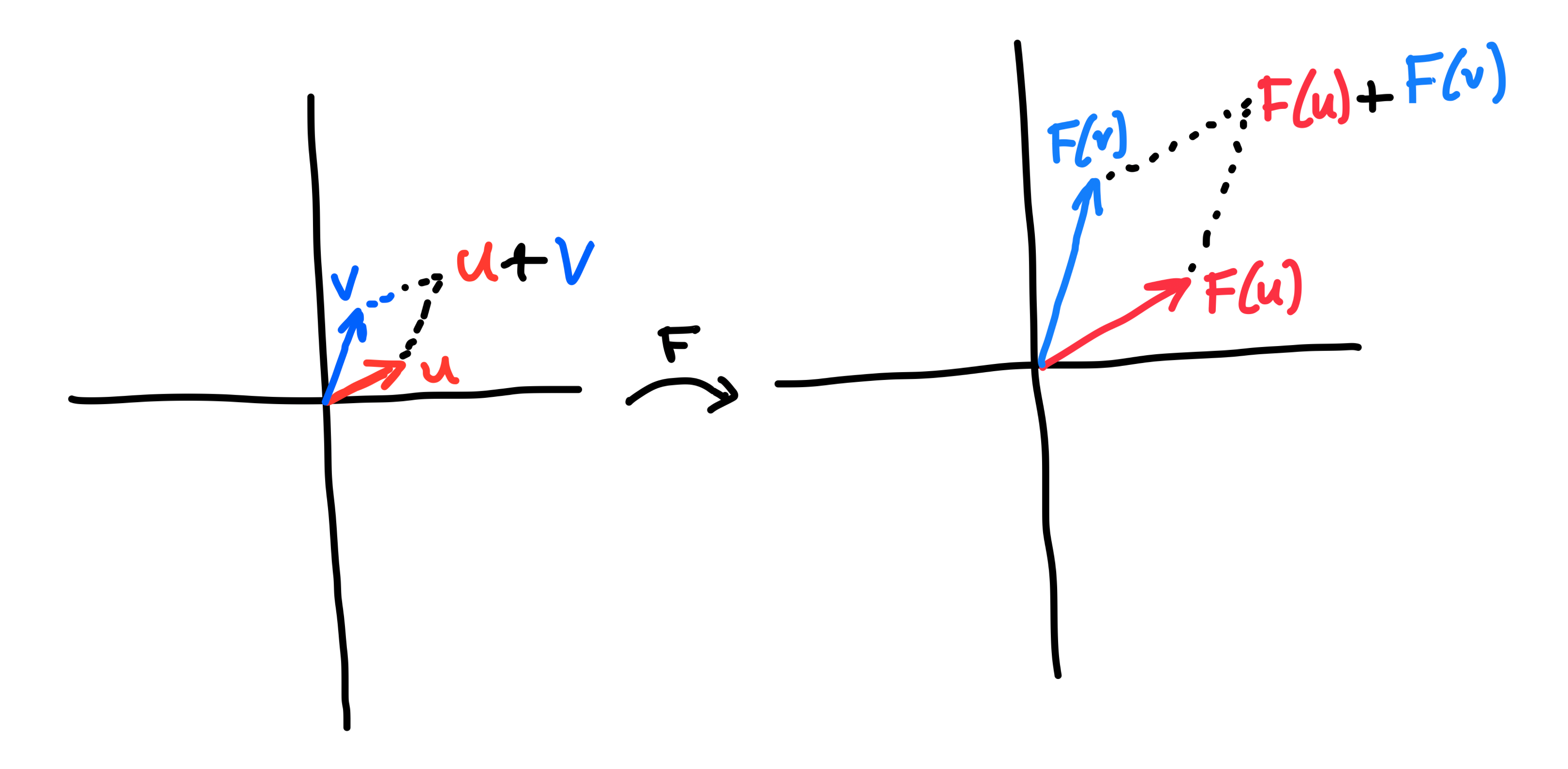
Linear transformations
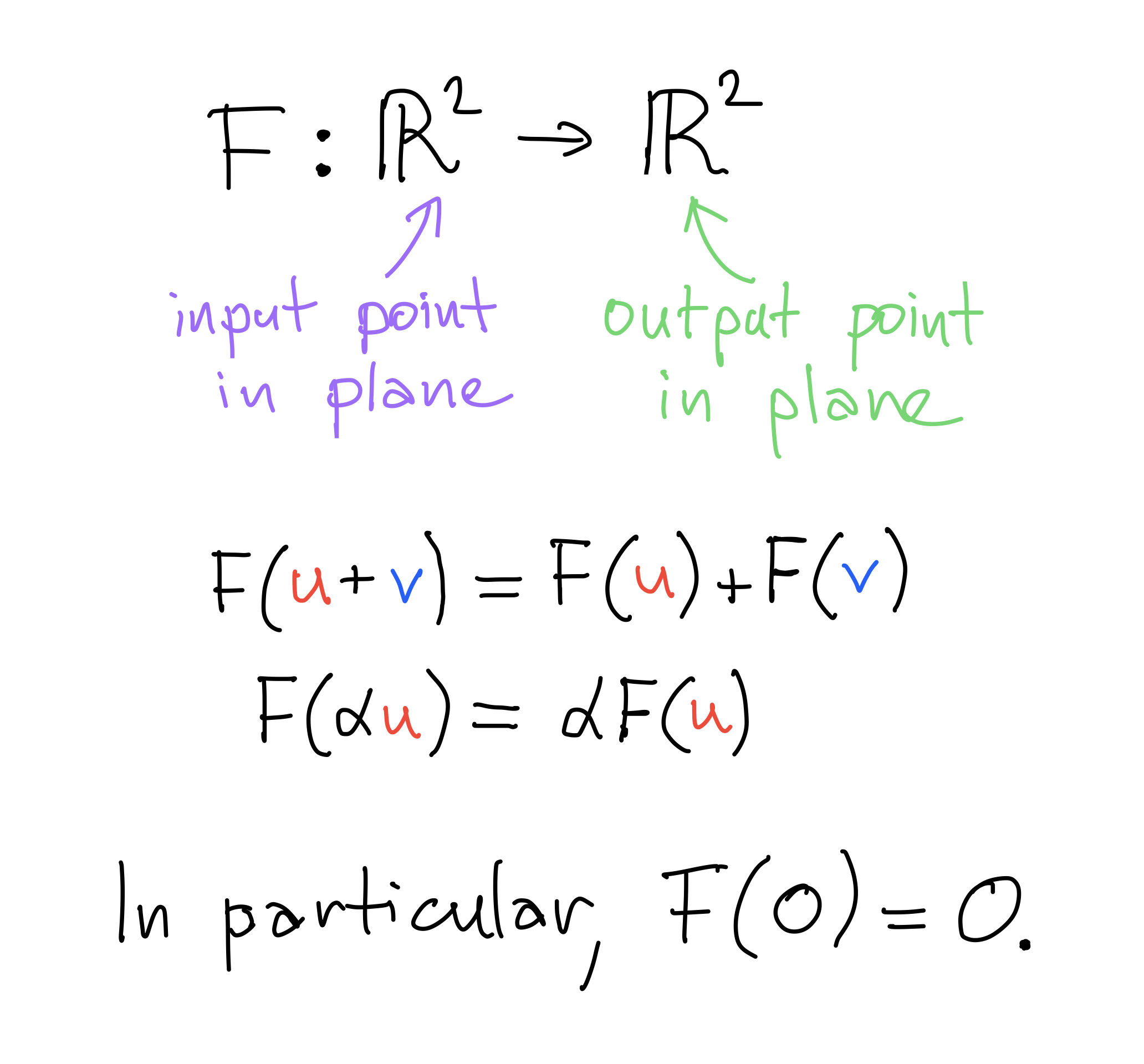
Translation is not a linear transformation
How to describe a linear transformation?
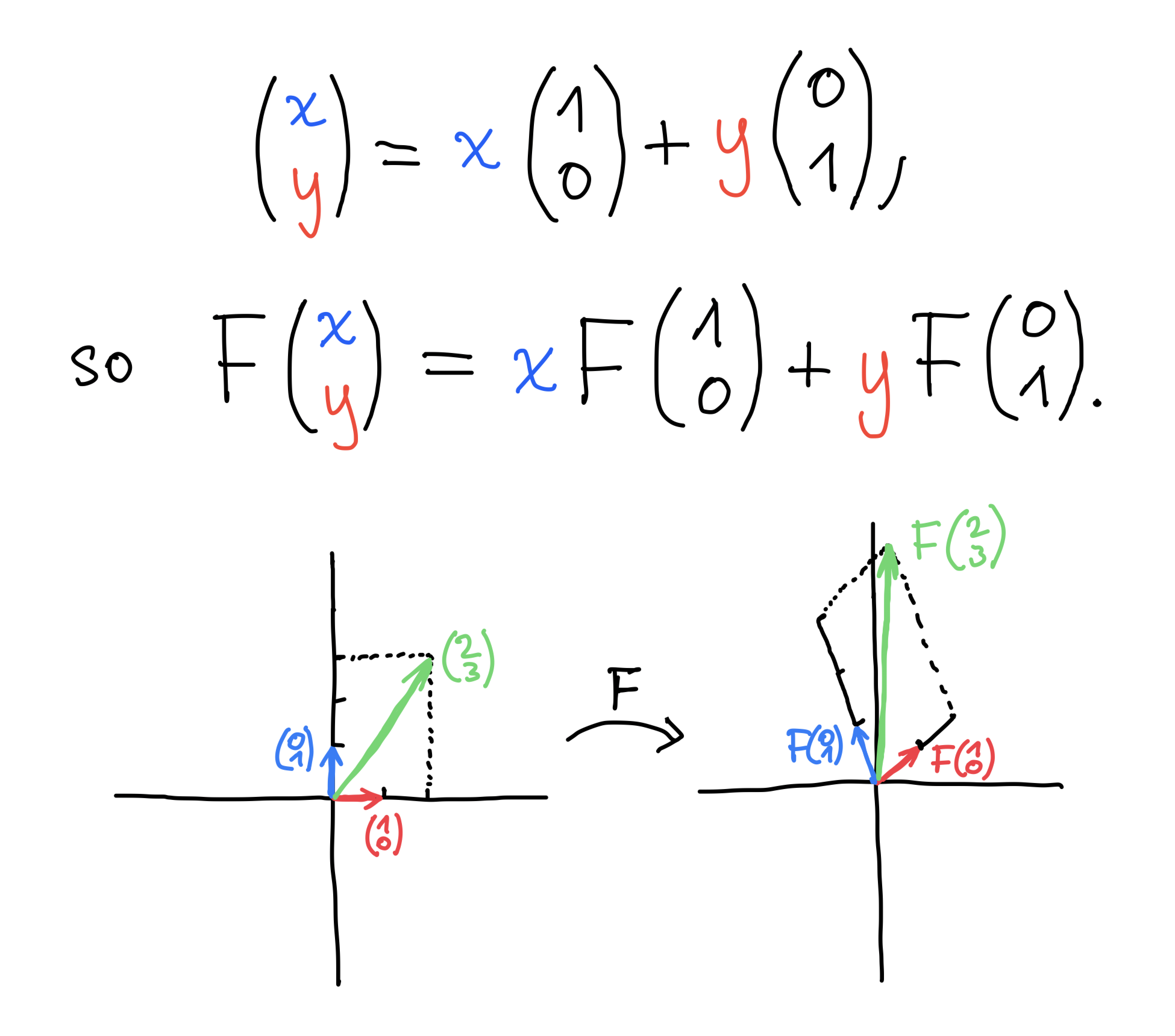
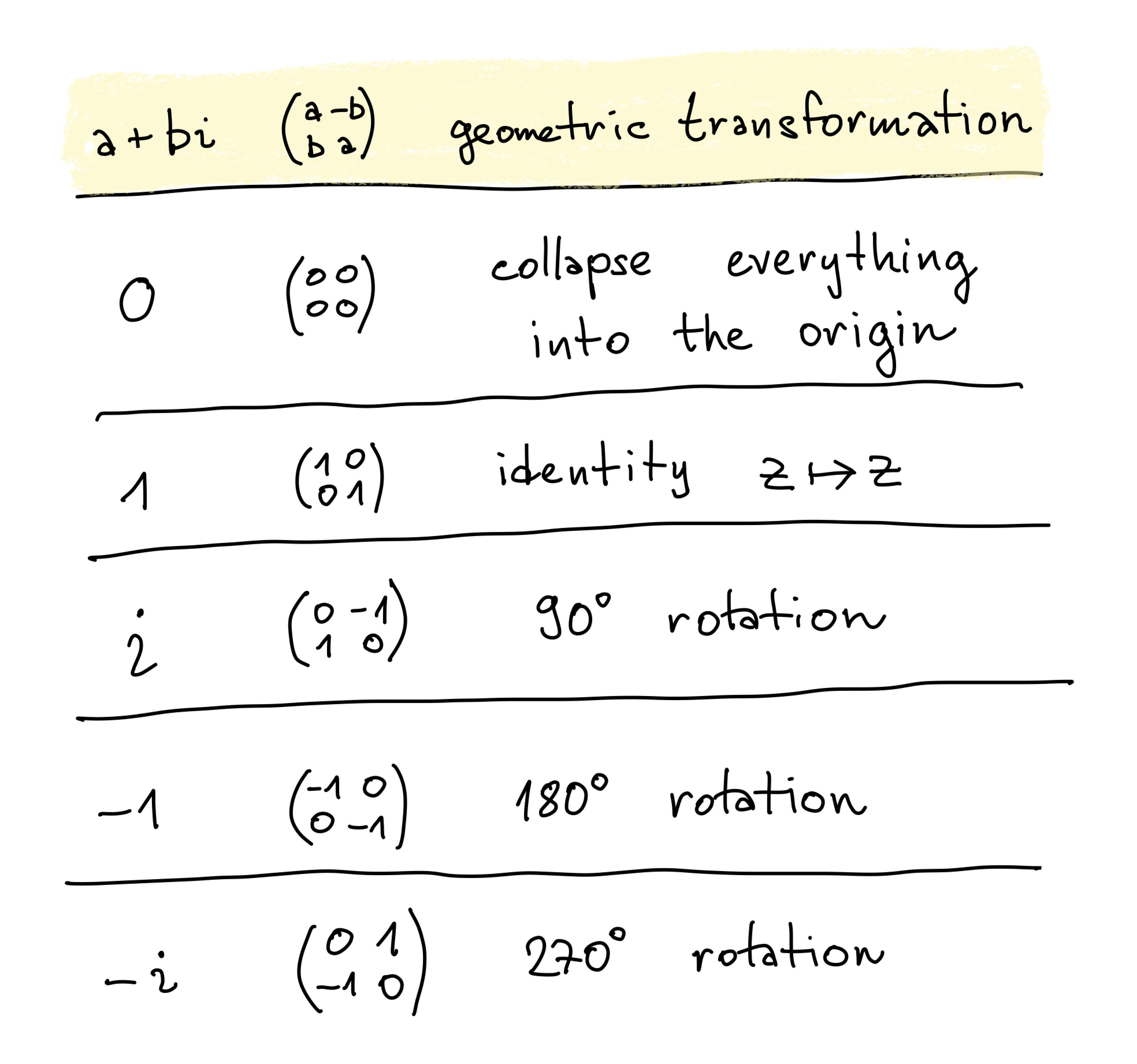
Matrix representation
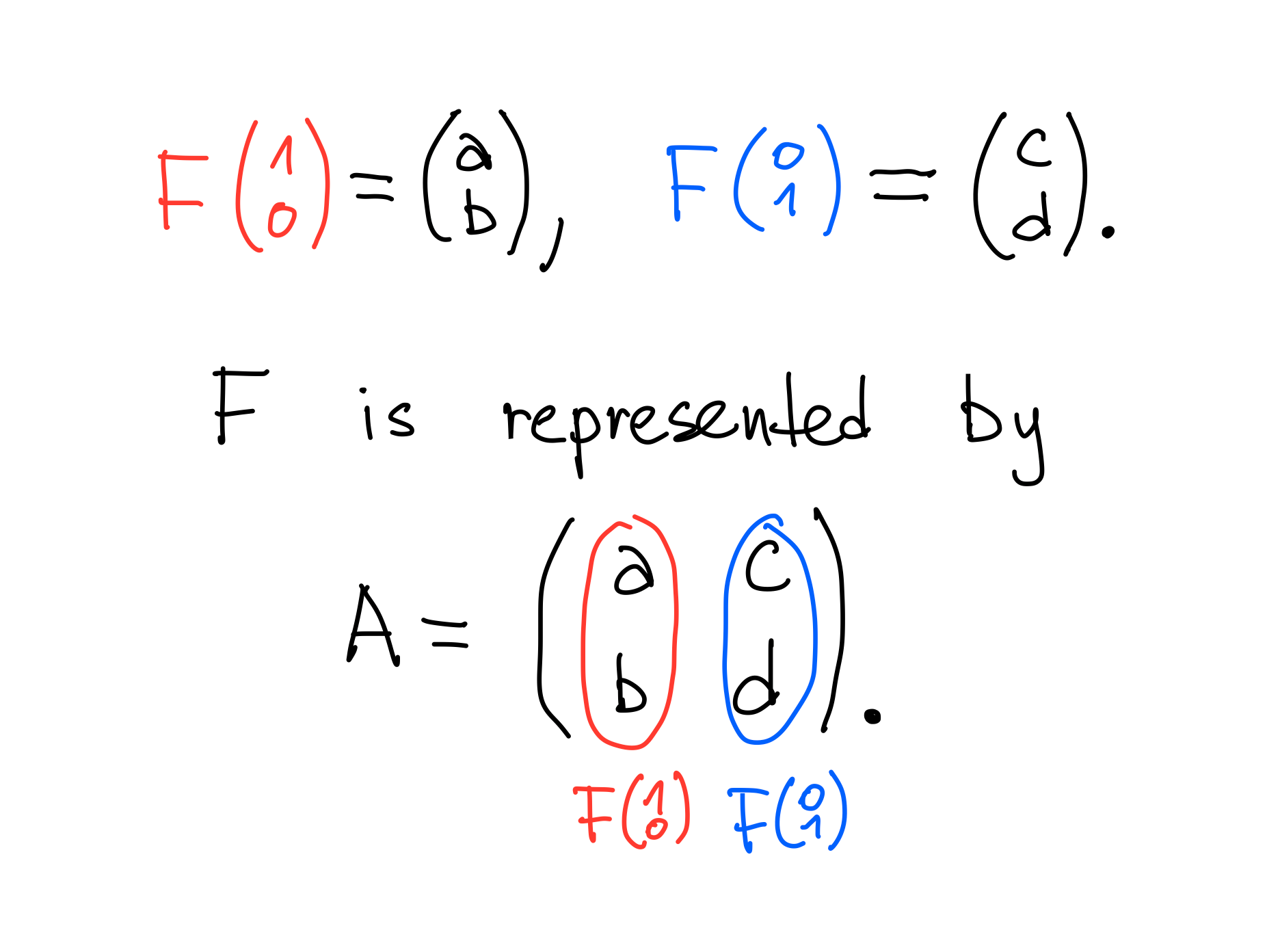
Examples
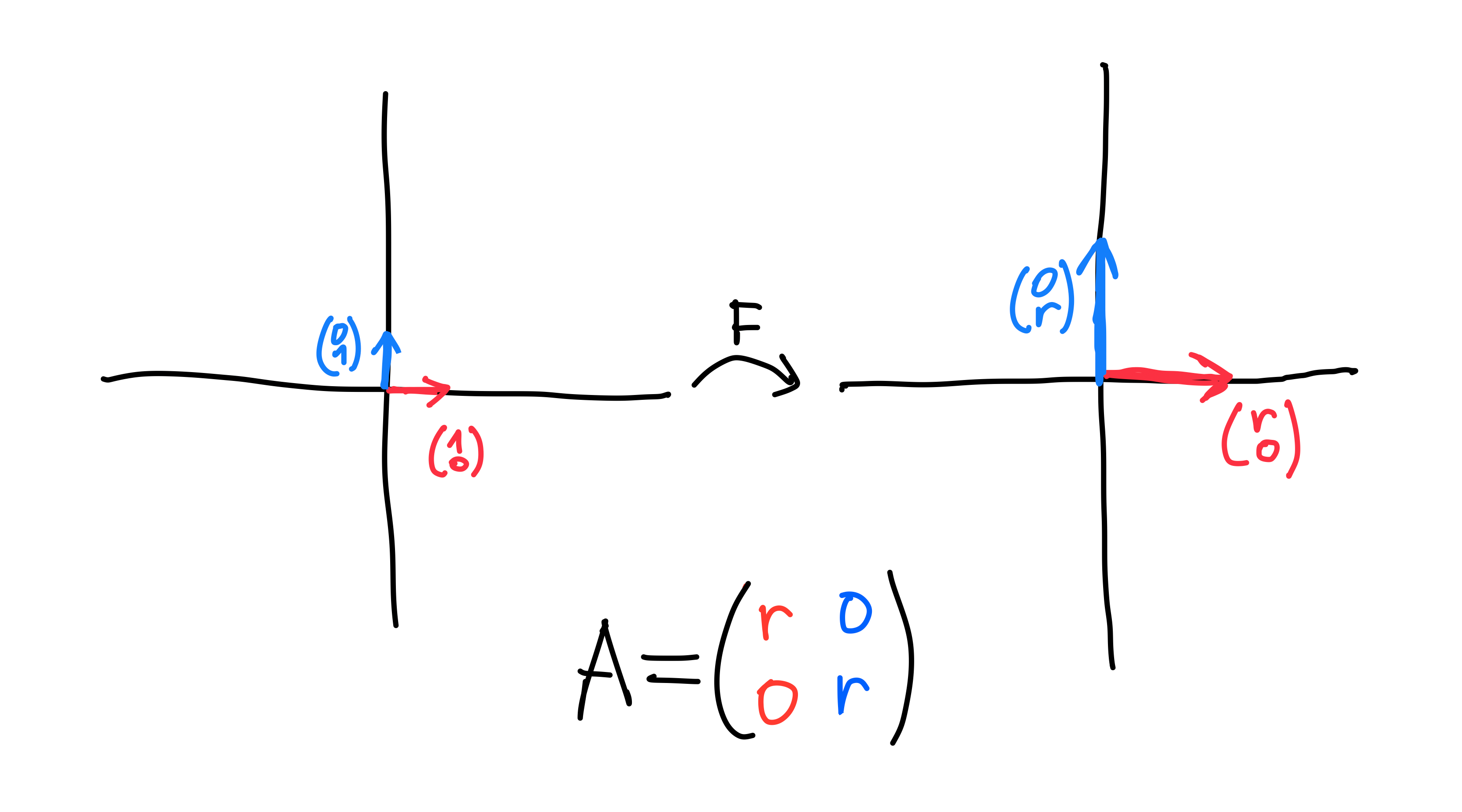
Scaling by r
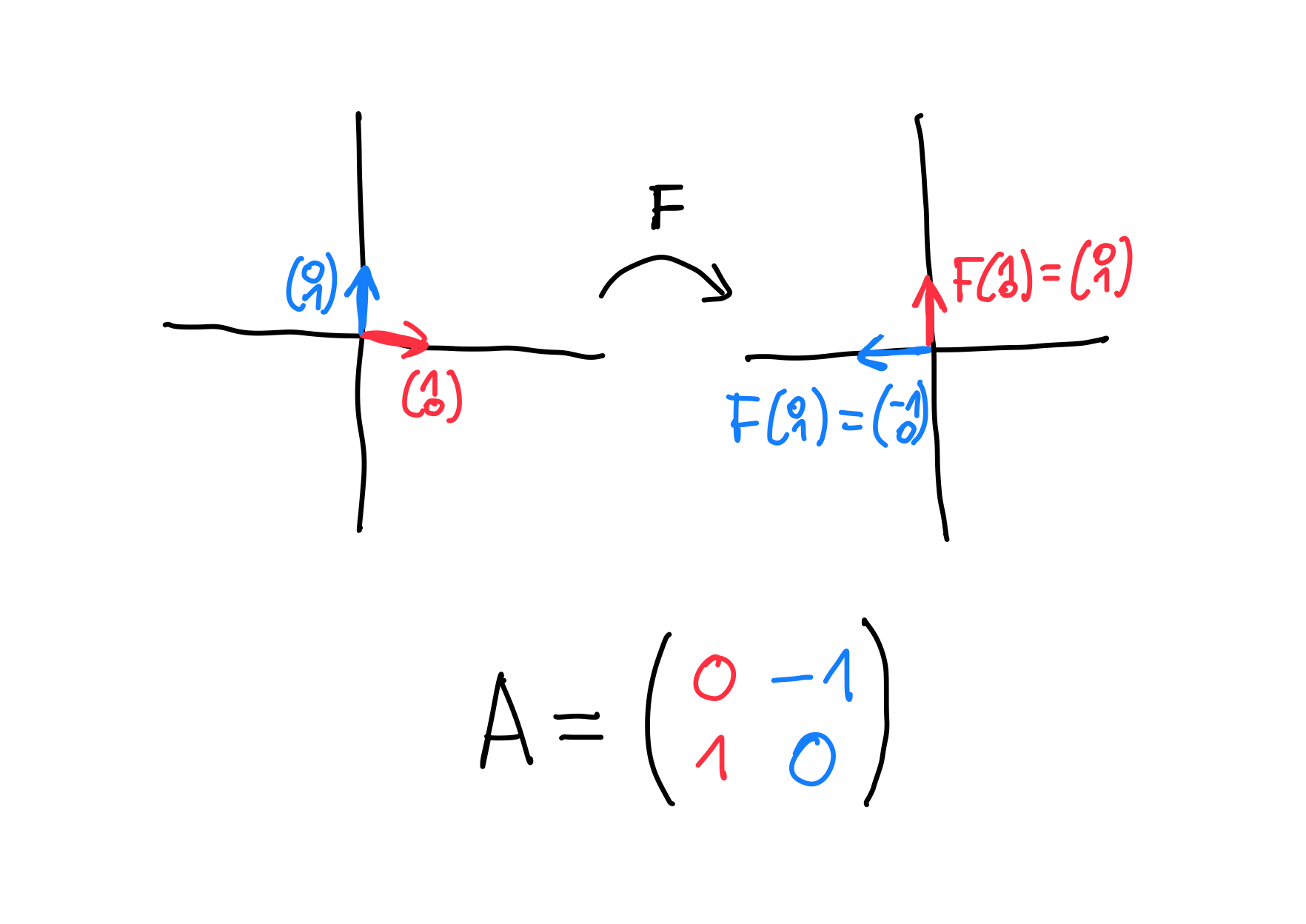
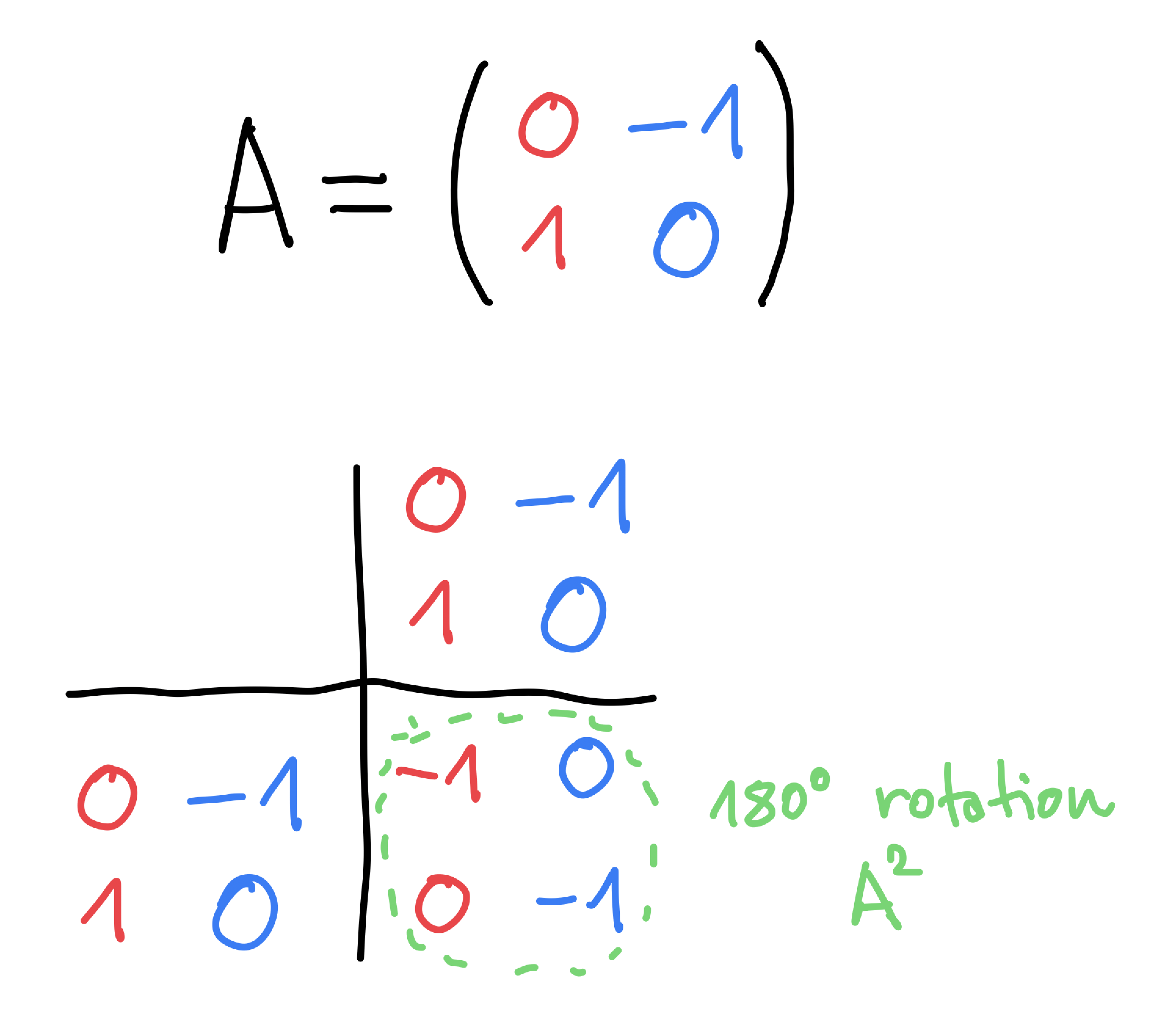
Rotation by 90°
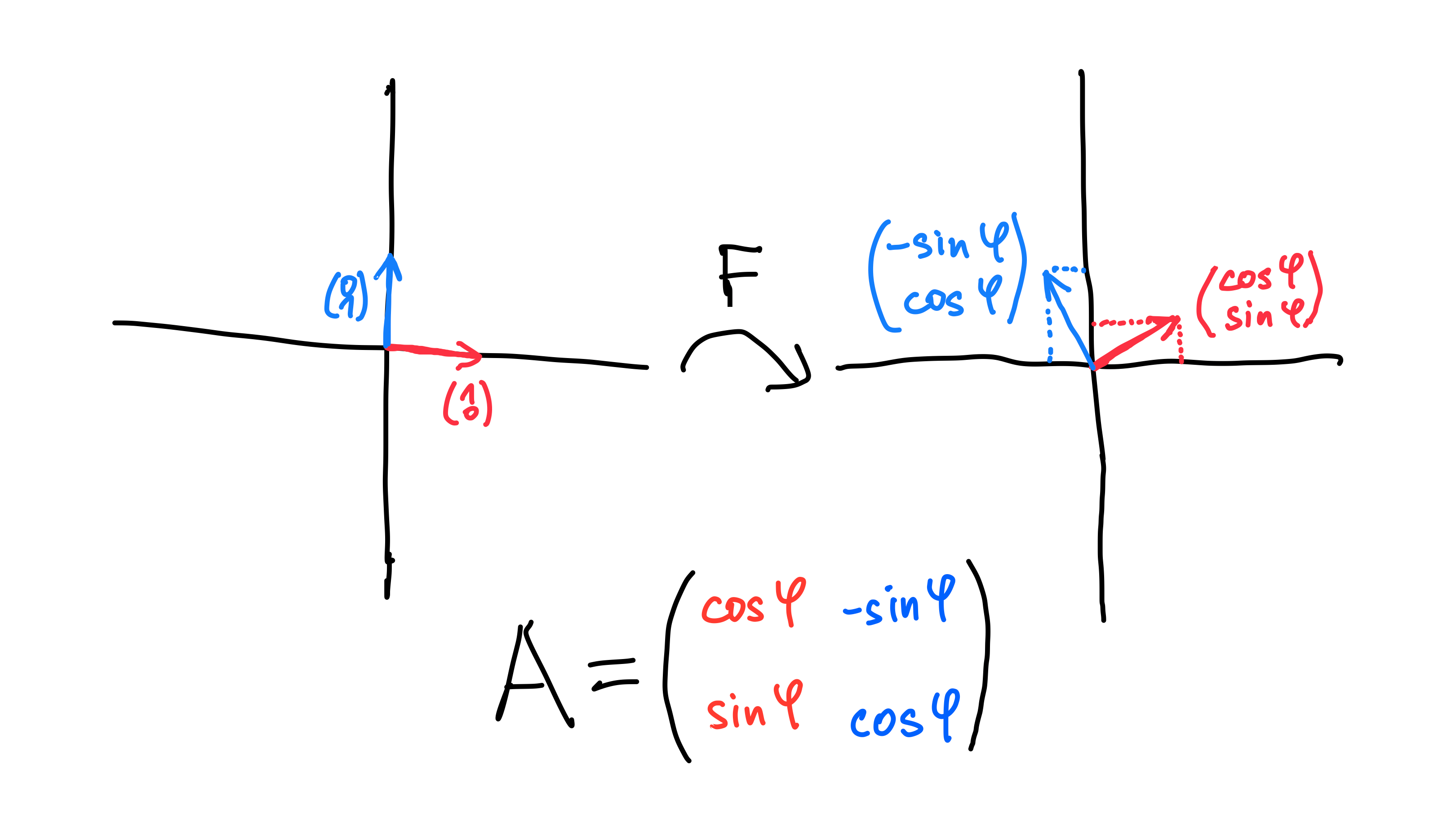
Rotation by an angle 𝜑
Mapping vectors ← matrix vector multiplication
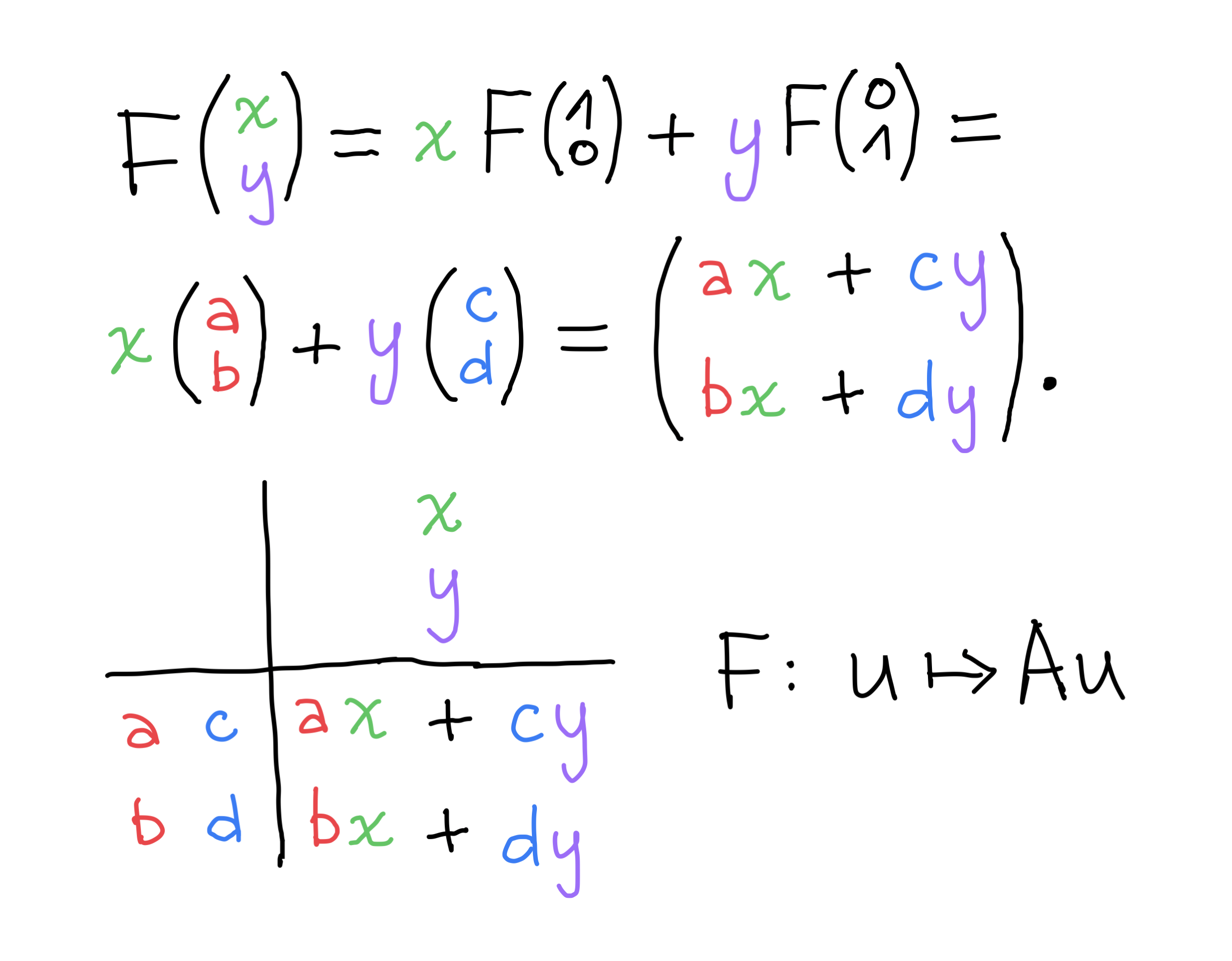
Rotating a vector by 90°
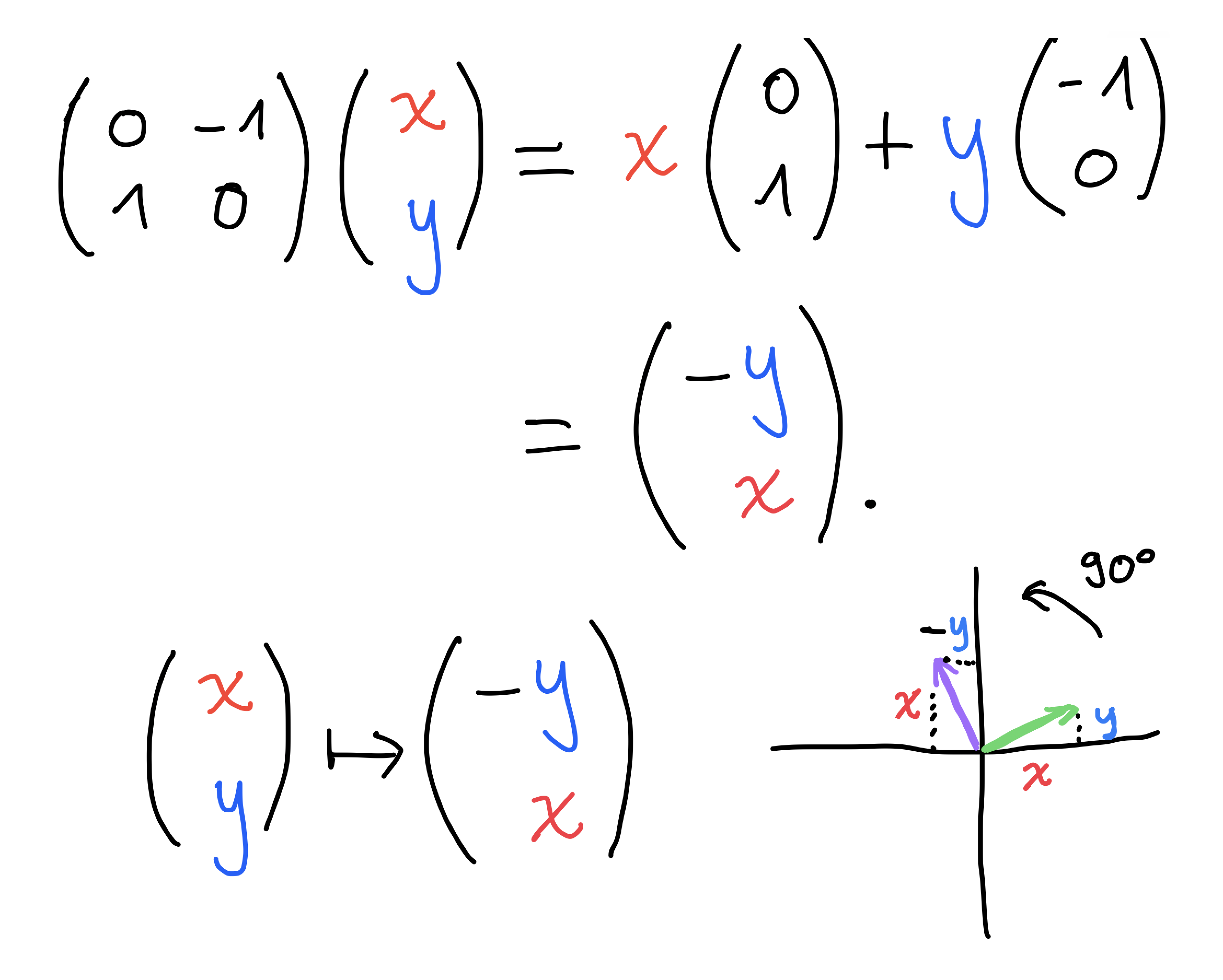
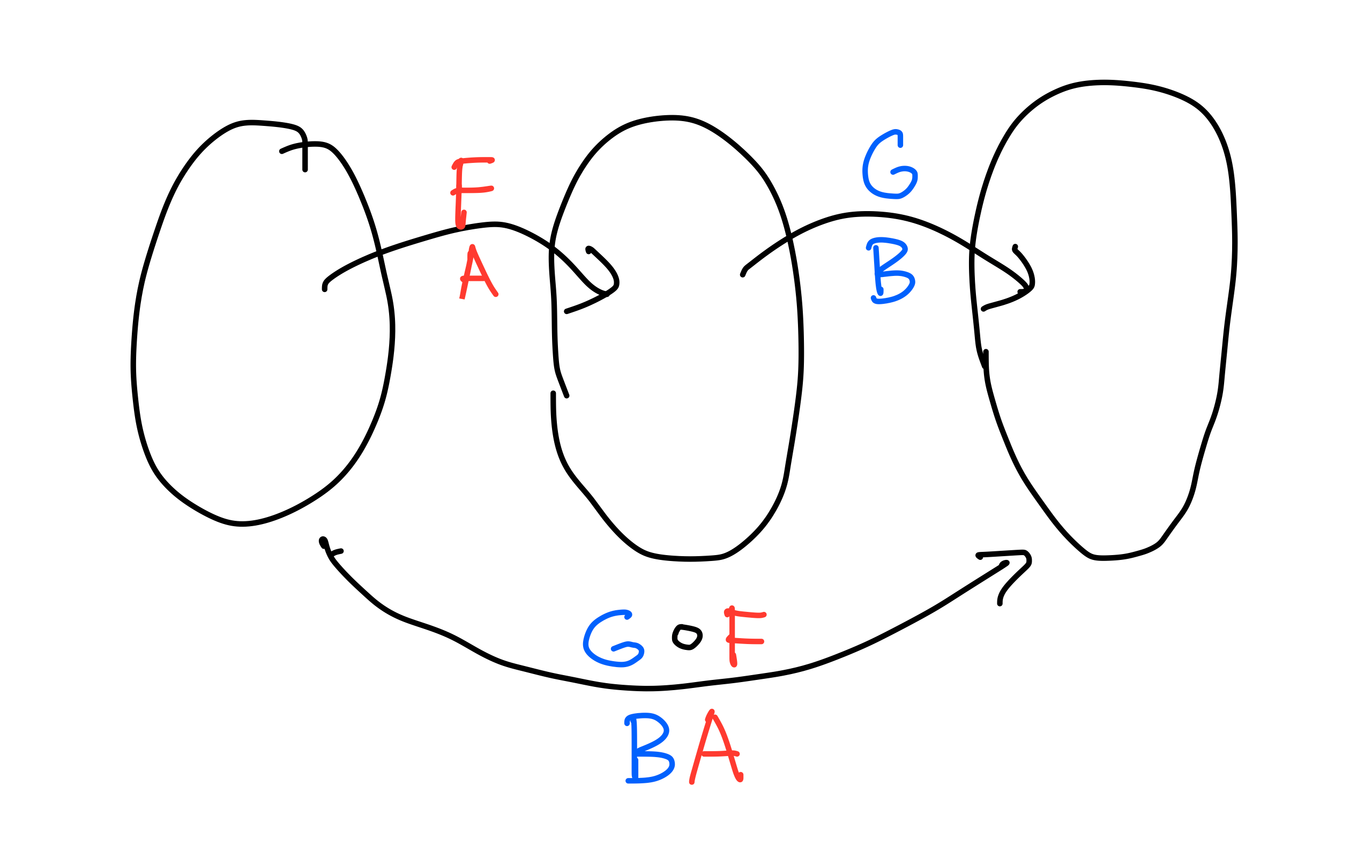
Composition ← matrix multiplication
Multiplying rotation by 90° with itself
My books about linear algebra (in Czech)
Povídání o lineární algebře
Lineární algebra II
Lineární algebra III
Geometry of complex numbers
Points of the plane
Transformations of the plane
Addition works the same
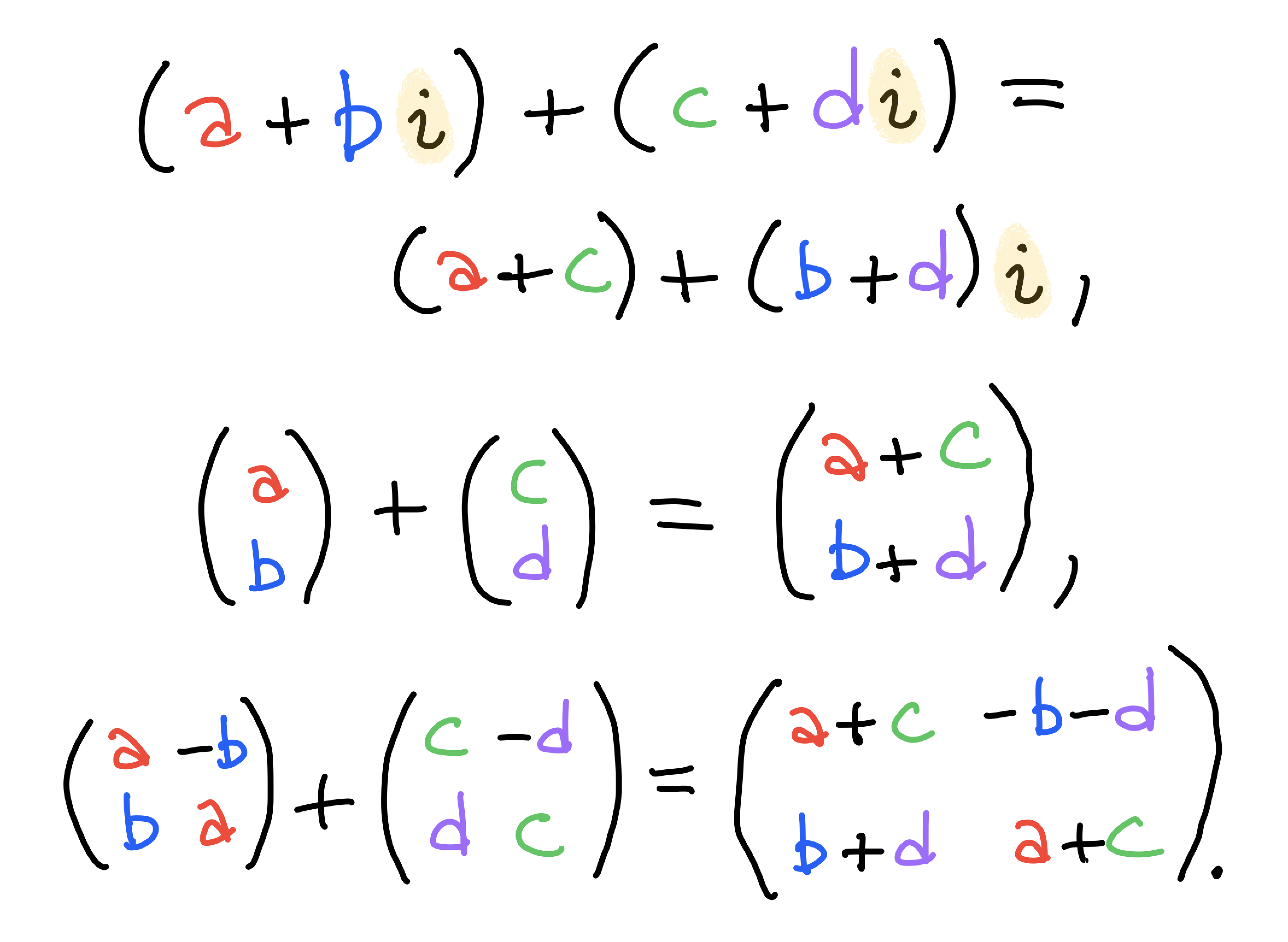
Complex multiplication
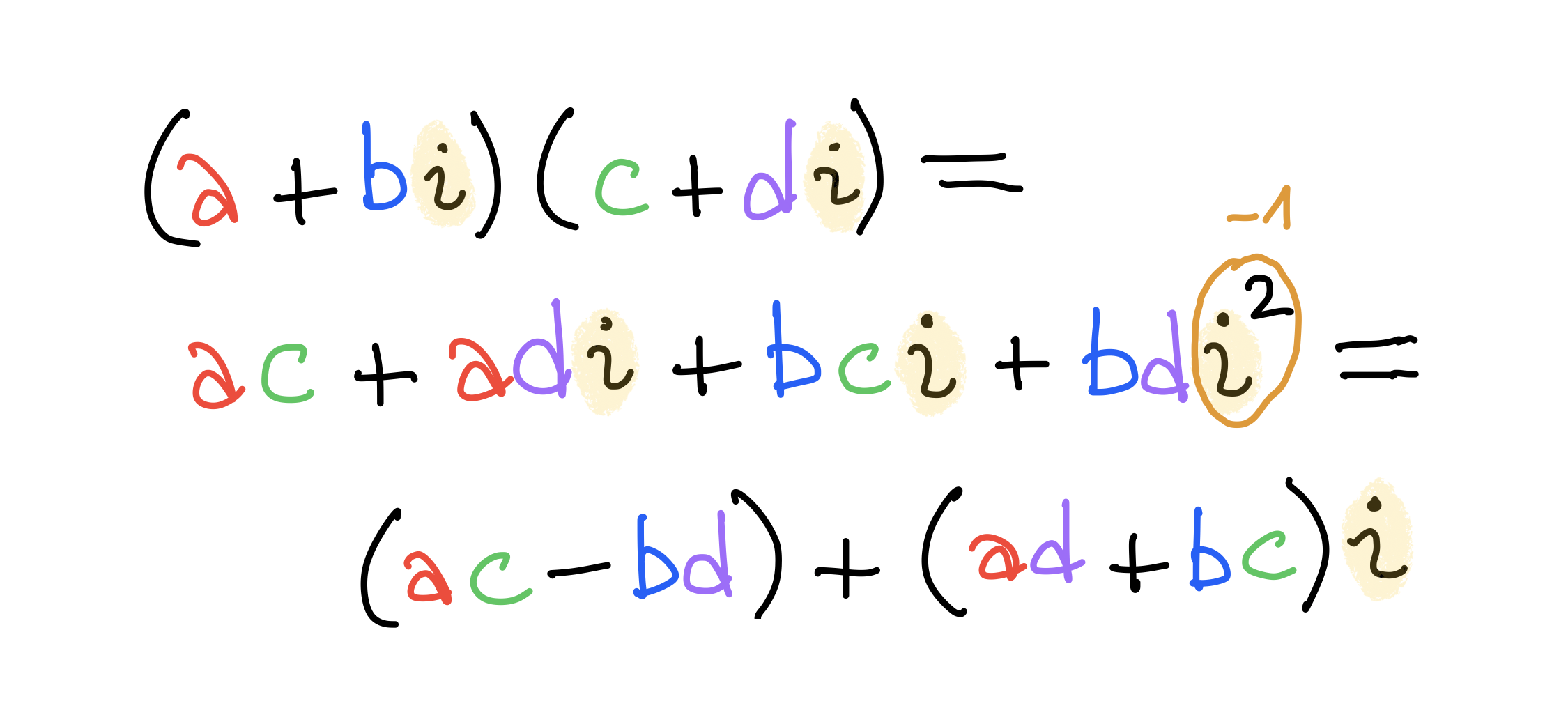
Matrix multiplication
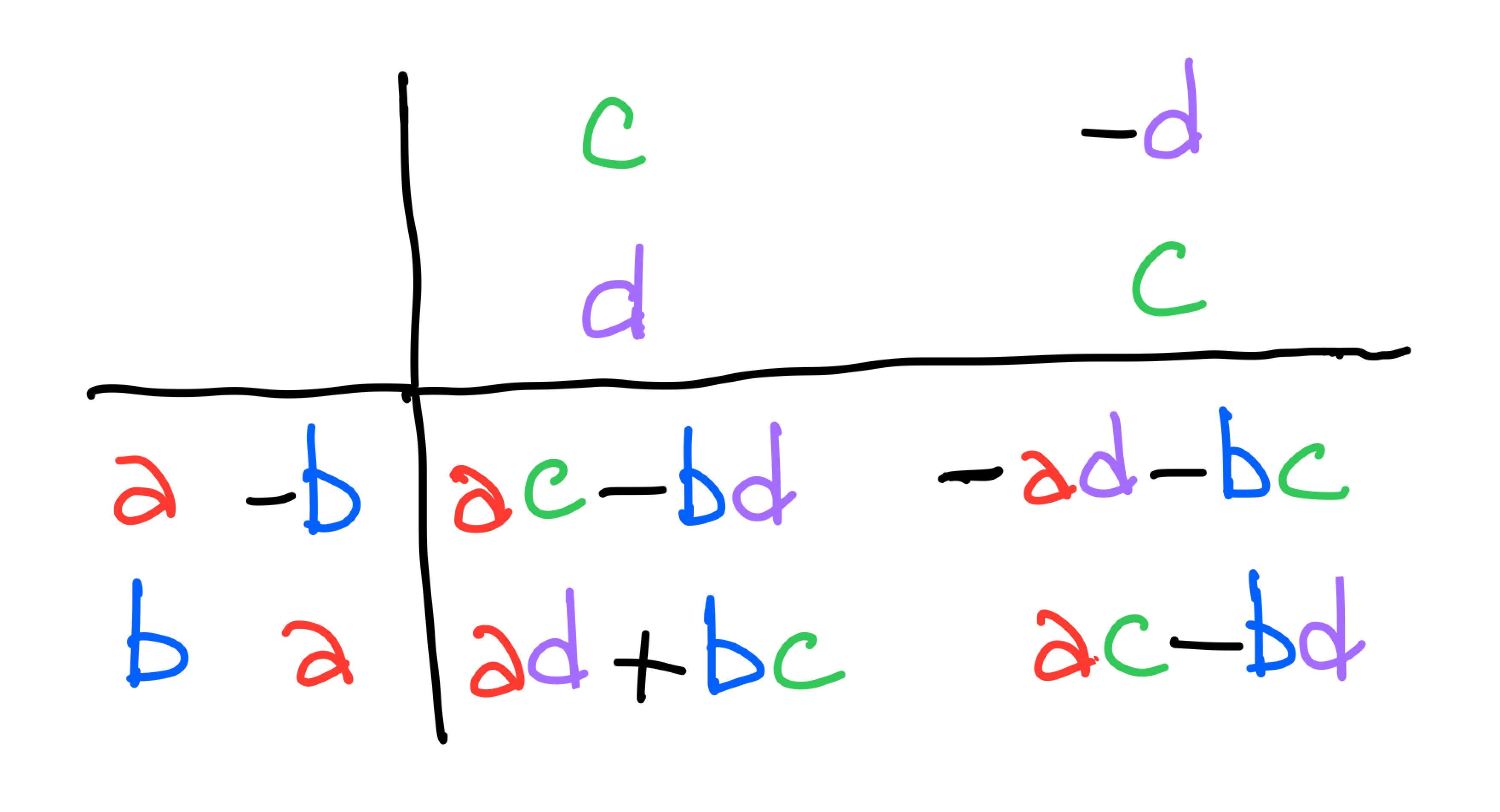
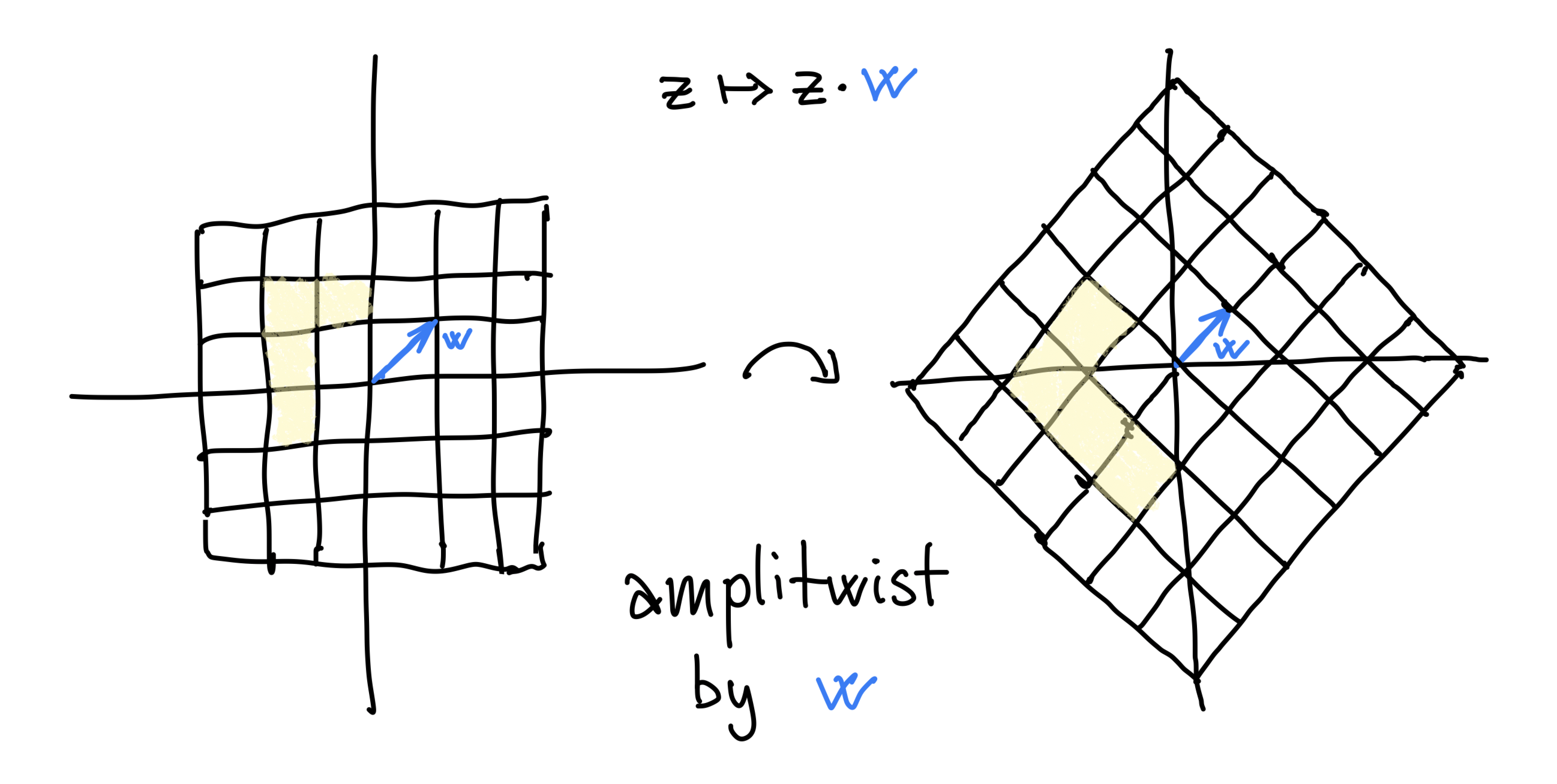
Which geometric transformation?
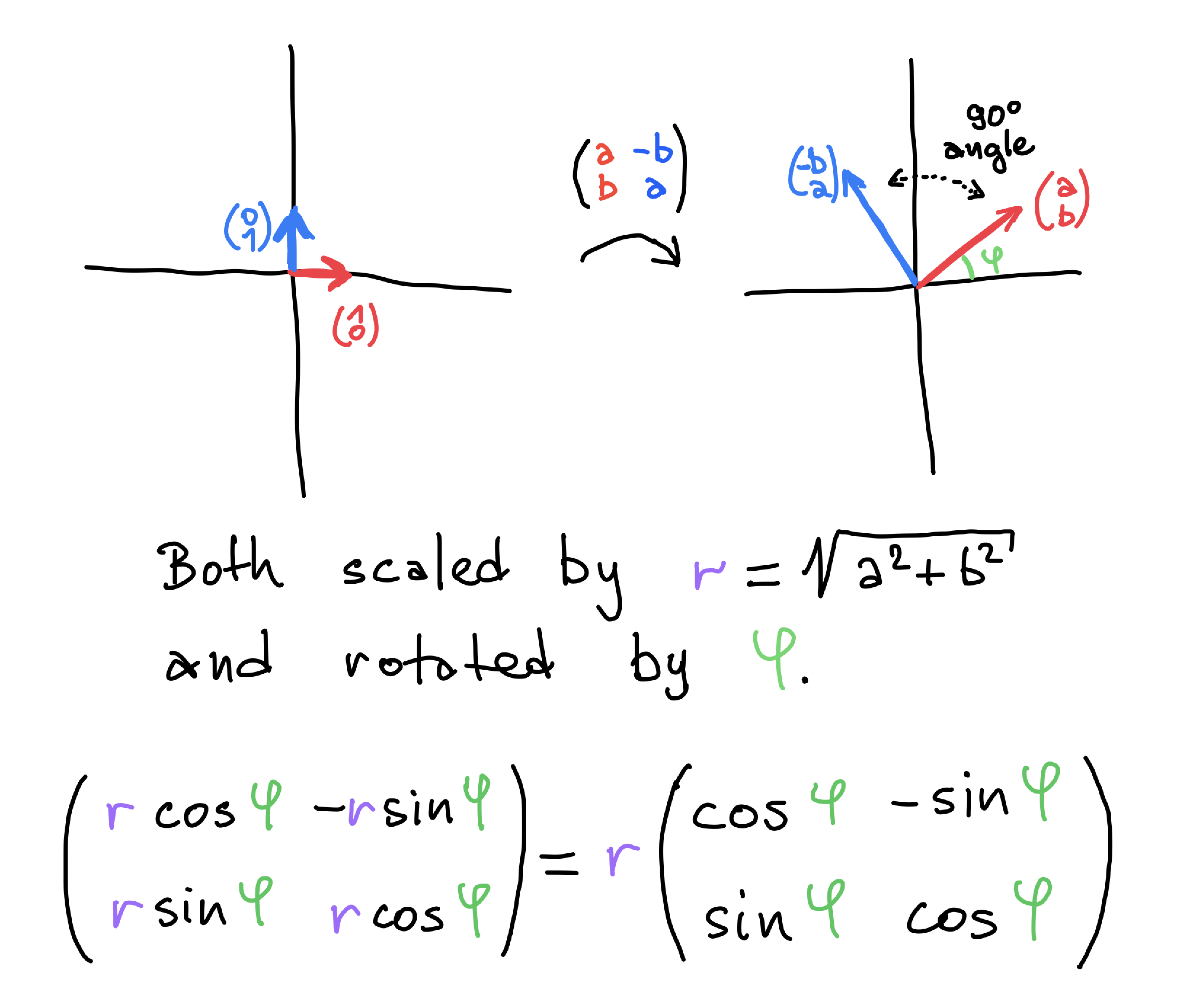
Amplitwist
Scaling + rotation =
amplification + twisting =
“amplitwist”.
Trigonometric form of complex numbers
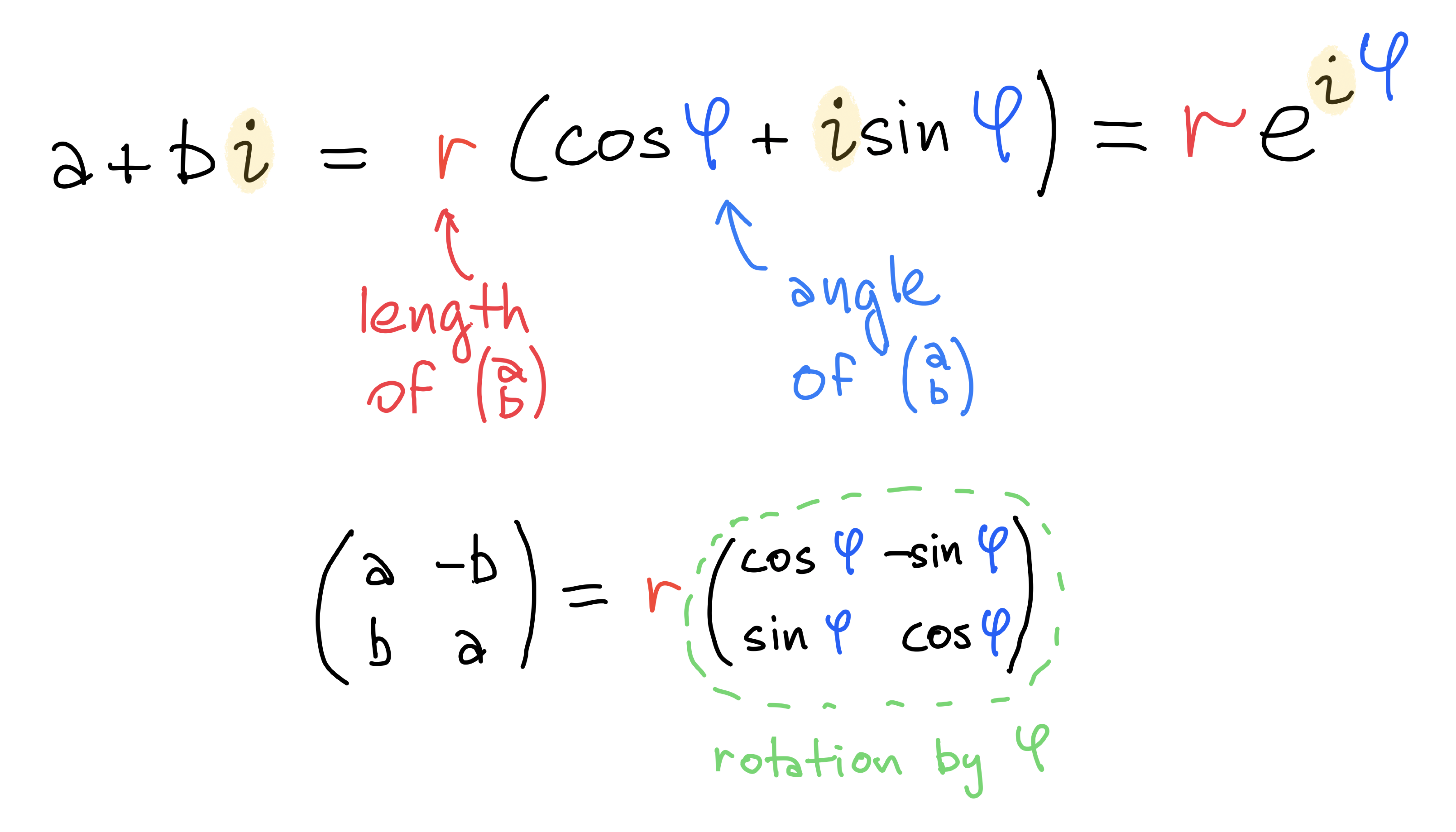
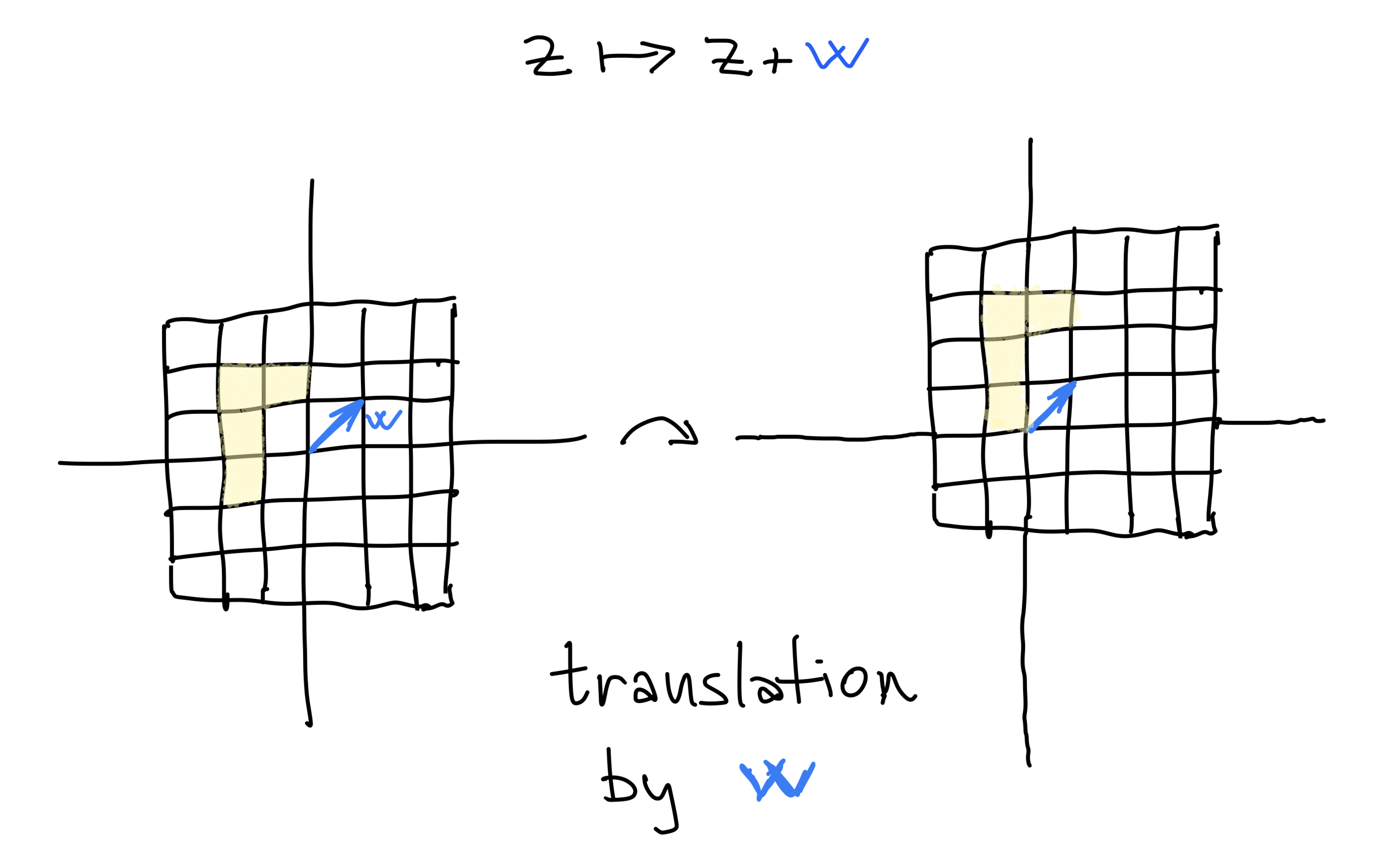
Addition is translation
Multiplication is amplitwist
Basic transformations
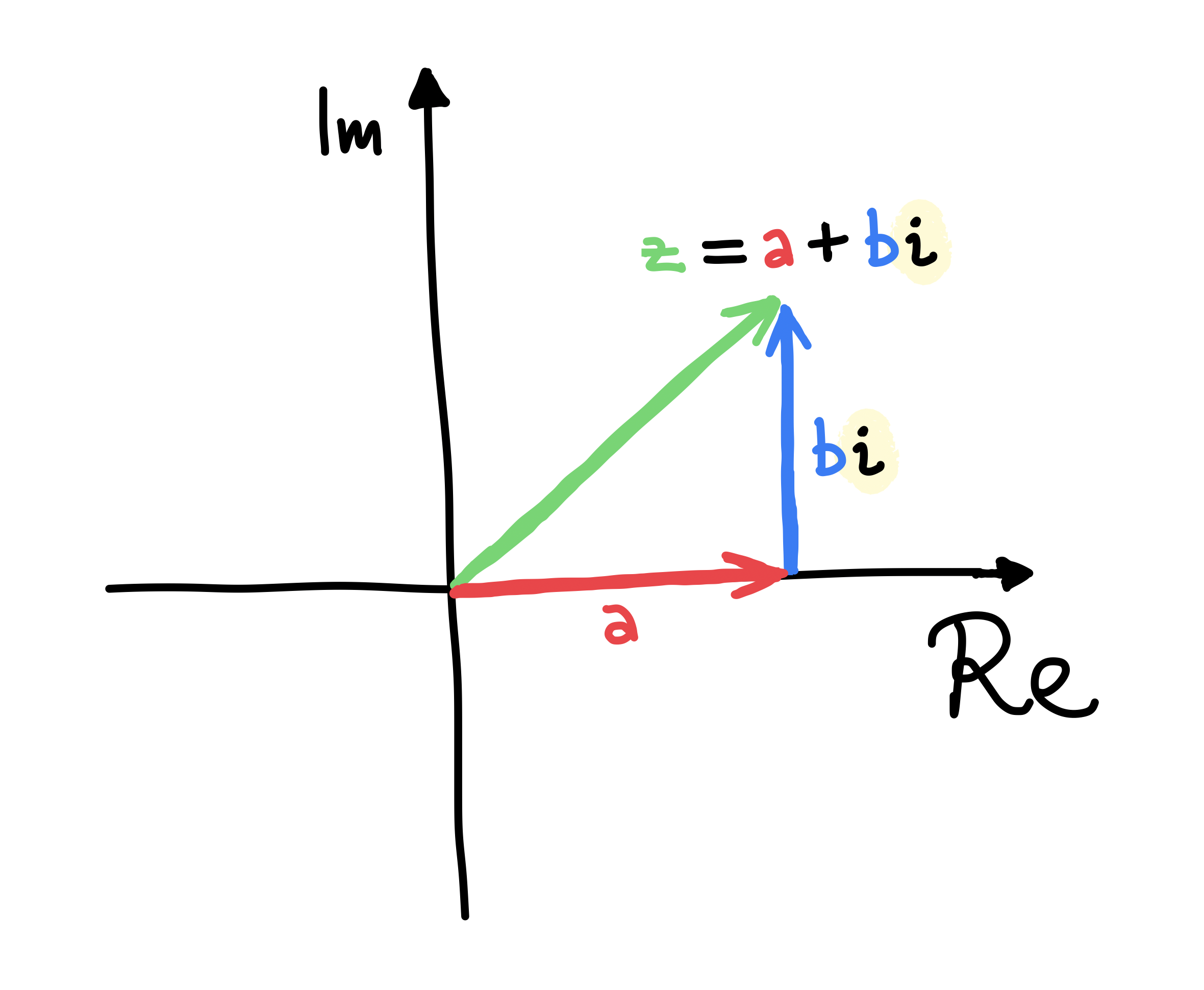
Geometric meaning of a+b𝑖
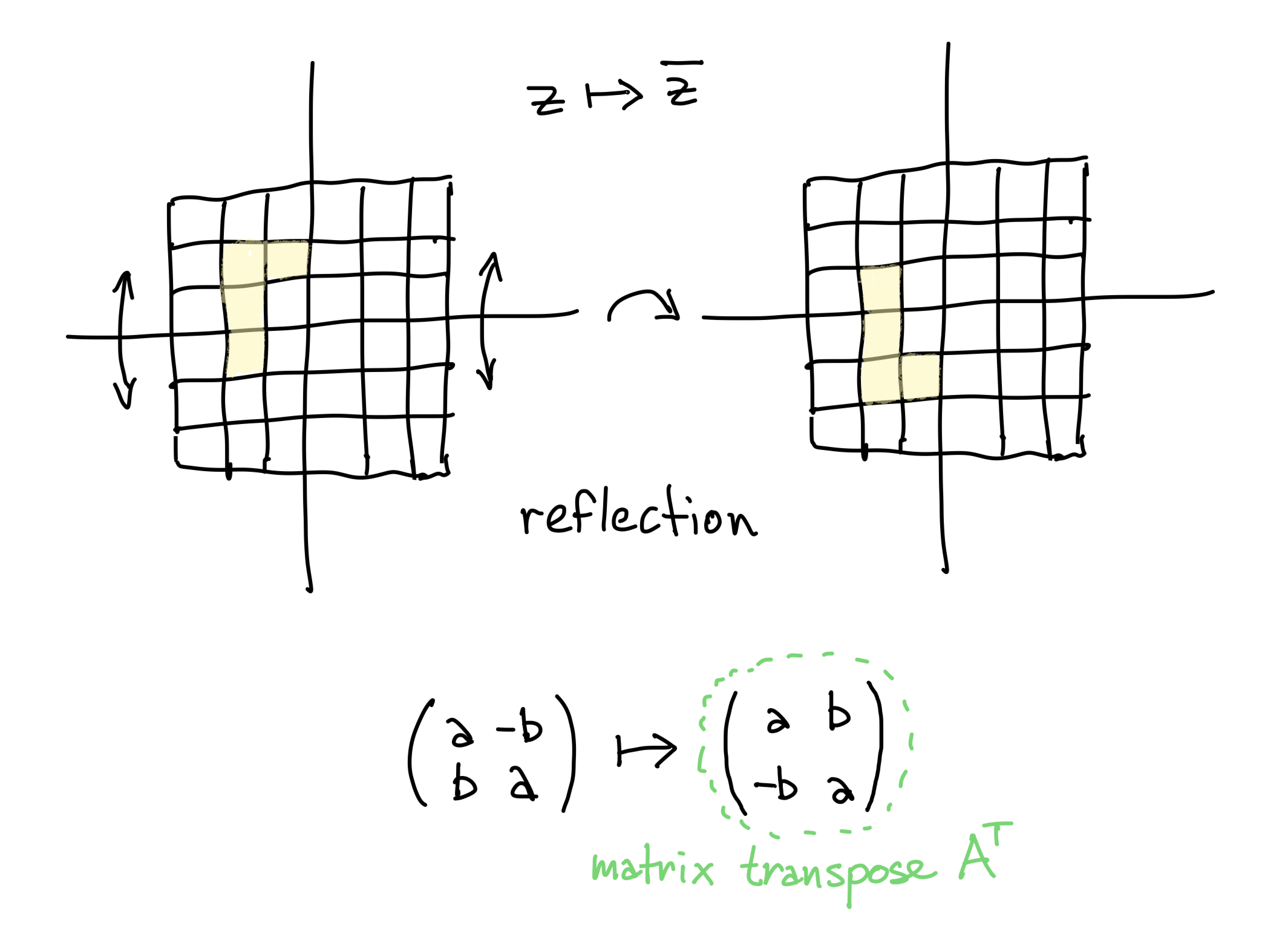
Conjugation is reflection
Möbius transformations
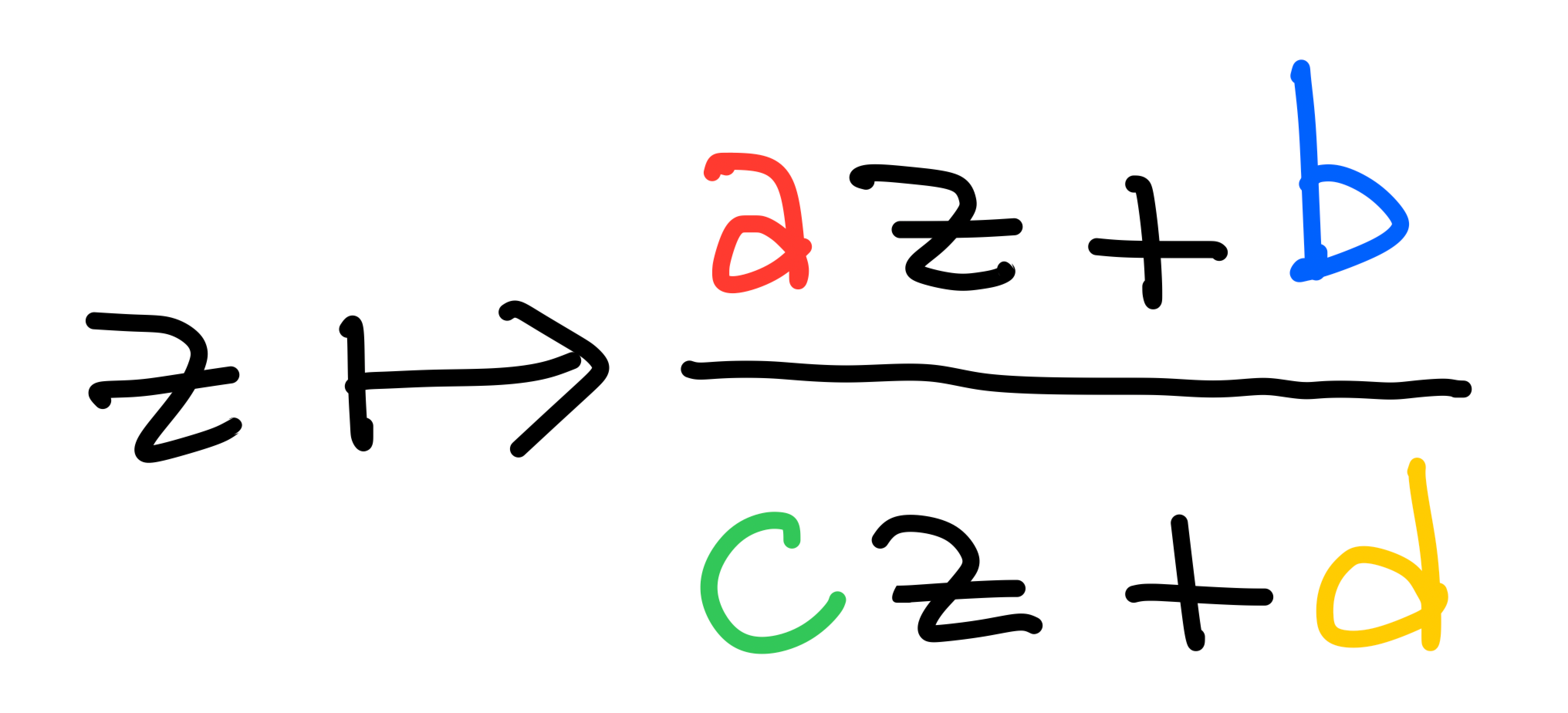
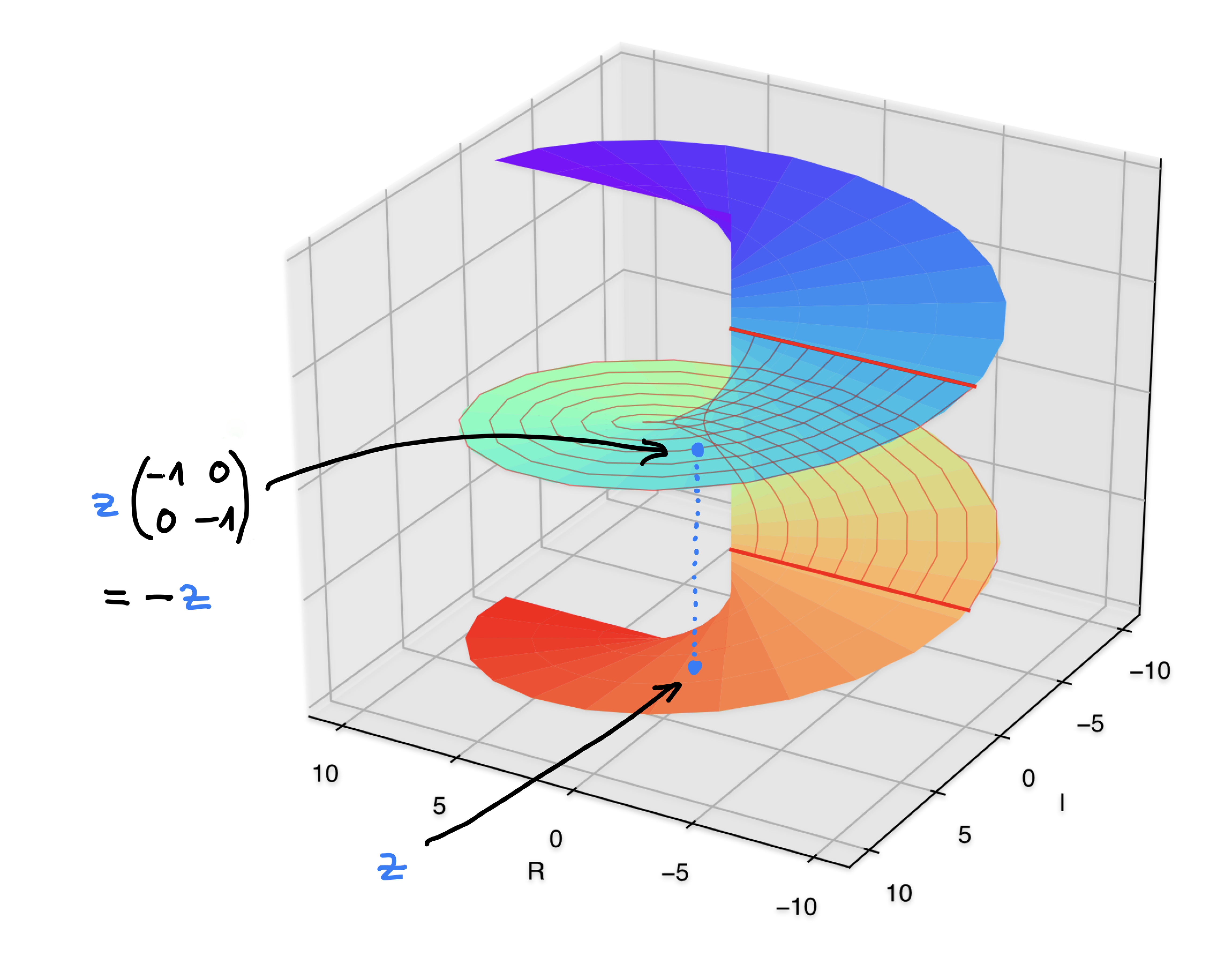
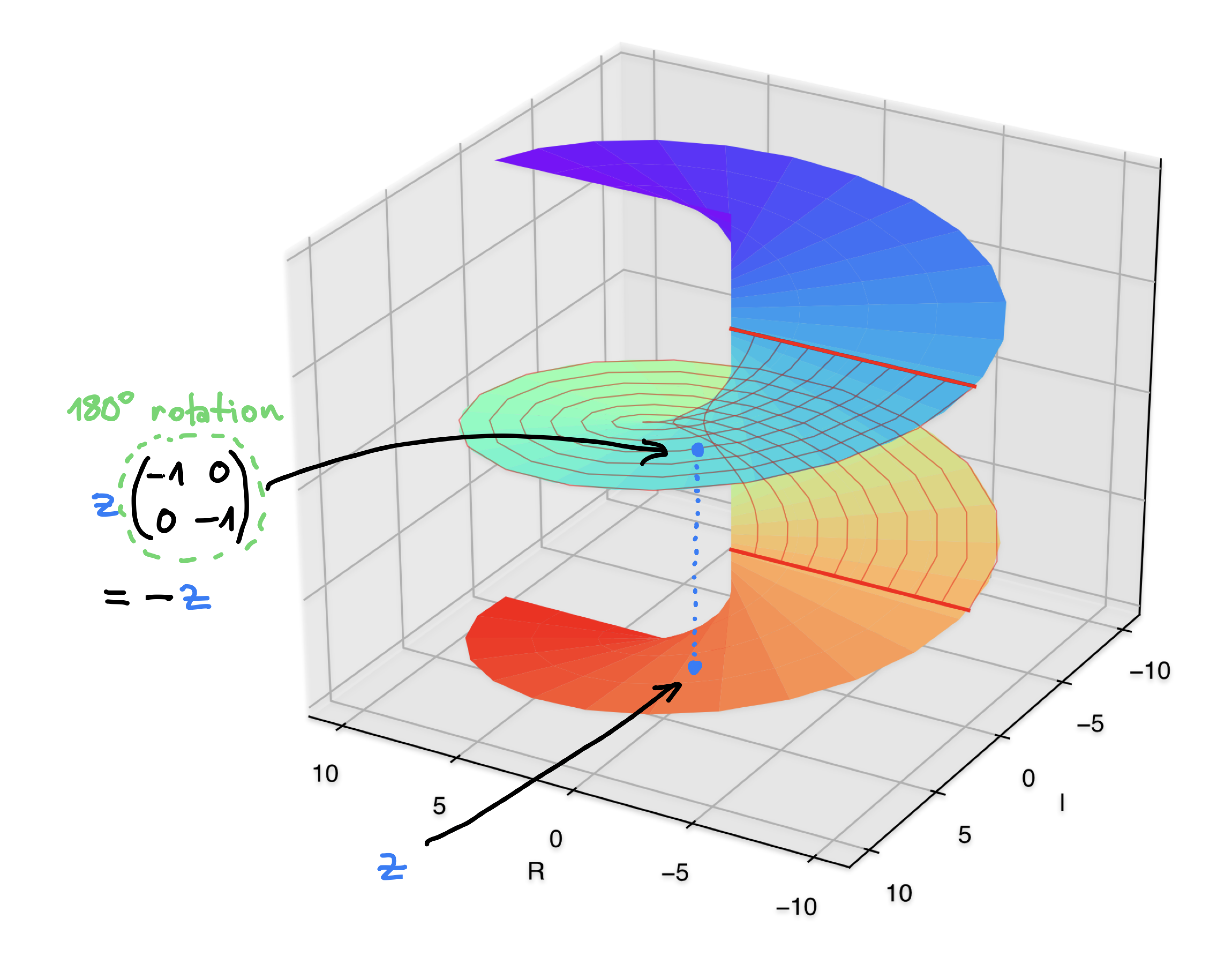
Geometric meaning of the square transformation
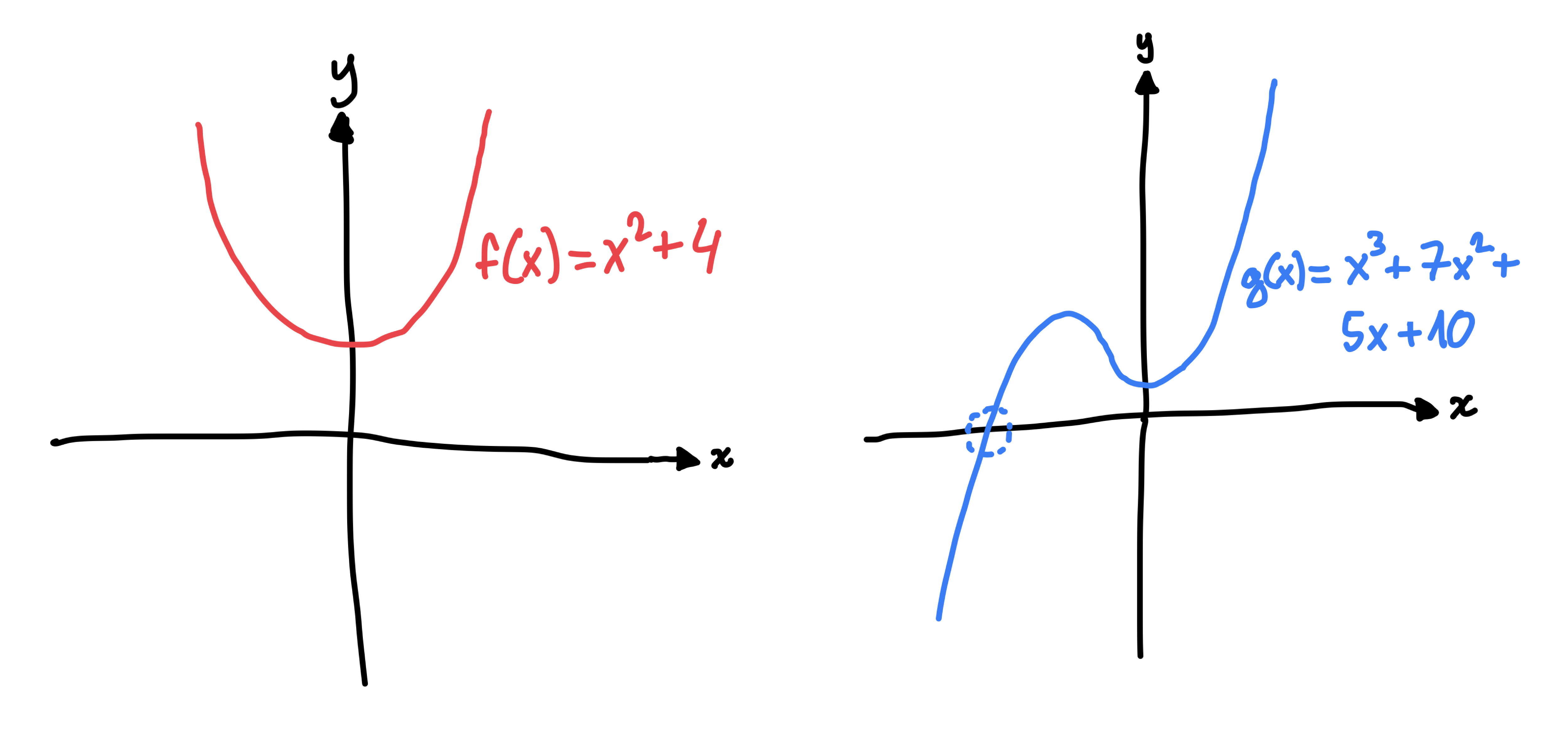
Geometry of x ↦ x²
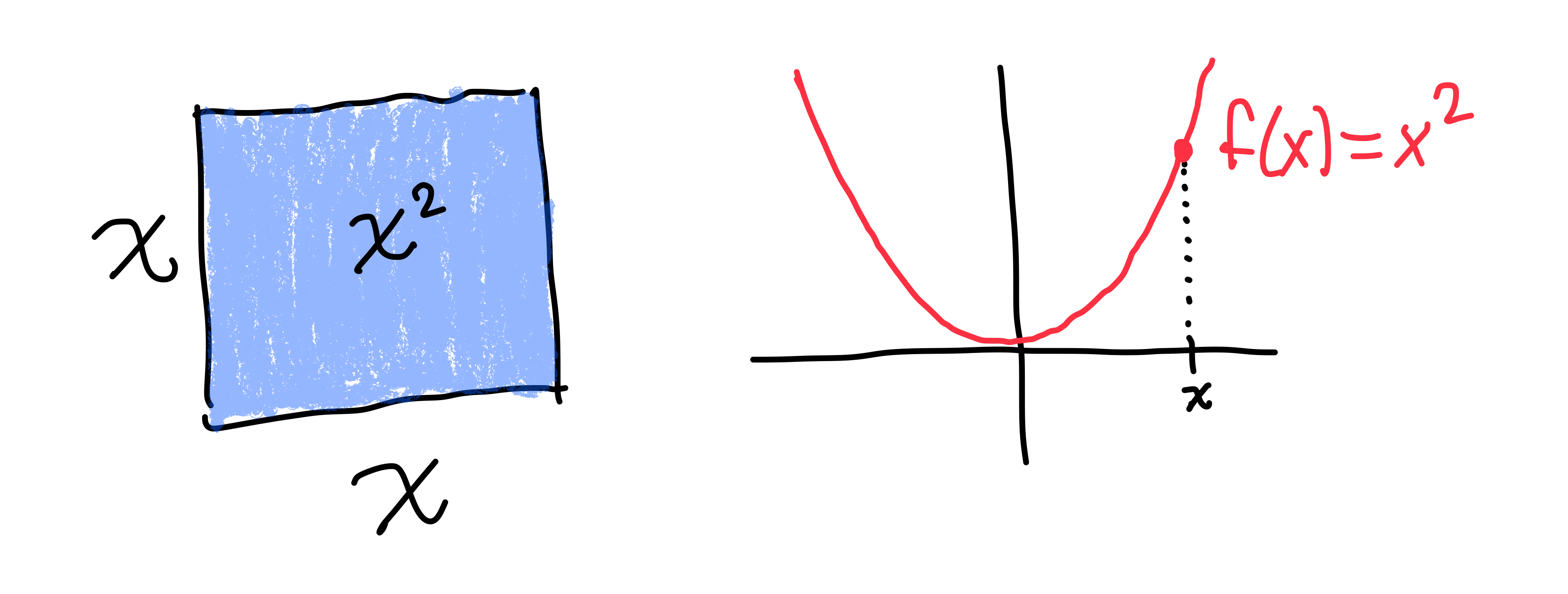
Geometry of z ↦ z²
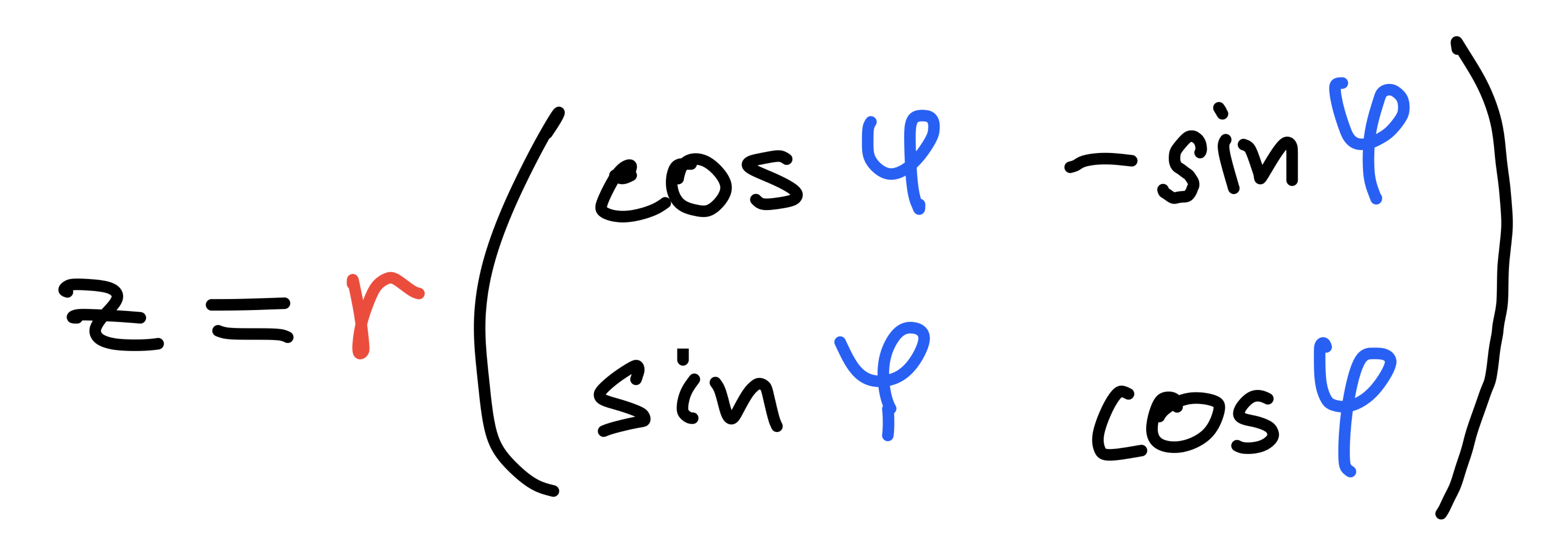
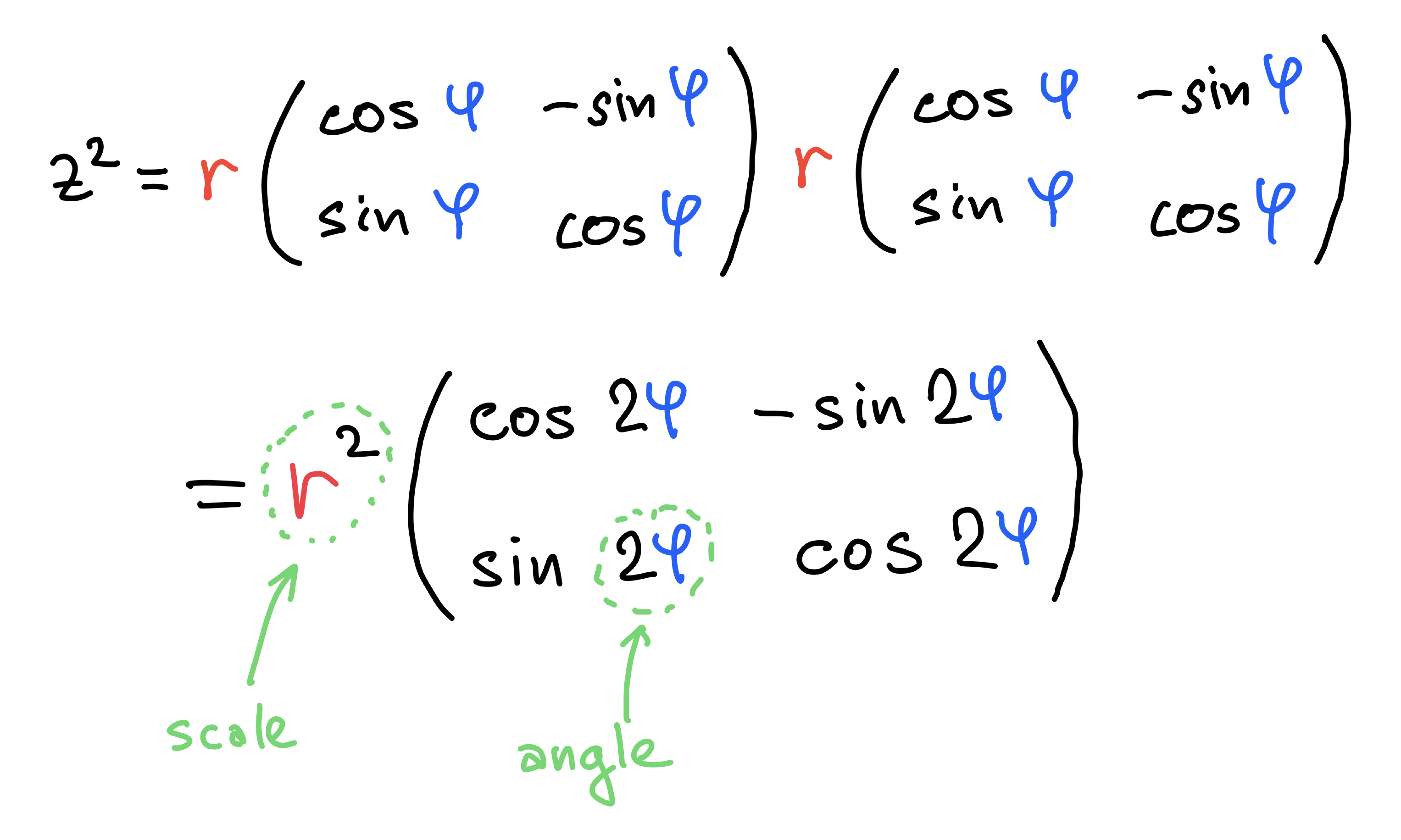
Or visually
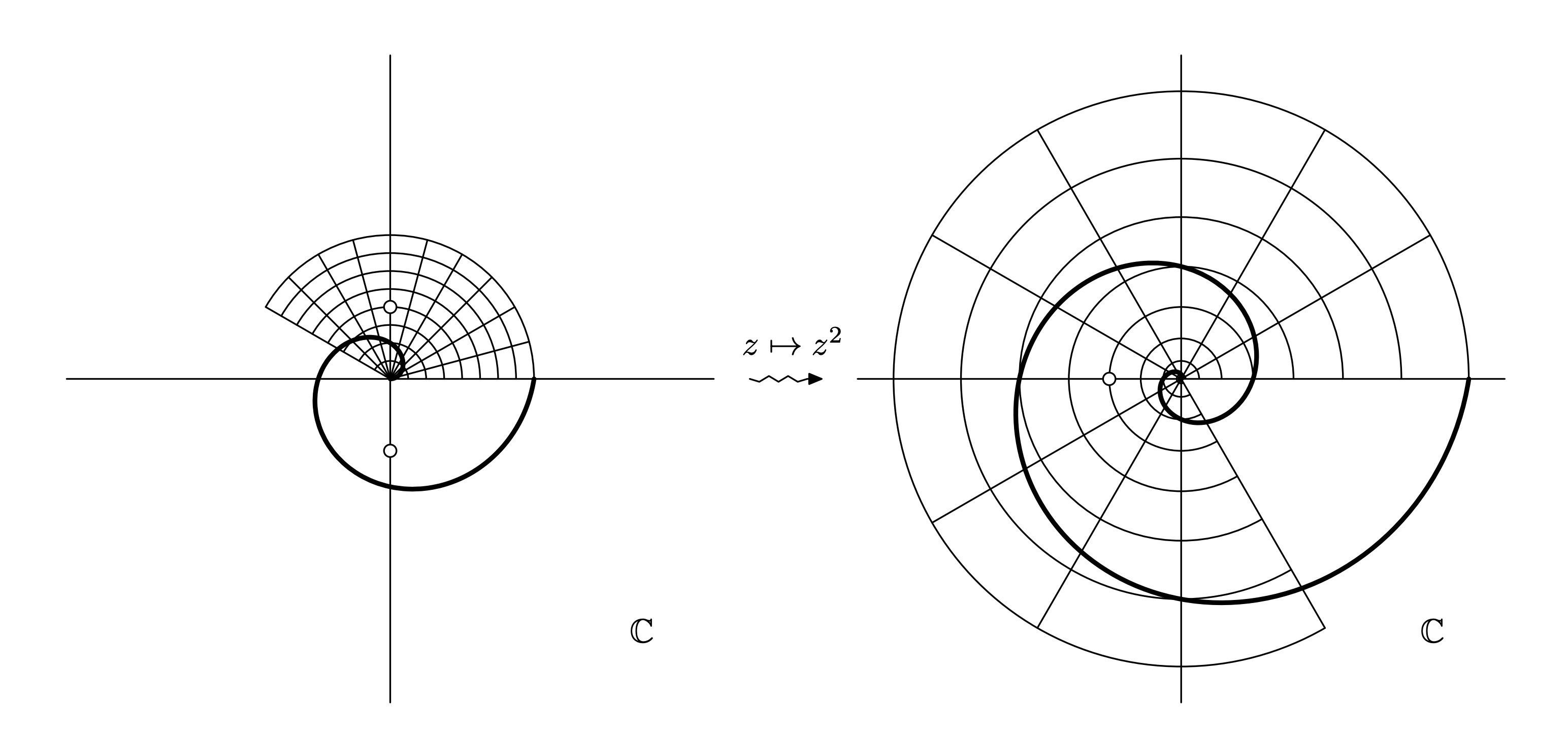
Same symbols, different meaning 🙁
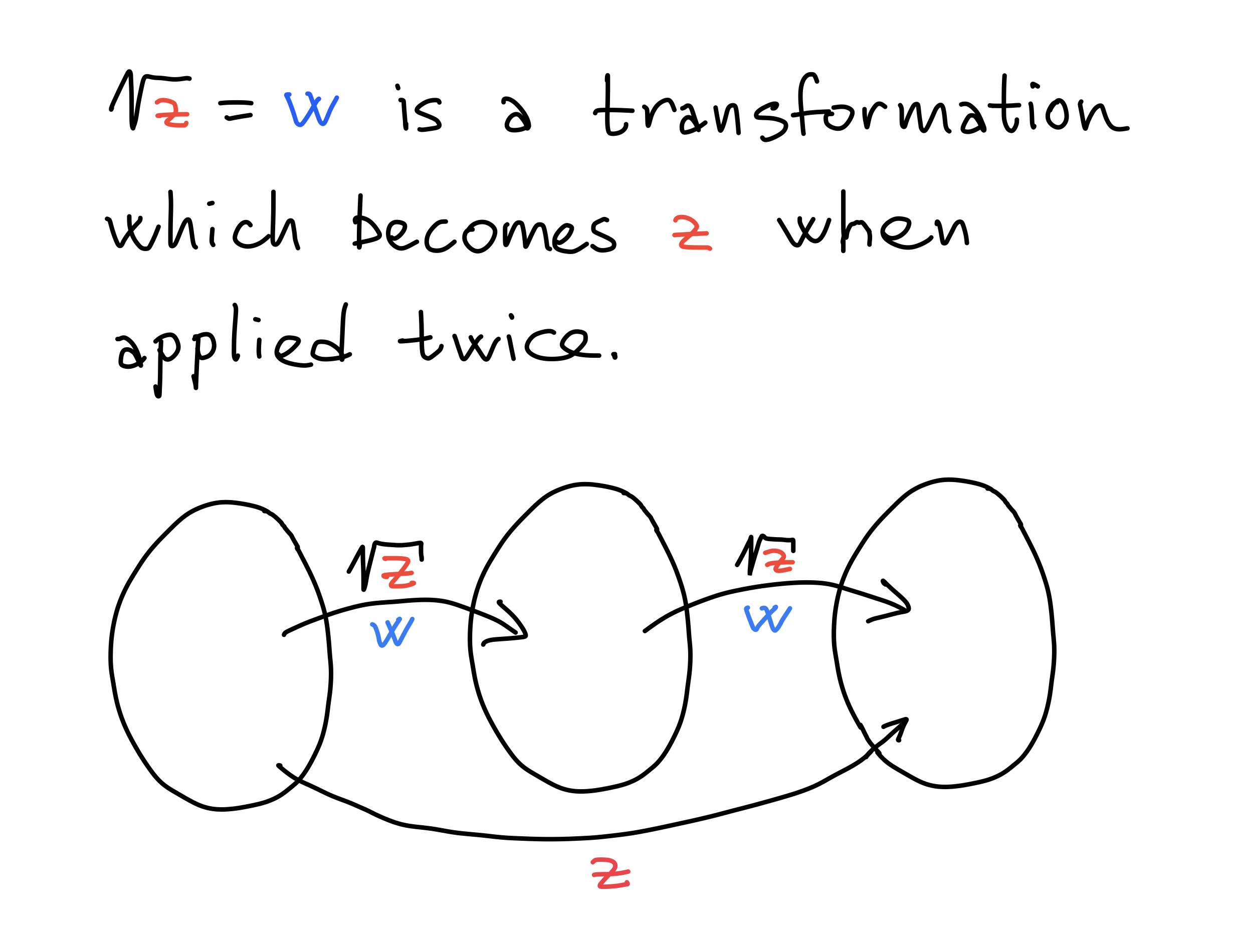
What is √ ?
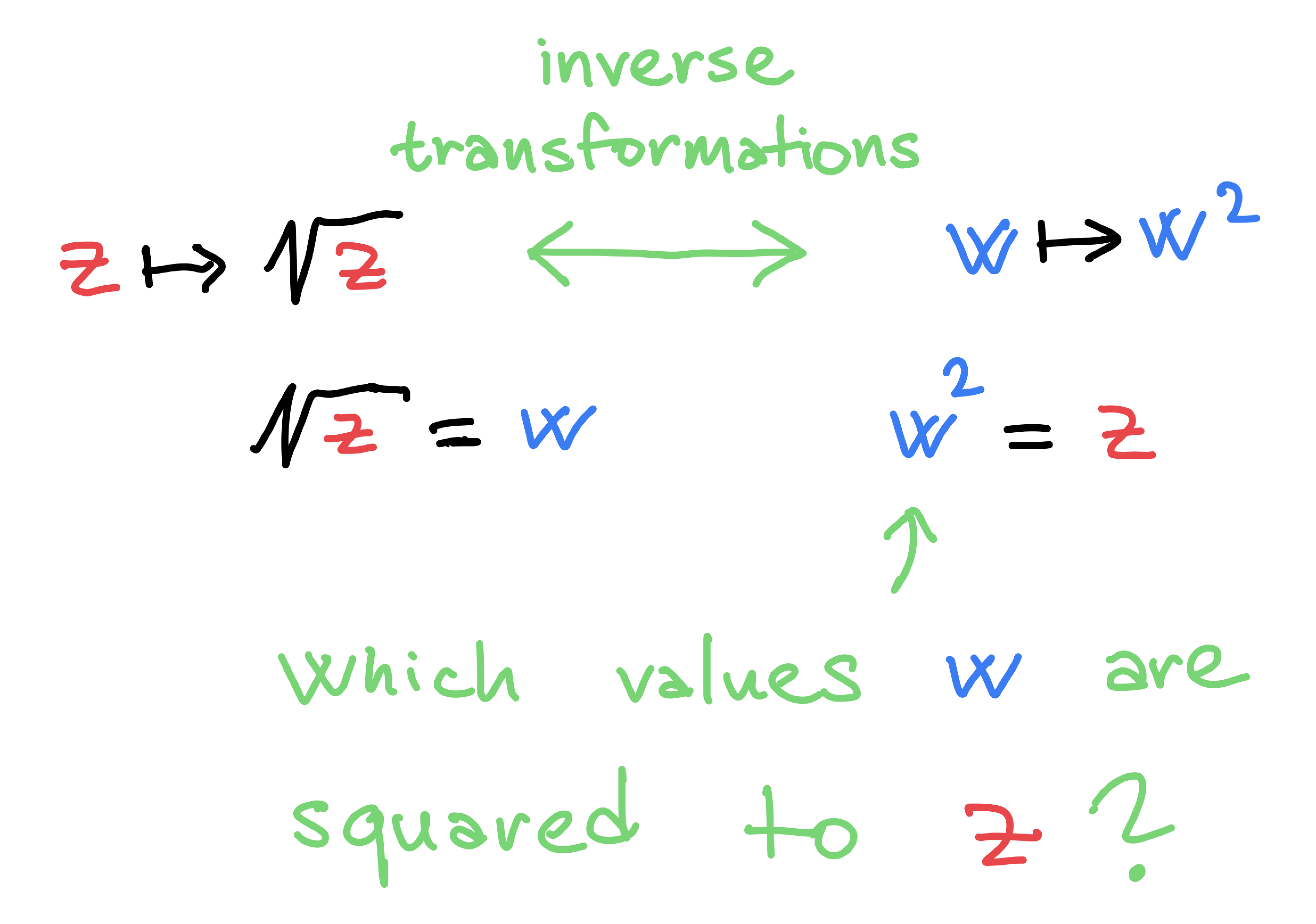
Geometric meaning of √z
√-1
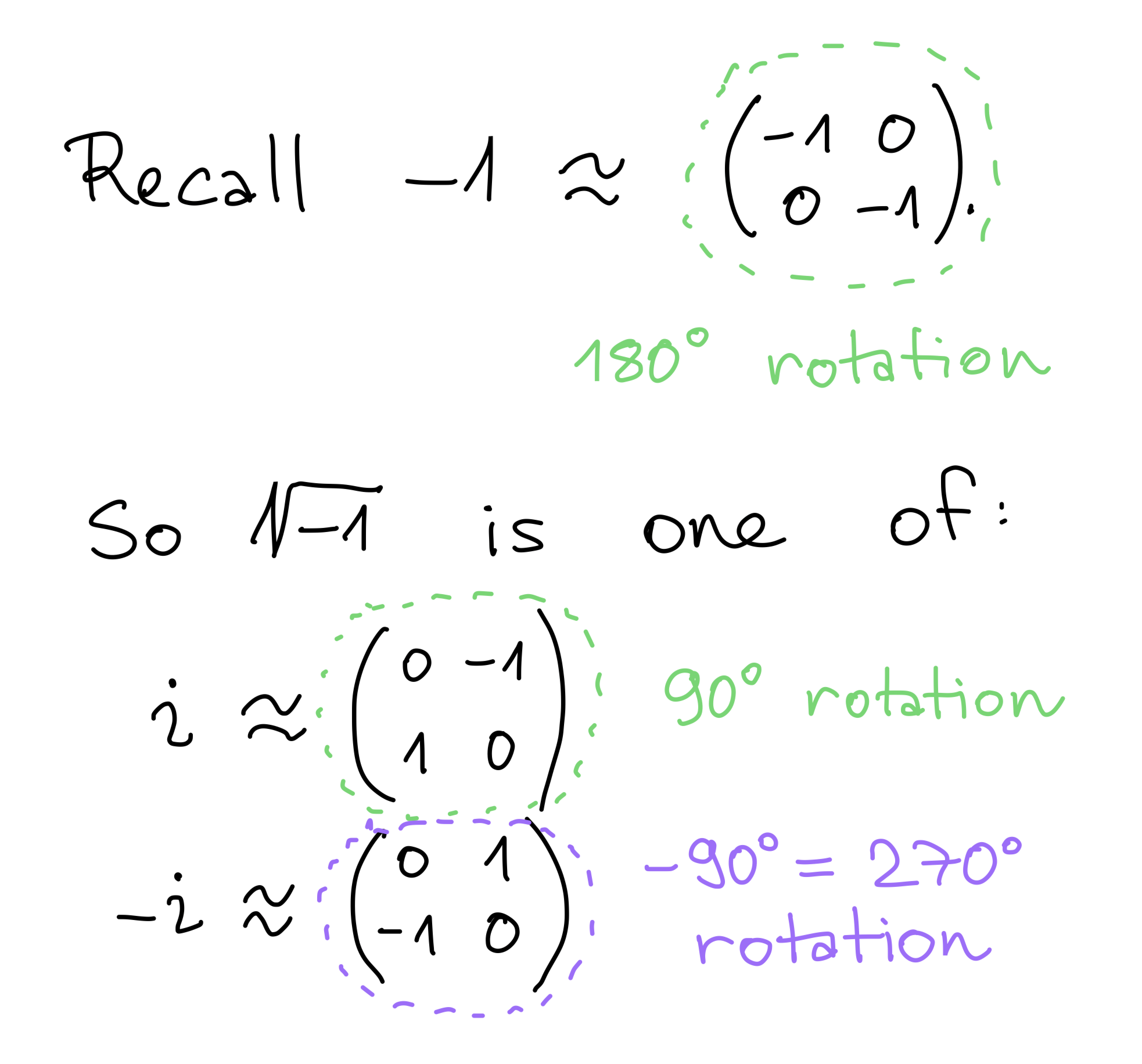
√z
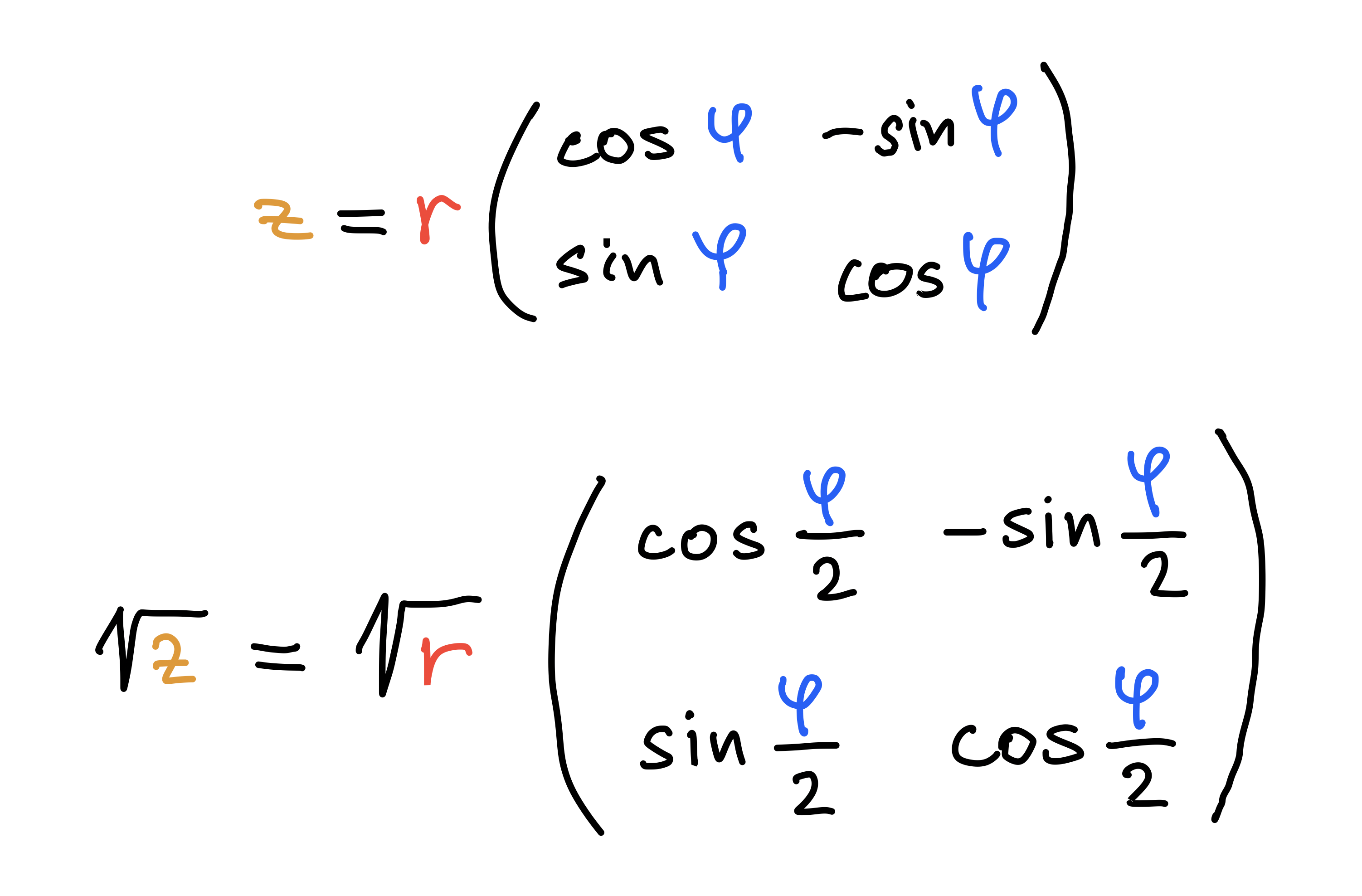
The other value of √z
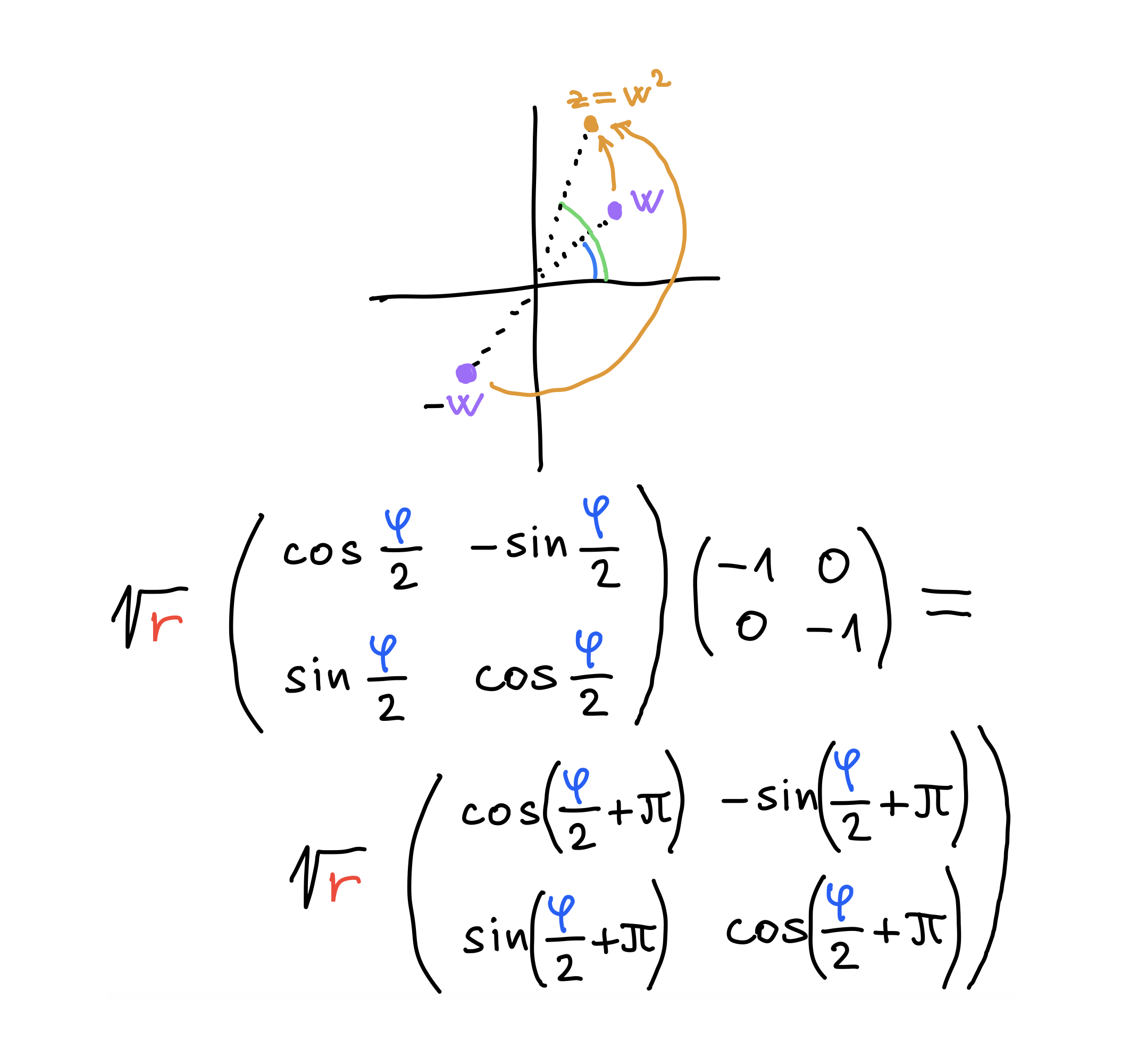
Zdeněk Hedrlín
“Complex analysis is the study of sinks and vortexes.”
Source / sink
Vortex
Juan Carlos Ponce Campuzano: Complex Analysis
complex-analysis.com
Studied brain for 40 years
OrgPad
Zero's Escape
Dice puzzle
OrgPad document about the dice puzzle
How to build understanding
Throw all ideas right in front of you
Play with them
Profit 🤑
Thinking is captured faithfully
While playing you improve understanding of your brain
20% off
SOME3
Two amazing math jokes
Why Romans sucked in algebra?
Because X was always ten.
Why Mayans counted in the base-20 numeric system?
Because they did not wear shoes.
Thanks for watching!
Sources
Complex analysis: A Visual and Interactive Introduction by Juan Carlos Ponce Campuzano, licenced under CC BY-NC-SA 4.0, available at https://complex-analysis.com/
Dice Puzzle video: https://www.youtube.com/watch?t=900s&v=QSl2vqr4BV4
Girolamo Cardano. Stipple engraving by R. Cooper., licenced under CC-BY 4.0, available at https://en.wikipedia.org/wiki/Gerolamo_Cardano#/media/File:Girolamo_Cardano._Stipple_engraving_by_R._Cooper._Wellcome_V0001004.jpg
Village Ambiance by Alexander Nakarada, licenced under CC-BY 4.0 (https://filmmusic.io/standard-license), available at https://filmmusic.io/song/6586-village-ambiance
