What is 1ᵏ+2ᵏ+⋯+nᵏ?

Created by Pavel Klavík

Sums involving integers and their powers were studied for thousands of years. This OrgPage explores the general pattern: a sum of a polynomial of degree d from 1 to n is another polynomial of degree d+1 evaluated at n. An elegant proof hidden within Pascal's triangle is revealed.

Sum of polynomials is a polynomial

1+2+3+4+⋯+n

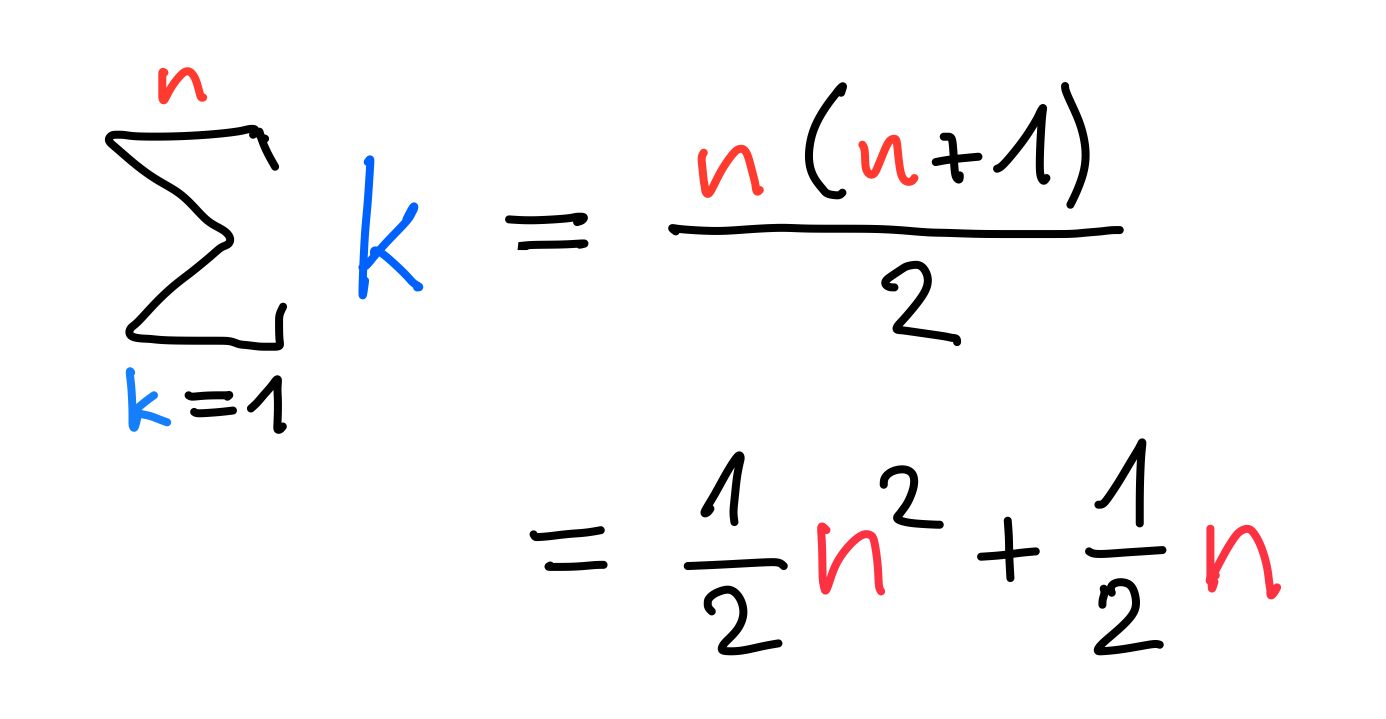
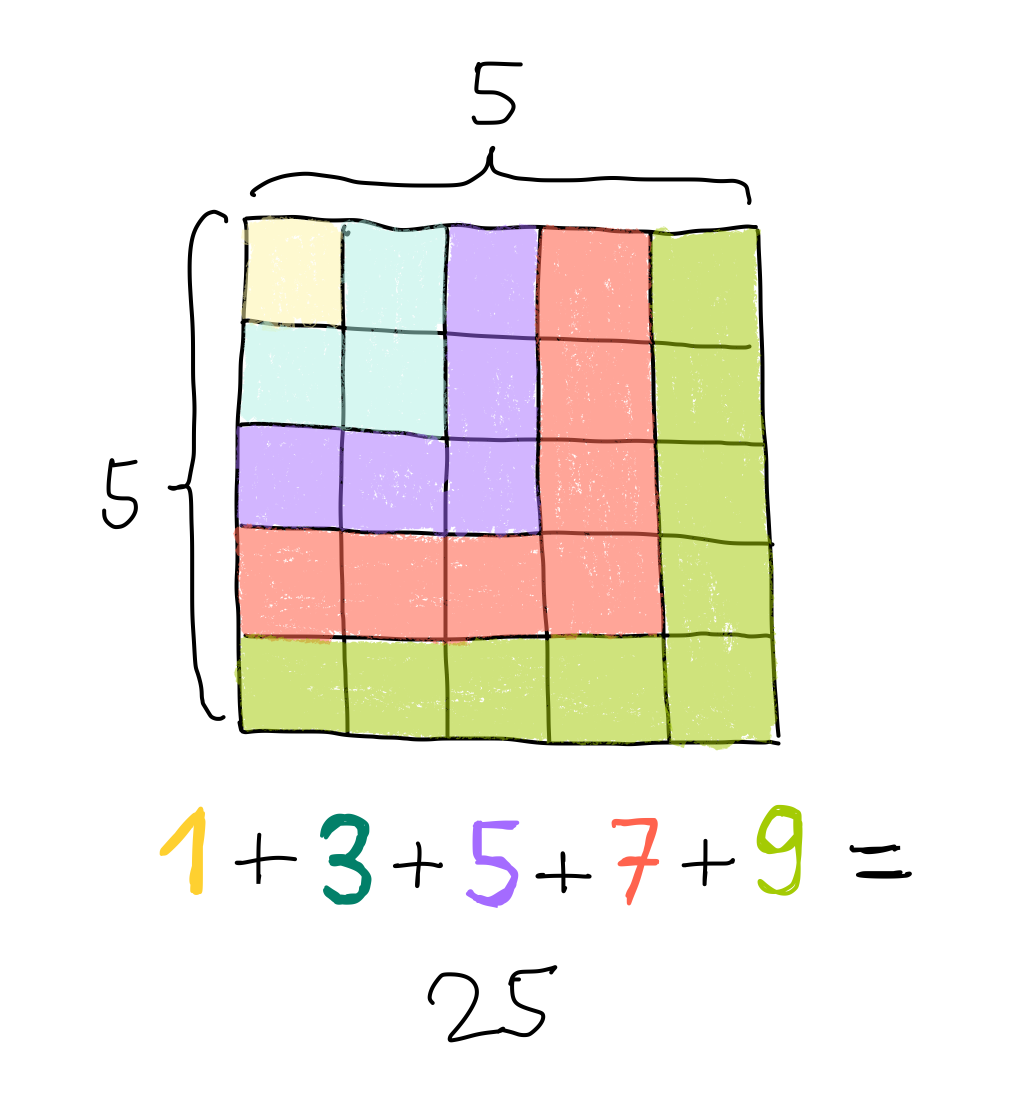
1+3+5+7+9+⋯+(2n-1)

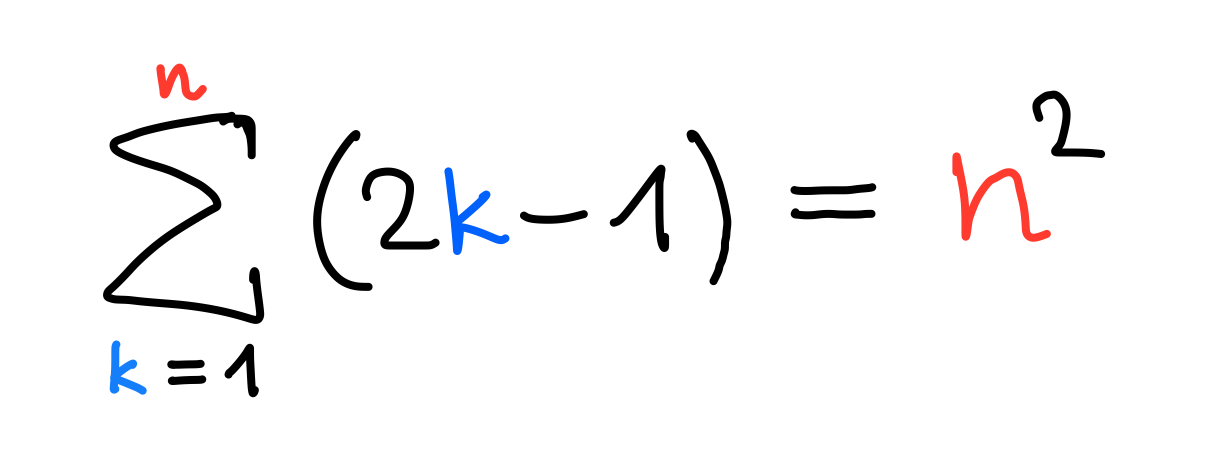
1²+2²+3²+4²+⋯+n²

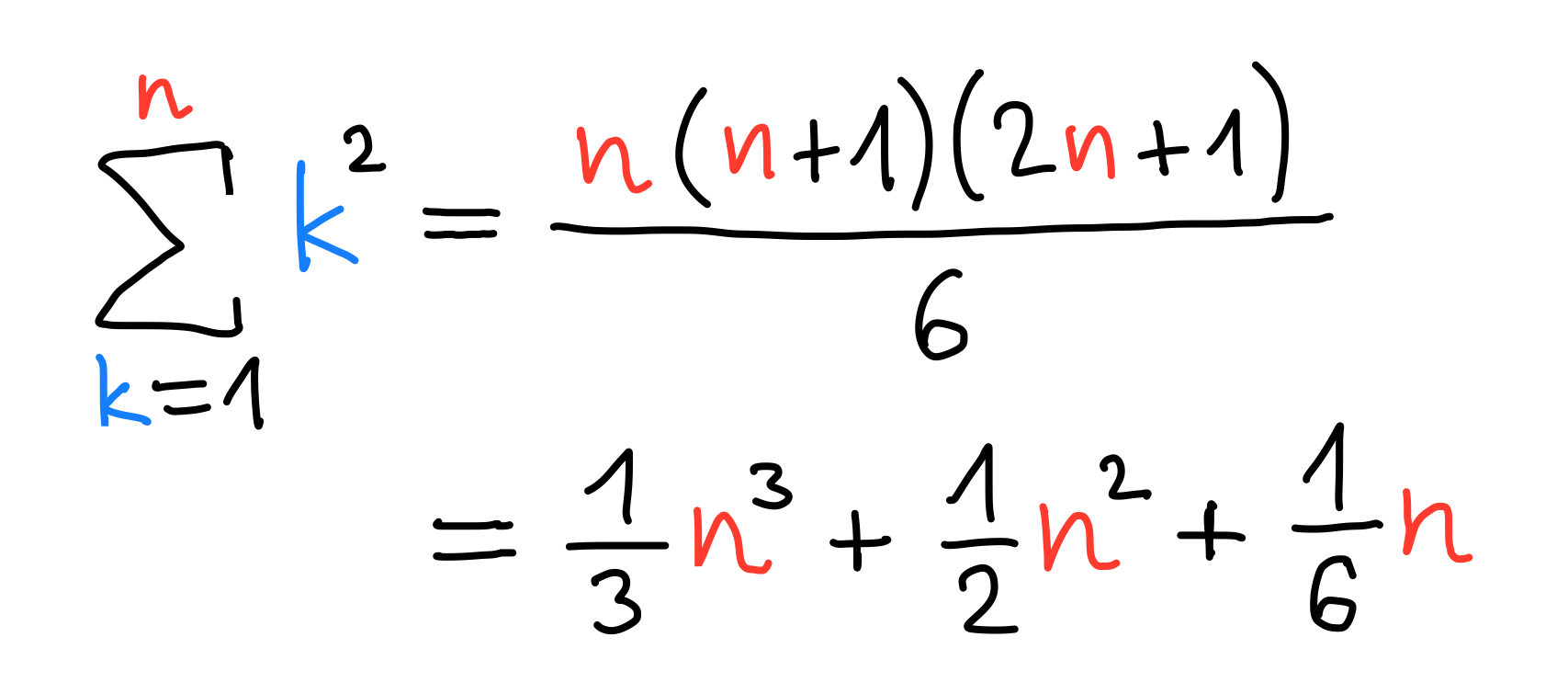
1³+2³+3³+4³+⋯+n³

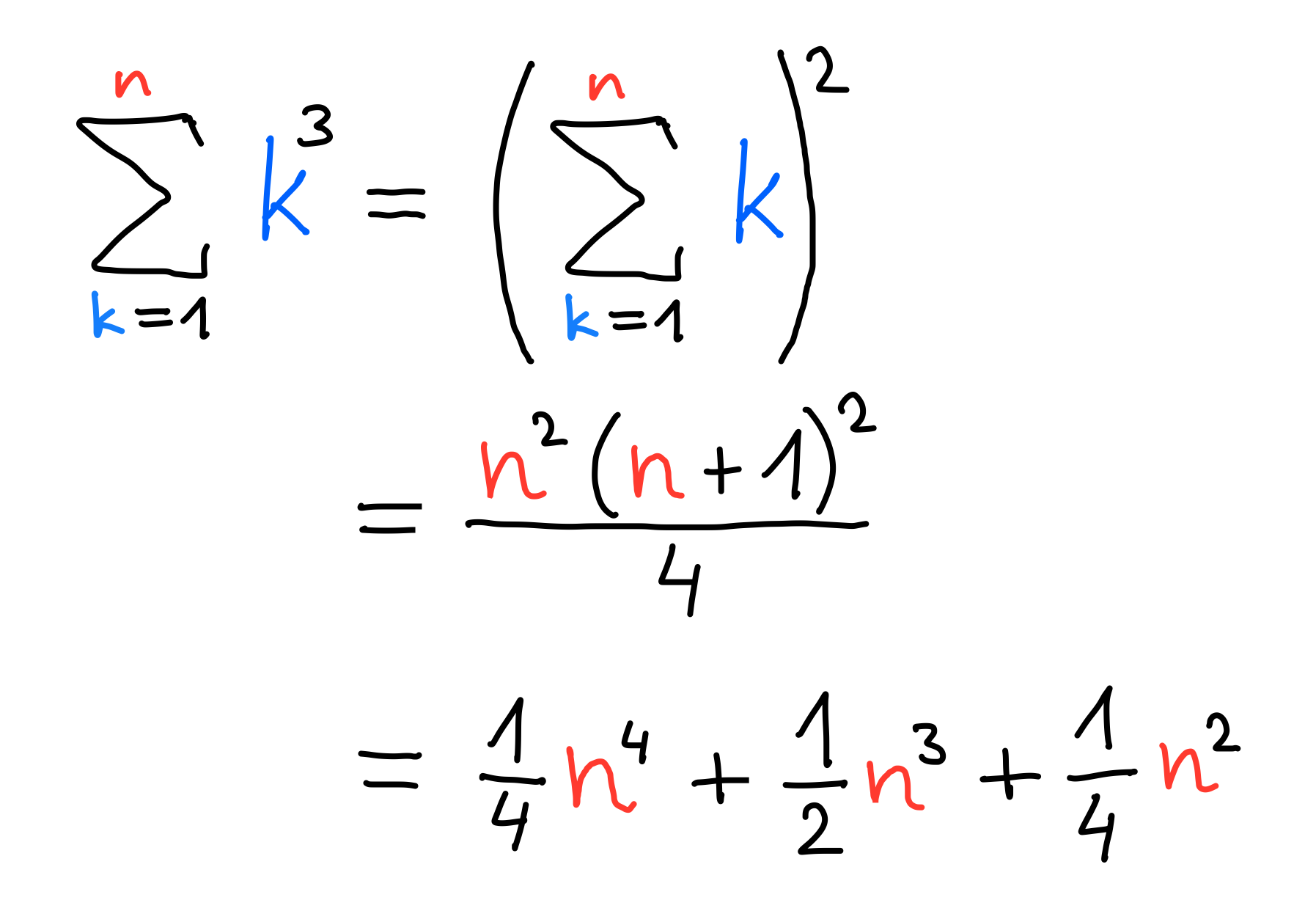
Pascal triangle

1

1

1

1

2

1

1

3

3

1

1

4

6

4

1

1

5

10

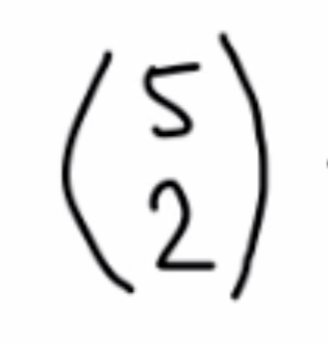
10

5

1

1

6

15

20

15

6

1

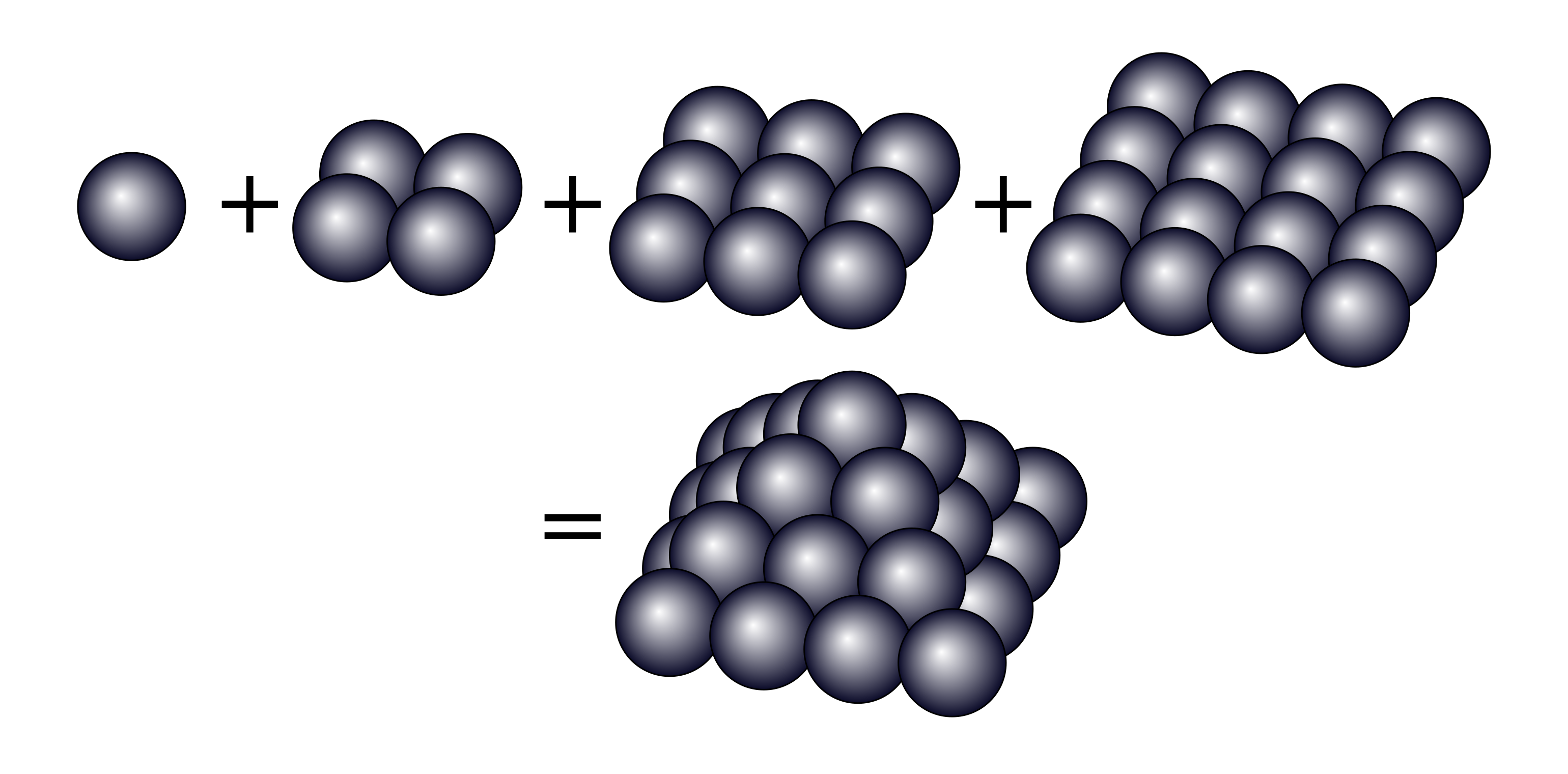
Picture proof

Picture proof

Pyramidal numbers

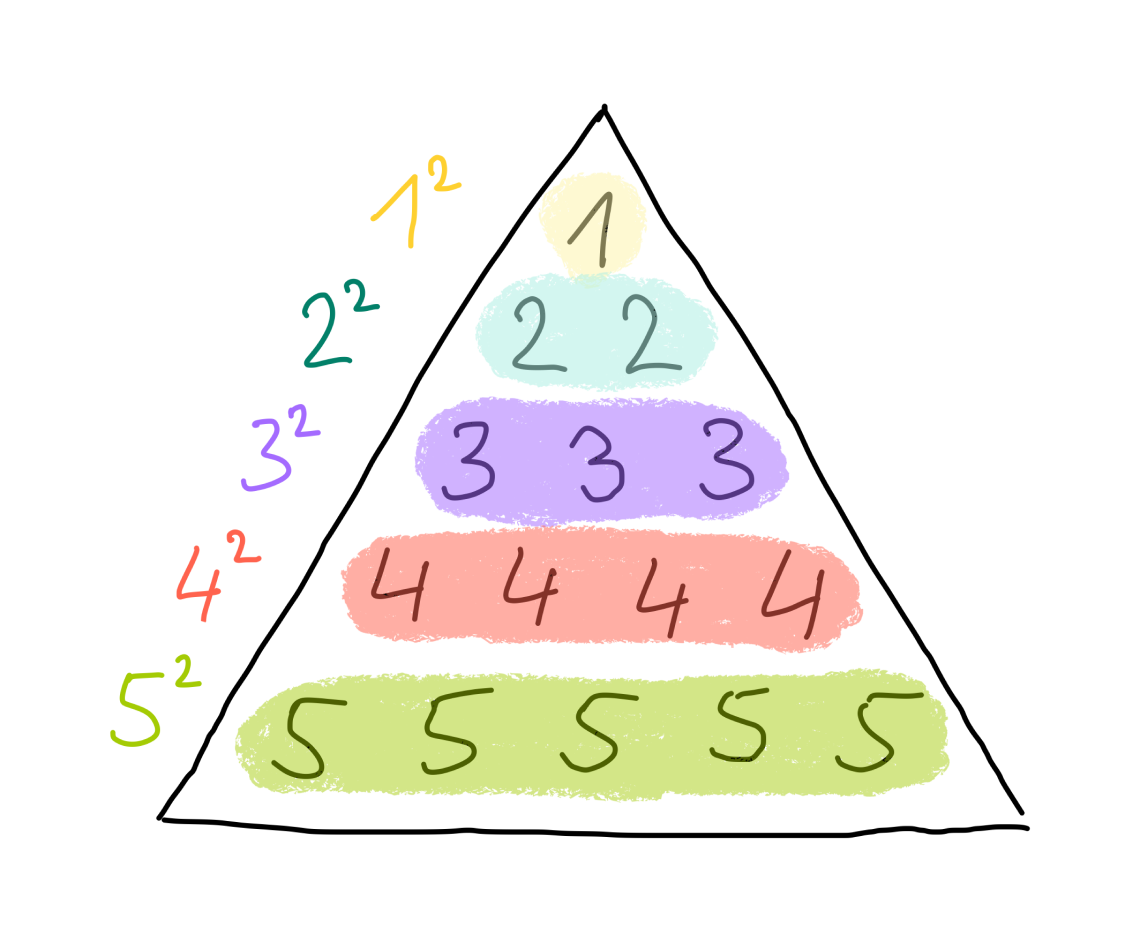
Place numbers into a triangle

Rotated 120 degrees

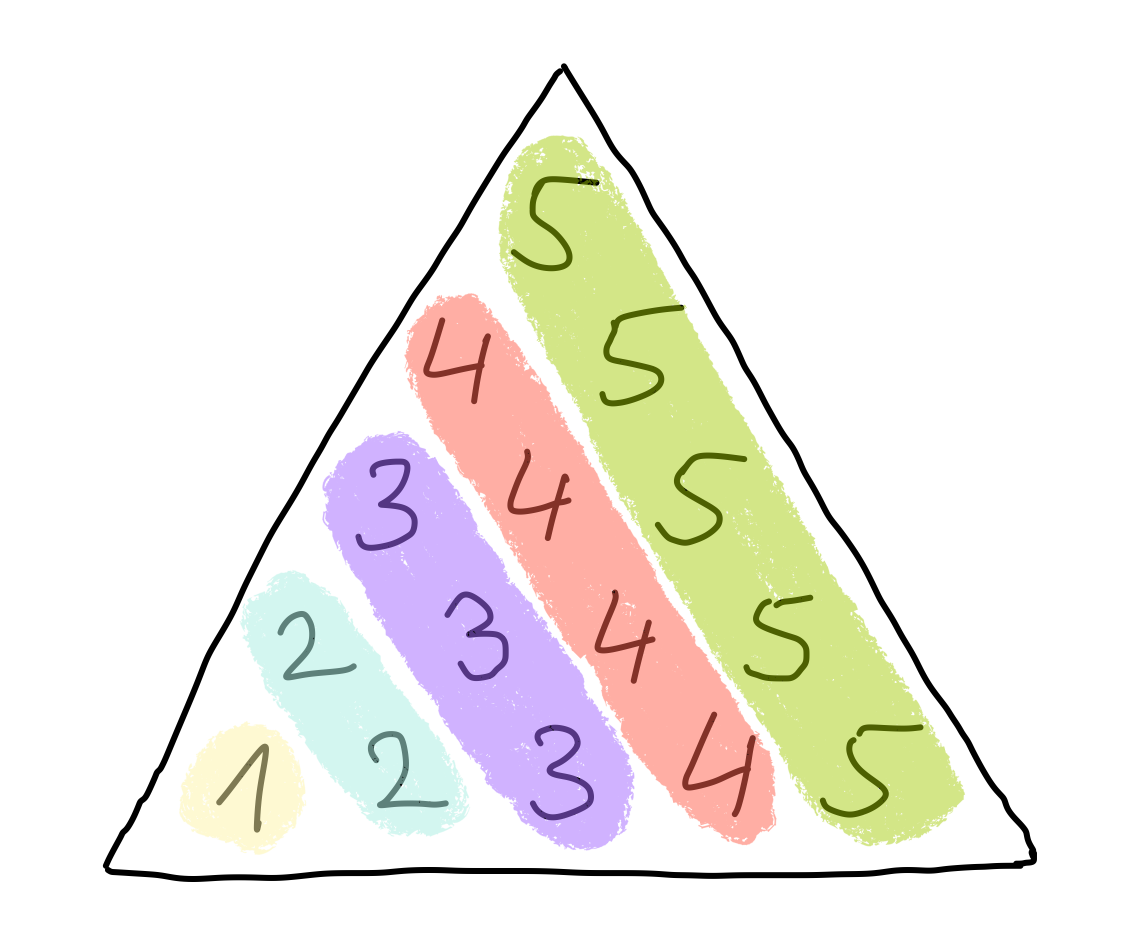
Rotated -120 degrees

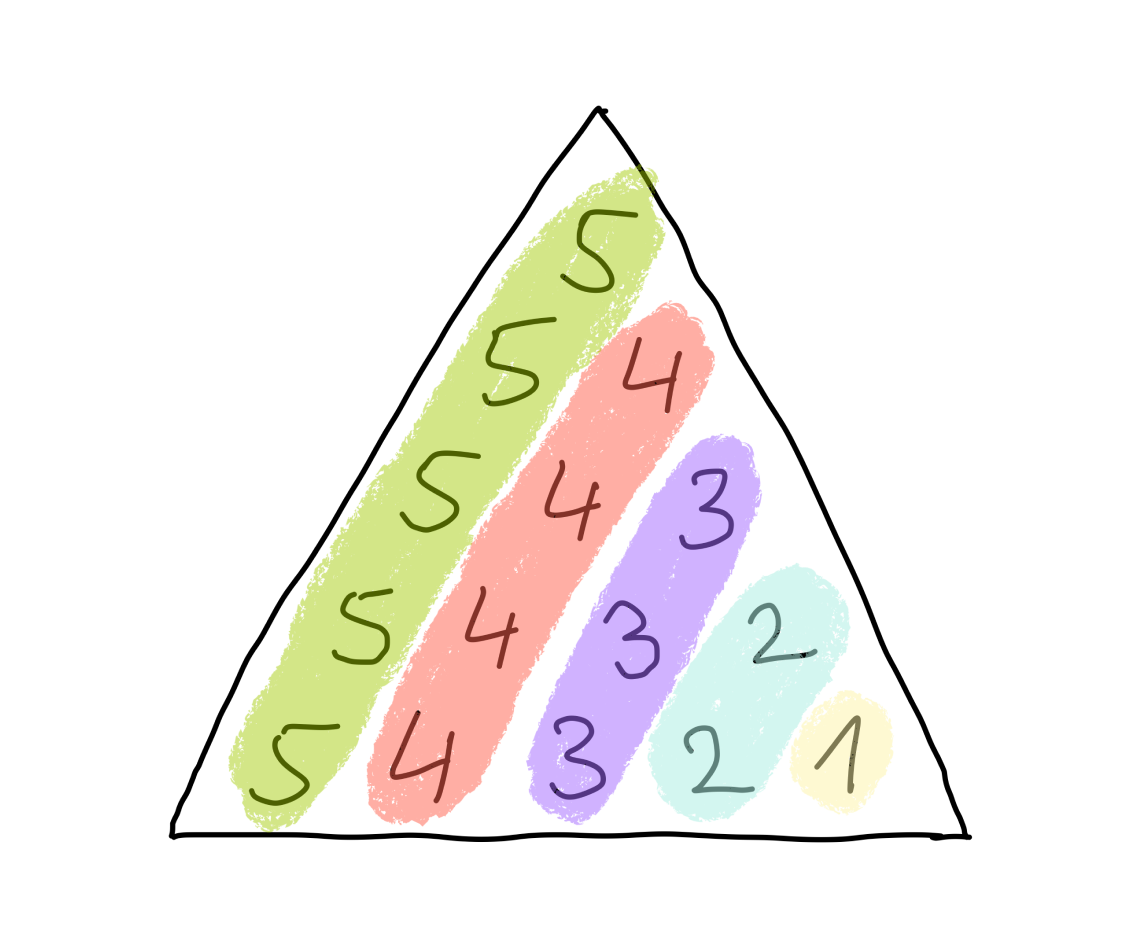
Adding all together

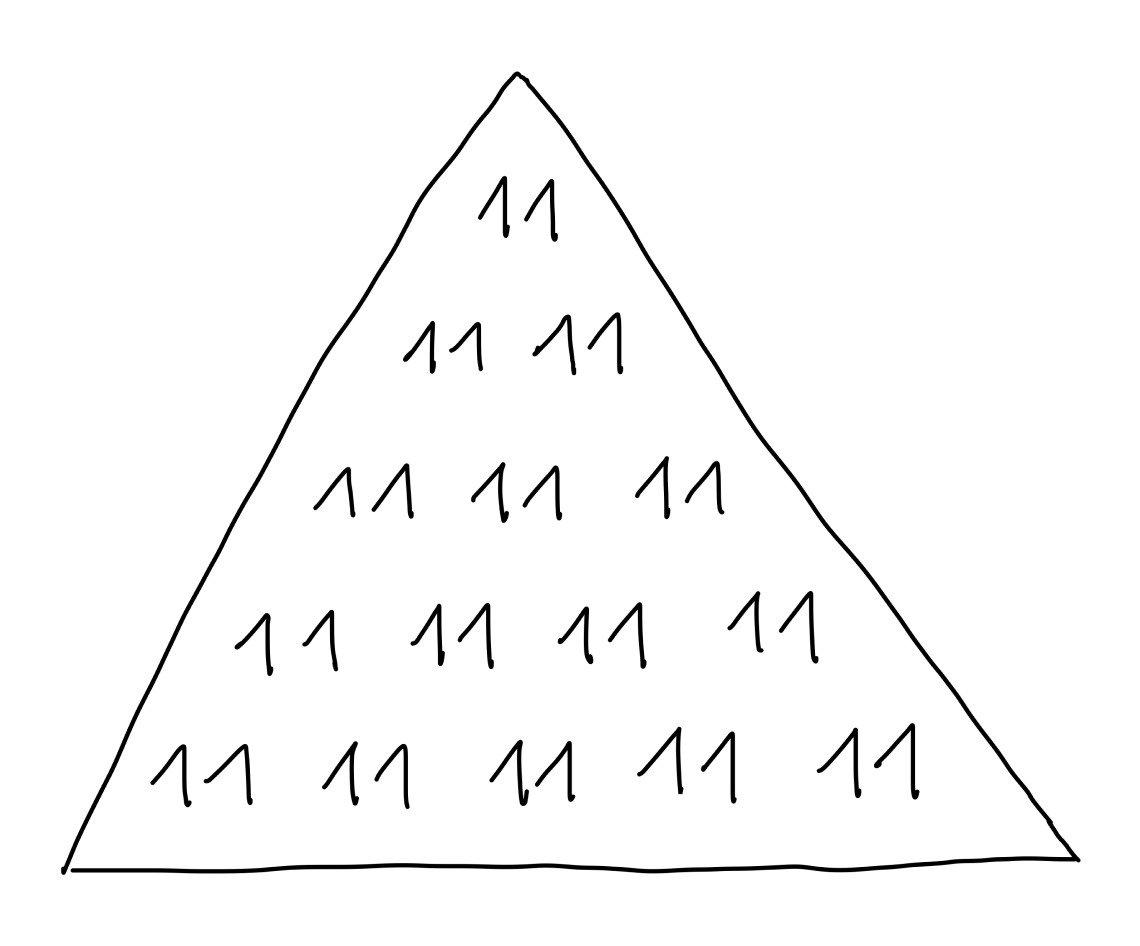
Picture proof

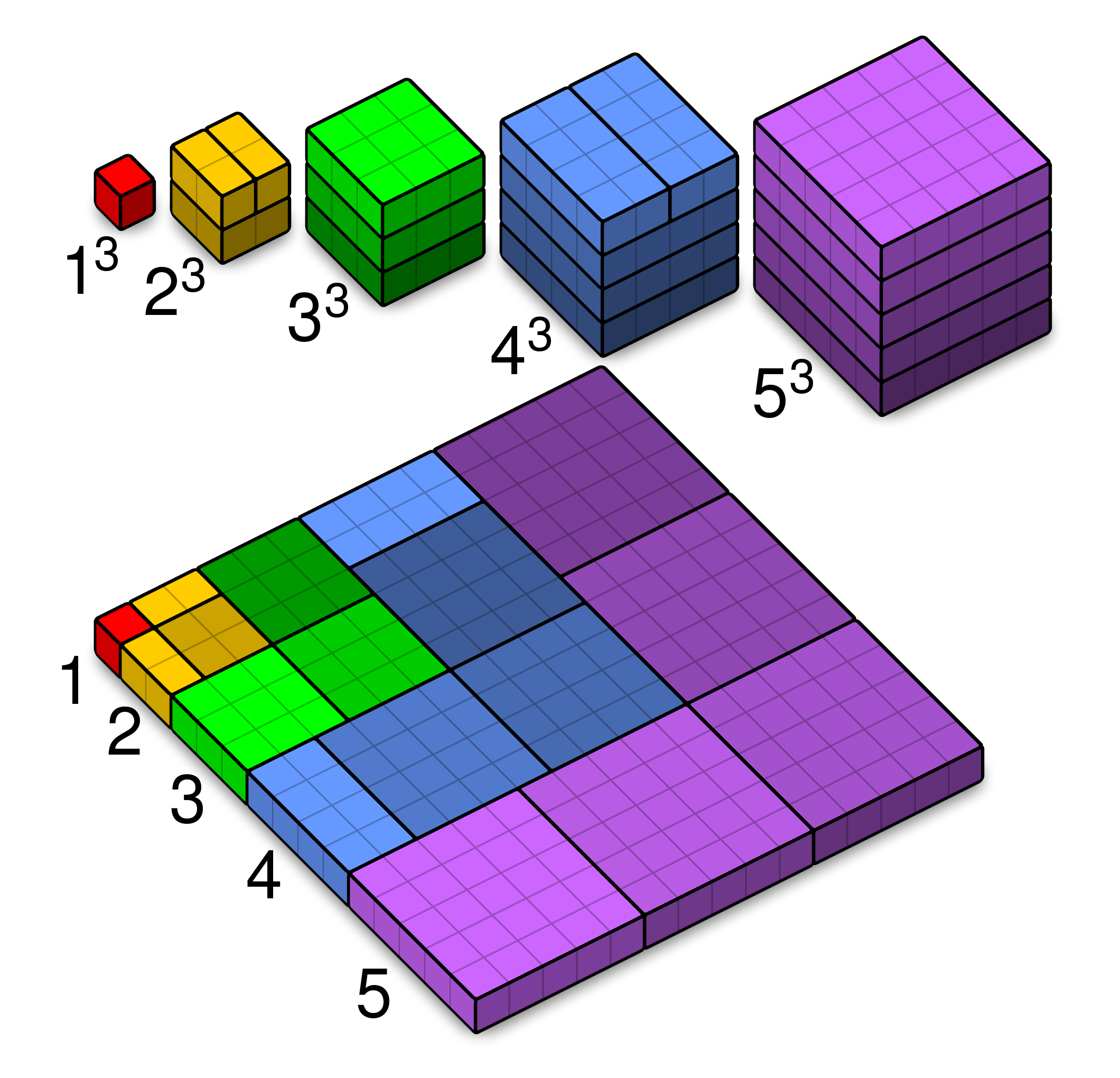
Summing multiplication table by columns

Summing multiplication table by L shapes

What is the pattern?

General statement

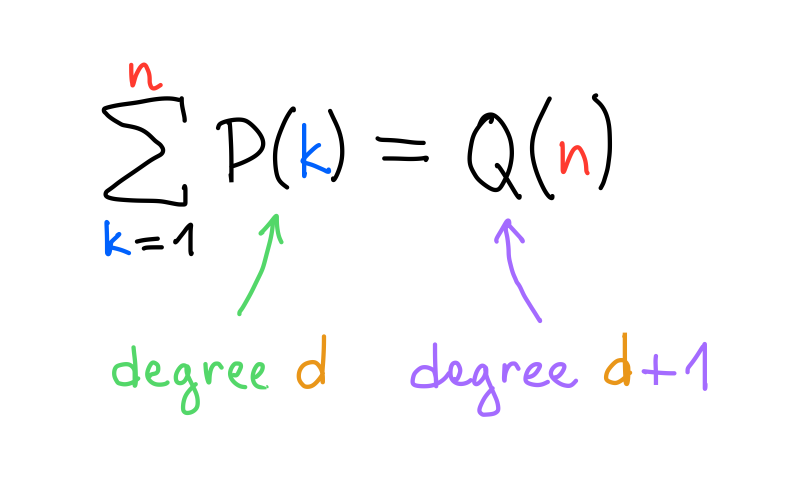
Computing coefficients of Q

System of linear equations

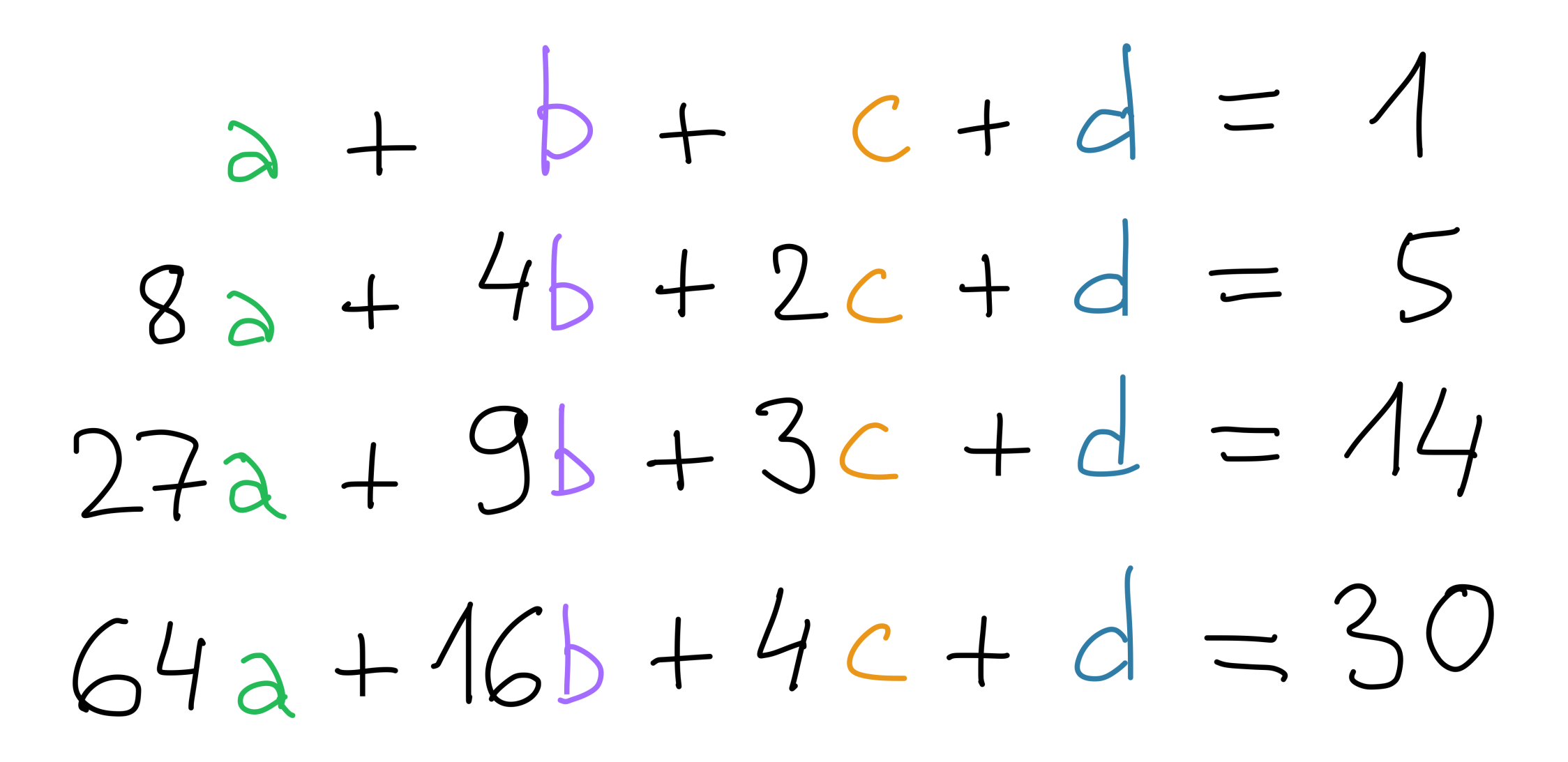
Gauss-Jordan elimination

1) Only needed for some polynomials P

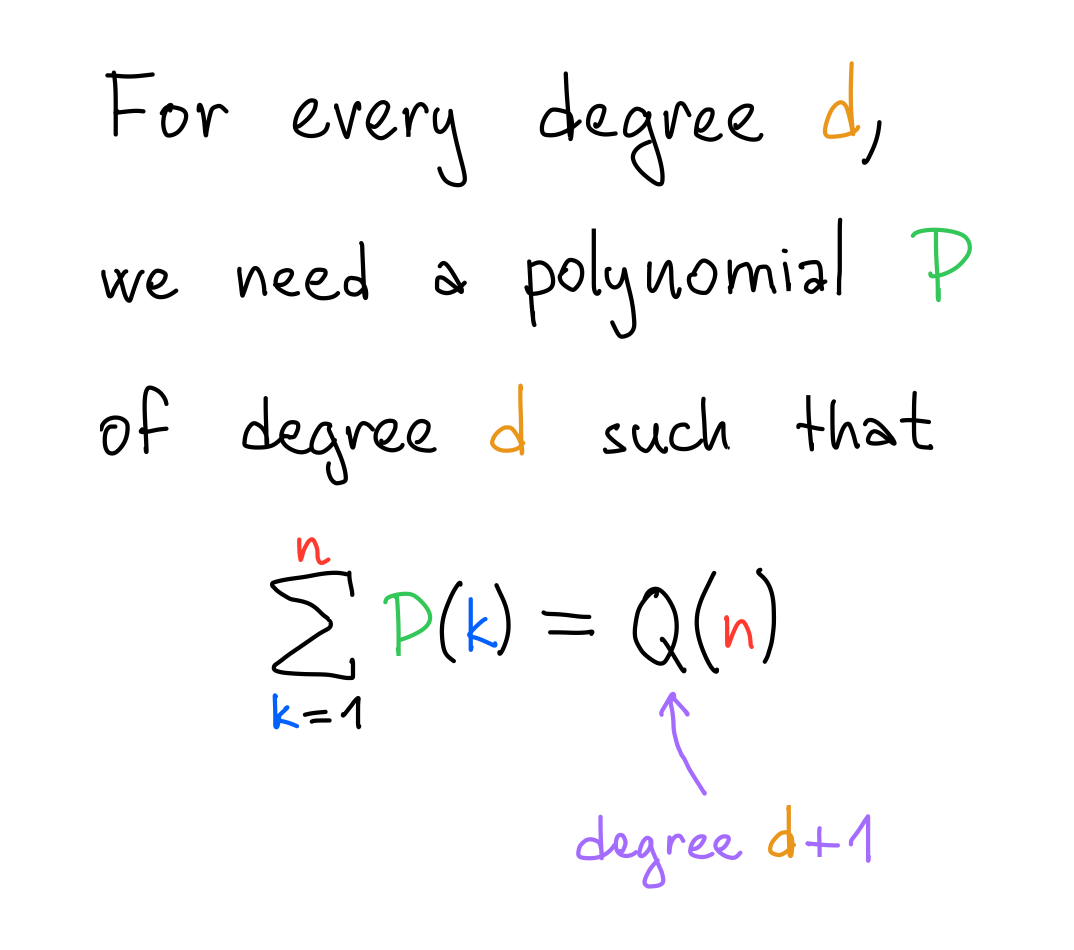
2) Prove it for these polynomials P

Linearity for adding

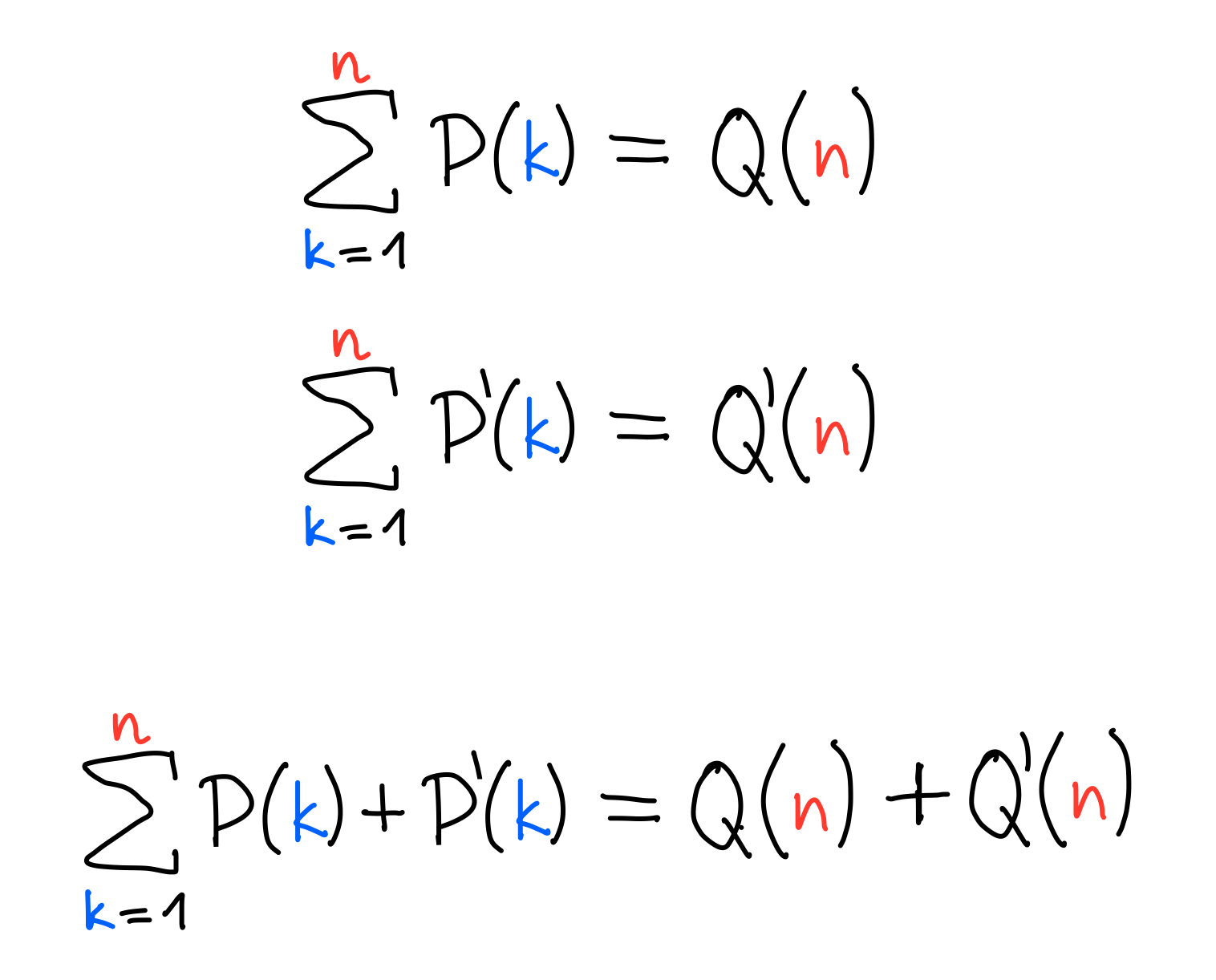
Linearity for multiplying

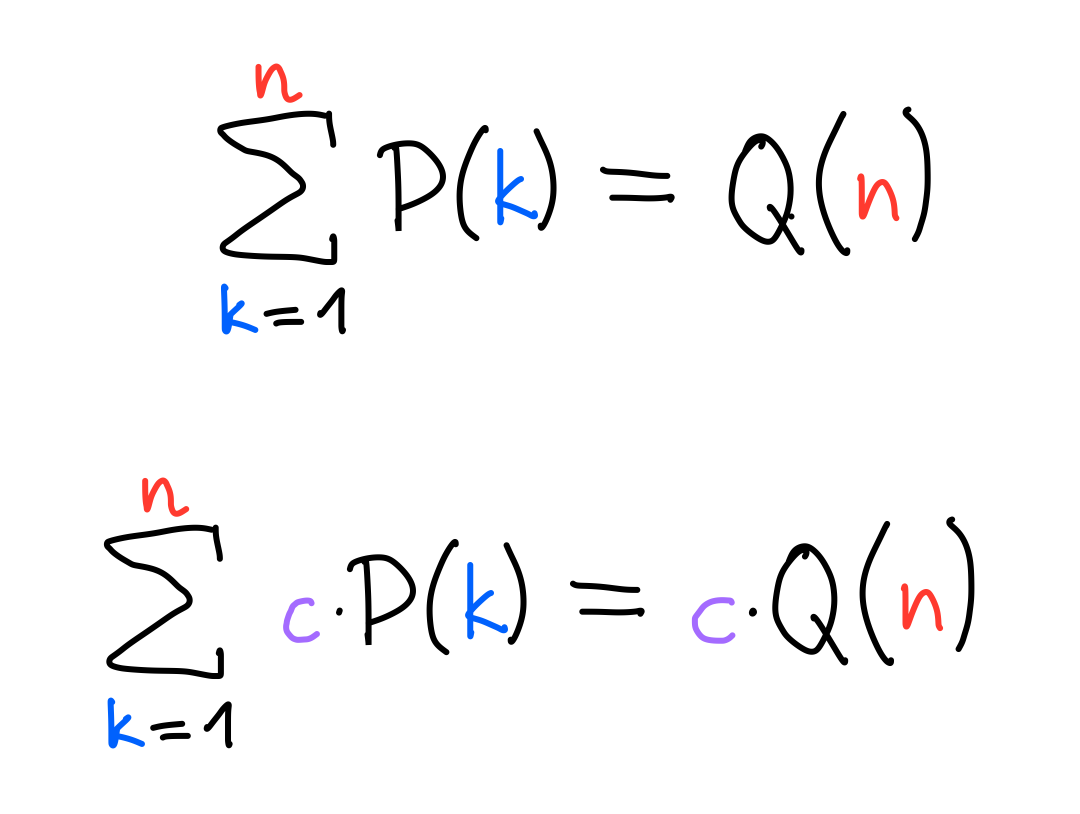
Combining sum of odd numbers

1+1+1+⋯+1=n

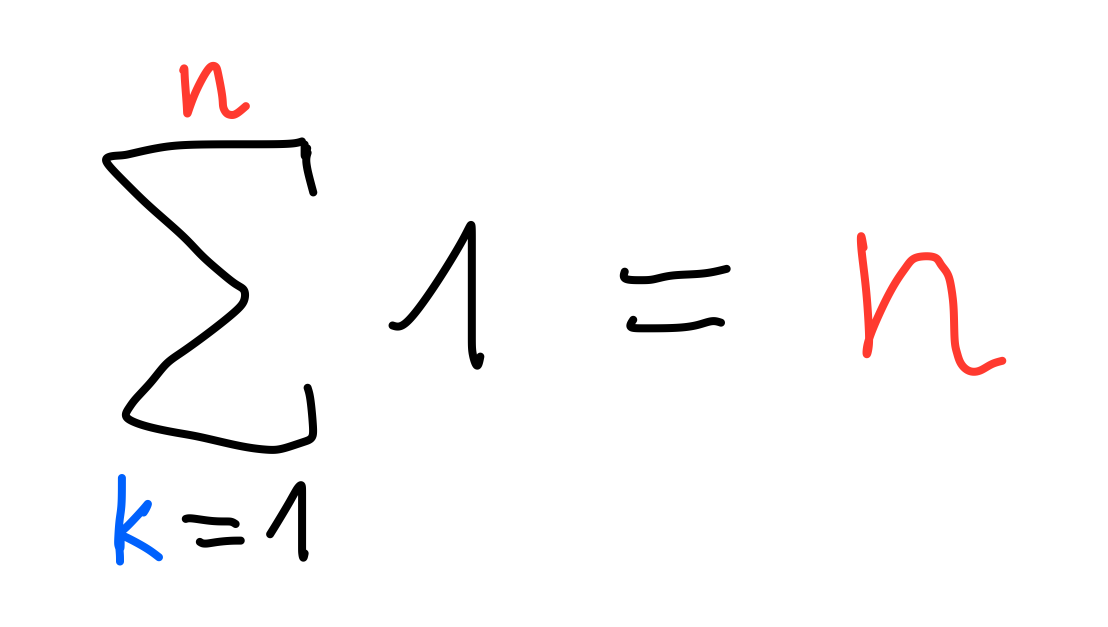
All degree 3 polynomials done

Sums of powers (Faulhaber's formula)

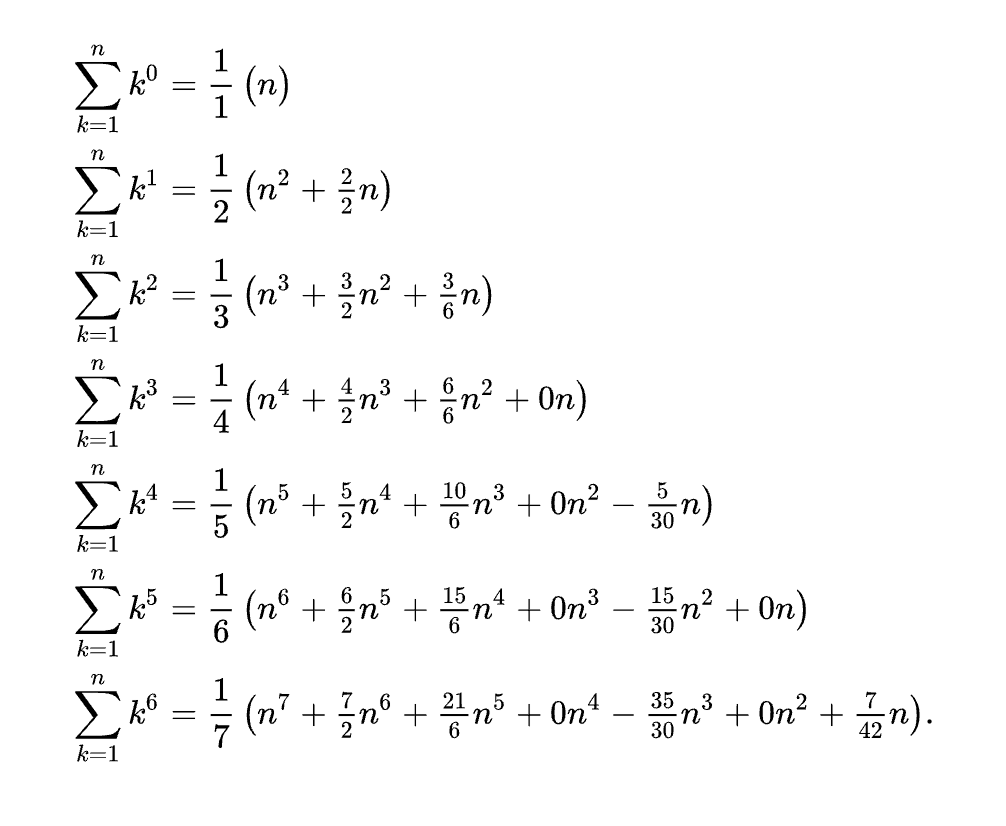
Standard proof using generating functions

Any degree 4 polynomial helps

Implies 1⁴+2⁴+3⁴+⋯+n⁴

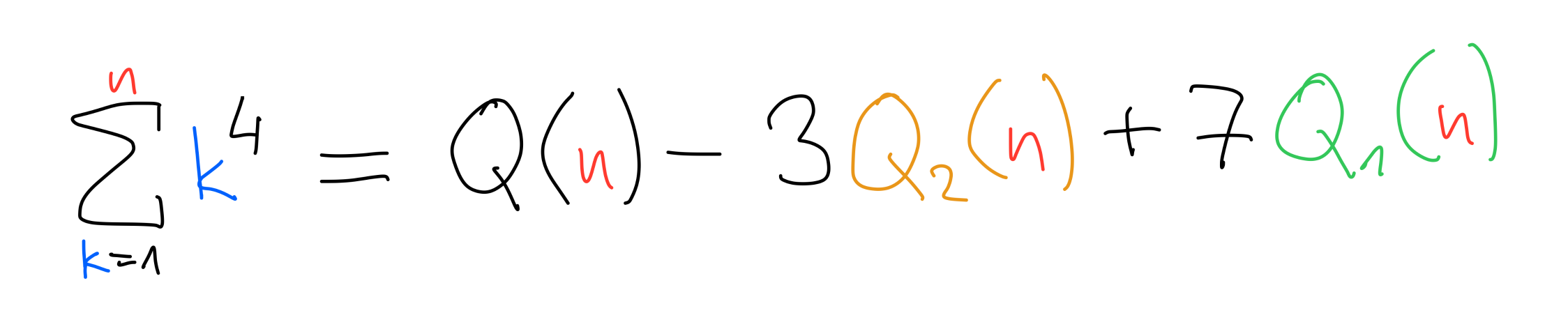
Number of paths

All 10 paths

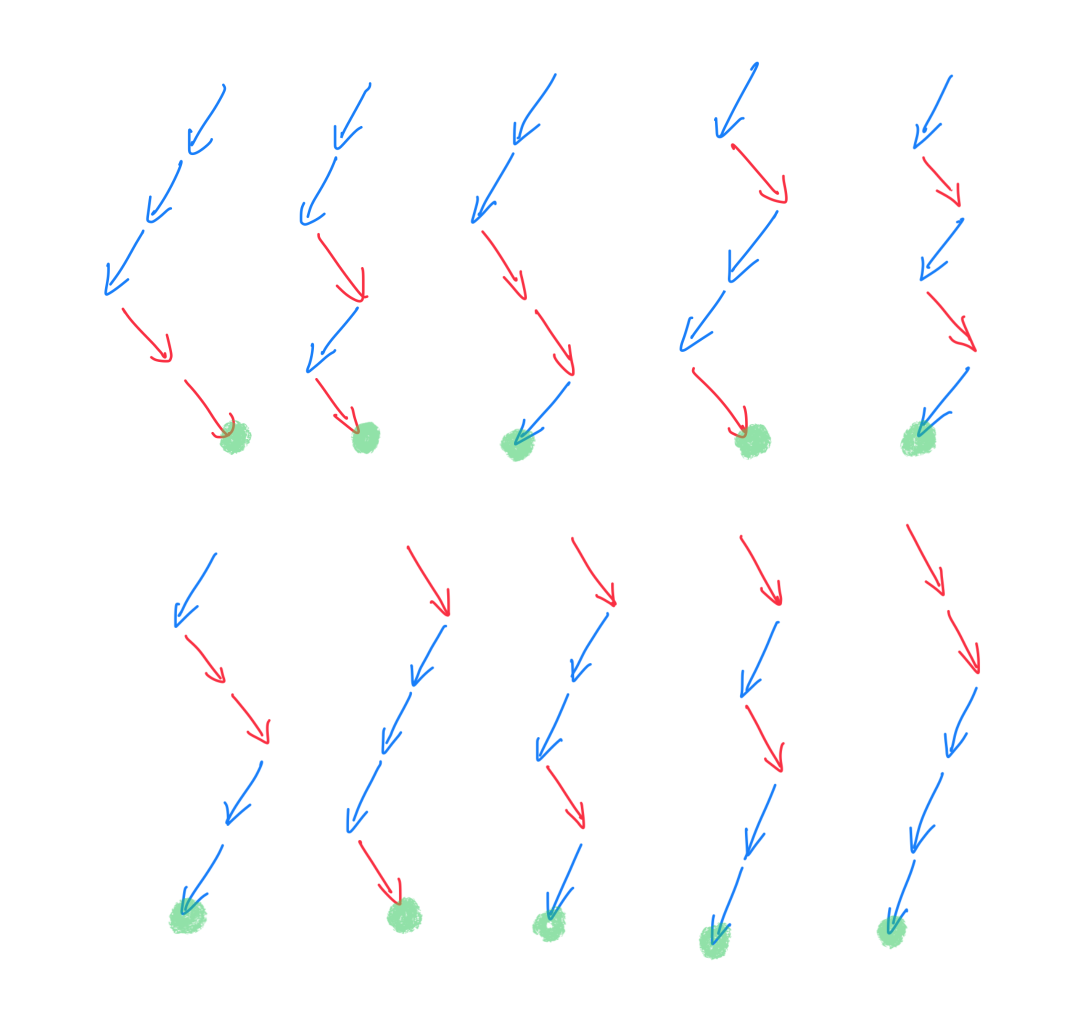
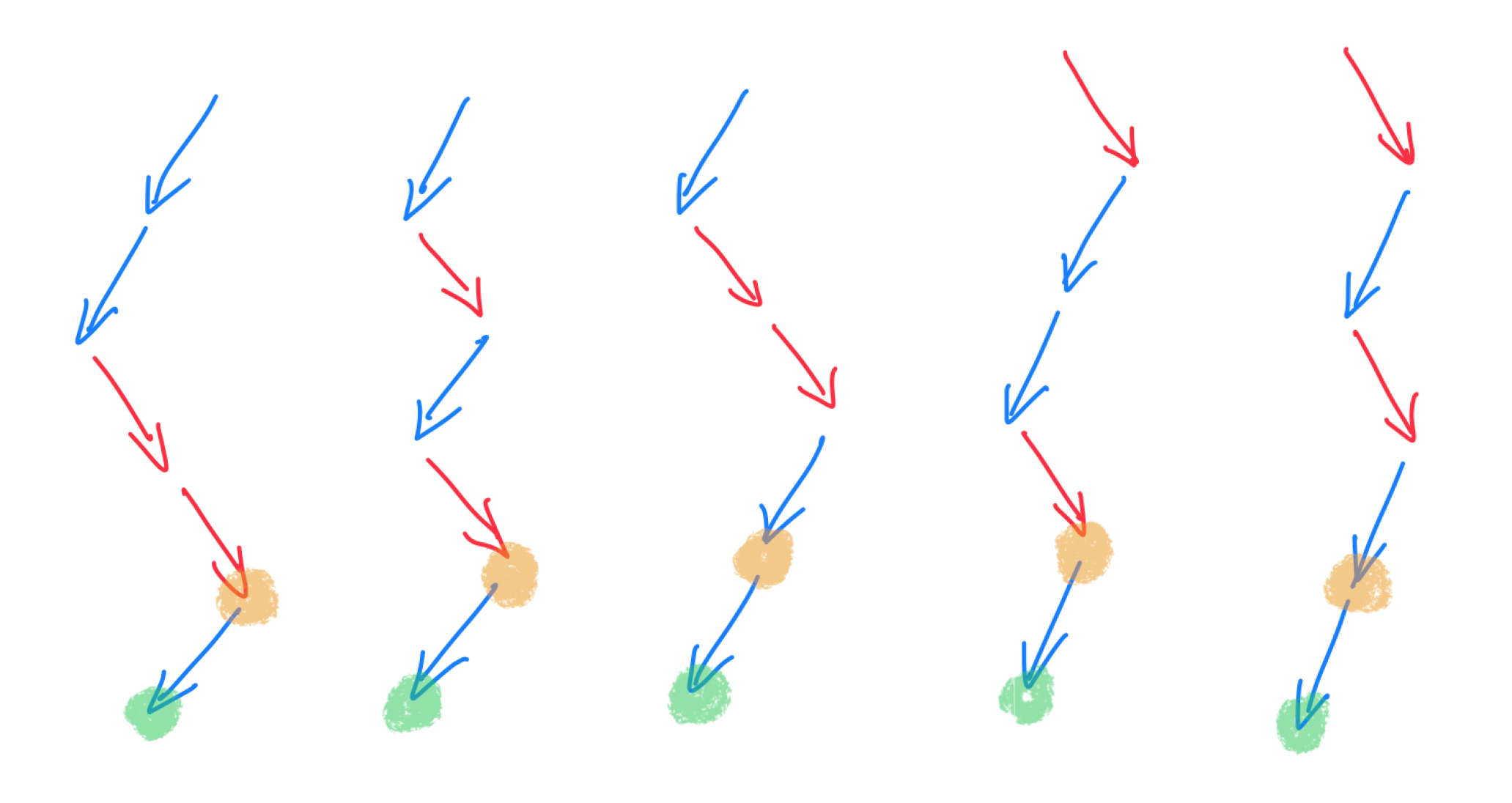
Addition of paths

Extended paths with a right step

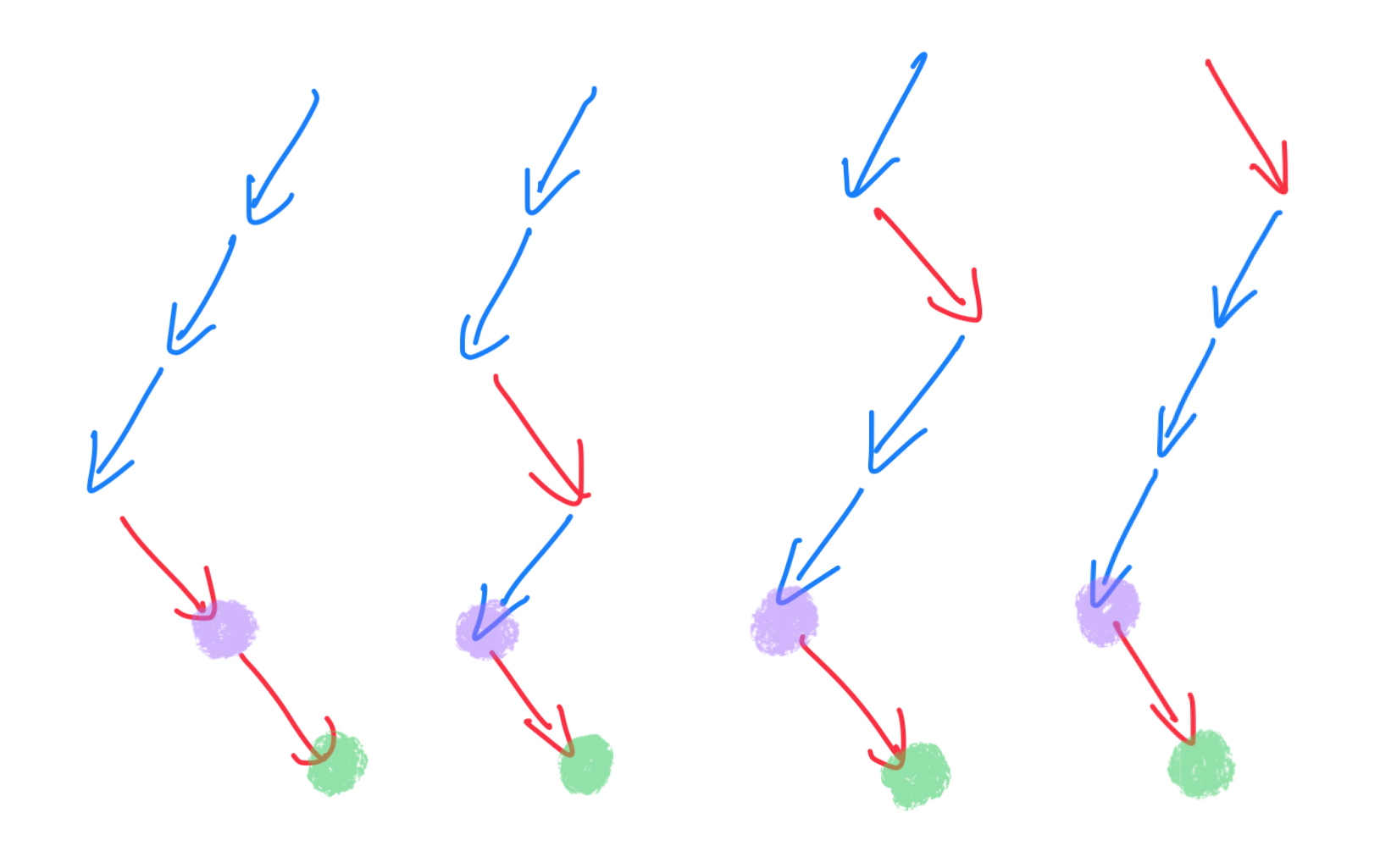
Extended paths with a left step

k=0

n=0

k=1

n=1

k=2

n=2

k=3

n=3

k=4

n=4

k=5

n=5

k=6

n=6

n choose k

Computing directly

General formula

Patterns within Pascal triangle

Vertical symmetry

Sum of a row

Sum of odd/even indexes in a row

Sum of squares of a row

Fibonacci numbers

Highlighting all odd numbers

Serpinski triangle

What about the hockey stick?

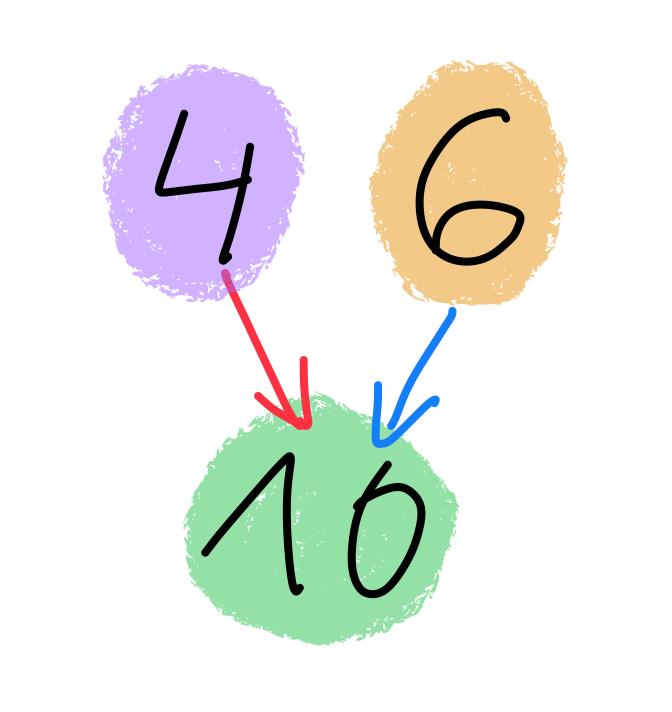
Hockey stick identity

Hockey stick identity for d=4

Deriving formula for 1⁴+2⁴+3⁴+⋯+n⁴

Previously known sums

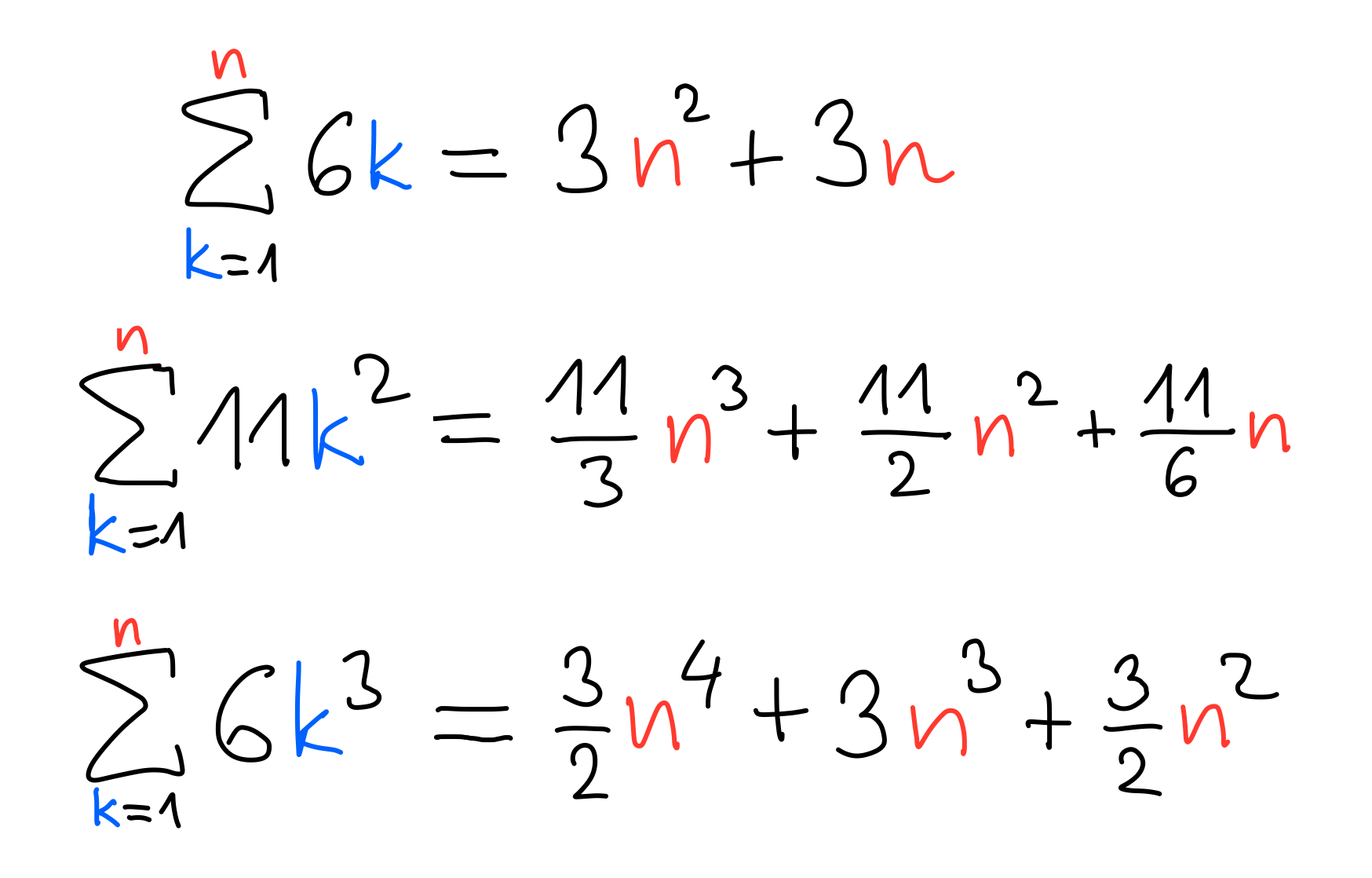
OrgPad

orgpad.com

20% off

POLYNOMIALS