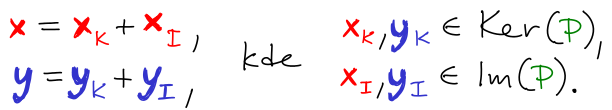Lineární algebra
Created by Pavel Klavík

Orgpage Lineární algebra
Autor: Pavel Klavík
Poslední změna: 24.11.2016
Poděkování: Zdeněk Hedrlín, Peter Zeman, studenti pokročilých cvičení.
Klíčová témata jsou v oknech se zvýrazněným pozadím. Ostatní okna mají barvu podle hlavního tématu, ke kterému patří. V současné chvíli jsou tato hlavní témata:
- Soustavy lineárních rovnic Ax=b.
- Matice.
- Vektorové prostory.
- Lineární zobrazení (homomorfismy).
Následující témata jsou rozpracovaná:
- Skalární součin, norma, ortogonalita.
- Determinanty.
- Vlastní čísla.
- Kvadratické formy a definitnost.
Asociace, kde je to nutné, jsou popsány v jednotlivých oknech (každé má dvě úrovně, jedna po najetí, druhá po kliknutí). Pro důležité asociace je vytvořeno speciální okno mezi pojmy, například pro maticovou reprezentaci lineárního zobrazení.
Zdroje
Obsah je utvořen podle výuky na
Pokročilých cvičeních z Lineární algebry a knih
Povídání o lineární algebře a
Lineární algebra II: Pokročilé cvičení (převzaty skoro všechny obrázky).
Grupy
Matematická struktura 𝔾 spolu s binární operací ∘ : 𝔾 ⨯ 𝔾 → 𝔾 se nazývá grupa, pokud splňuje následující vlastnosti:
- Platí asociativita: a∘(b∘c) = (a∘b)∘c.
- Existuje neutrální prvek e, že a∘e = e∘a = a.
- Existují inverzní prvky a-1, že a∘a-1 = a-1∘a = e.
Čísla typicky tvoří grupu, například ℤ je grupa pro sčítání. Struktura ℤn tvořená prvky {0,1,...,n-1}, s operací sčítání modulo n je grupa. Tyto grupy jsou však značně speciální, typická grupa je nekomutativní.
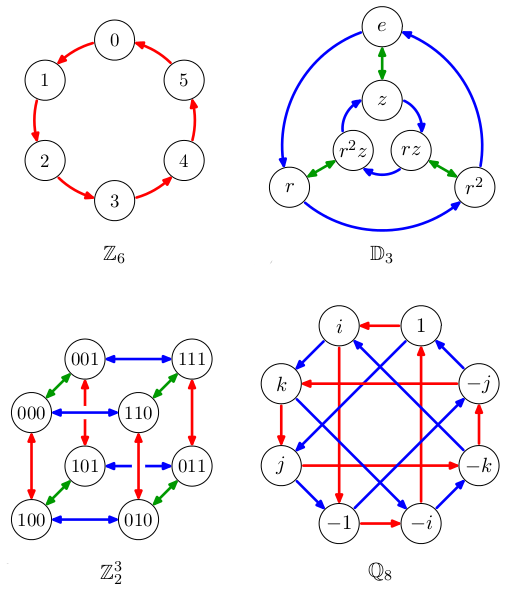 Cayley vymyslel v 1878 způsob, jak vizualizovat grupy pomocí diagramů. Vrcholy jsou jednotlivé prvky grupy 𝔾. Hrany popisují množinu generátorů g1, ..., gk, pro kterou
Cayley vymyslel v 1878 způsob, jak vizualizovat grupy pomocí diagramů. Vrcholy jsou jednotlivé prvky grupy 𝔾. Hrany popisují množinu generátorů g1, ..., gk, pro kterou
⟨g1, ..., gk⟩ = 𝔾.
Jednotlivým generátorům přiřadíme barvy a i-tou barvou
nakreslíme šipky z x do gi∘x. Tím je zachycena struktura celé grupy a je to mnohem přehlednější než popisovat binární operaci ∘ tabulkou.
Grupy vlevo jsou
komutativní: grupa sčítání modulo 6 a grupa binárních vektorů. Grupy vpravo však
komutativní nejsou, například pro 𝔻
3 je modrá šipka následovaná zelenou něco jiného než naopak. Grupa 𝔻
3 je grupa
symetrických transformací rovnostranného trojúhelníka, kde operace ∘ je skládání. Grupa ℚ
8 je grupa imaginárních jednotek kvaternionů (zobecnění komplexních čísel) a operace popisuje jejich násobení.
Lineární (ne)závislost
Vektor u je v množině X nadbytečný, pokud ⟨X \ {u}⟩ = ⟨X⟩. Nadbytečné vektory můžeme z množiny postupně odebírat a nezmění se její lineární obal. Motivace je, že chceme lineární obal ⟨X⟩ popsat pomocí co nejmenší množiny vektorů.
Uvažme rovinu vzniklou jako lineární obal tří vektorů. Libovolný z nich je nadbytečný, jeho odebráním se obal nezmění. Po odebrání nejsou již zbývající dva vektory nadbytečné.
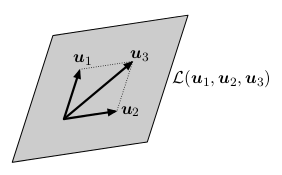
Povšimněme si, že počátek
0 je vždy nadbytečný.
Množina vektorů X je lineárně závislá, pokud obsahuje nadbytečný vektor, a lineárně nezávislá jinak.
Tvrzení: Následující definice lineární závislosti x1,...,xn jsou ekvivalentní:
- Obsahuje nadbytečný vektor.
- Existuje vektor xi, který je lineární kombinací zbývajících.
- Existuje netriviální lineární kombinace nuly:
0 = c1*x1 + ... + cn*xn, že alespoň jeden z koeficientů ci je nenulový.
- Existuje vektor v lineárním obalu, který lze vyjádřit jako dvě různé lineární kombinace.
Tagy: #klicove
Algebraická tělesa
I když jsme skoro celou lineární algebru popisovali nad reálnými čísly ℝ. Avšak celou řadu speciálních vlastností ℝ jsme nikdy nepoužili. Například pro řešení soustavy lineárních rovnic Gaussovou eliminací nepotřebujeme vědět, že existují odmocniny nebo limity Cauchyovských posloupností. Můžeme proto místo ℝ použít libovolnou matematickou strukturu čísel zvanou algebraické těleso, která splňuje několik pravidel.
Definice algebraického tělesa. Matematická struktura 𝕋 spolu s dvěma binárními operacemi sčítání + : 𝕋 ⨯ 𝕋 → 𝕋 a násobení * : 𝕋 ⨯ 𝕋 → 𝕋 se nazývá těleso, pokud splňuje následující vlastnosti:
- 𝕋 je vzhledem k operaci sčítání grupa a označme 0 její neutrální prvek.
- 𝕋 ∖ {0} je grupa vzhledem k operaci násobení, jejíž neutrální prvek označme 1.
- Platí distributivita: a*(b+c) = a*b+a*c.
Tedy těleso jsou dvě grupy svázané distributivitou.
Příklady těles. Vyjma ℝ jsou standardní příklady nekonečných těles komplexní čísla ℂ a racionální čísla ℚ. Existují i konečná tělesa, která jsou dokonce přesně charakterizovaná.
Zobecnění vektorových prostorů. Ve většině diagramu se uvažují vektorové prostory nad tělesem reálných čísel ℝ, tedy prostory ℝn. Je však možné uvažovat prostory nad libovolným tělesem 𝕋. V konkrétní definici dostáváme prostory 𝕋n, v abstraktní defici jsou skaláry z 𝕋 místo ℝ. Také matice se uvažují nad tělesem 𝕋 jako 𝕋m x n. Například v informatice je užitečný prostor binárních vektorů ℤ2n.
Velká část výsledků lineární algebry popisovaných v tomto diagramu funguje bez jakékoliv změny pro vektorové prostory nad obecnými tělesy 𝕋. V následujících částech jsou odlišnosti:
- Nemusí platit nezávislost fundamentálních podprostorů, jediný možný důkaz musí využívat ortogonalitu. Například matice A = (1,1) nad ℤ2 má R(A) = Ker(A).
- Standardní skalární součin lze uvažovat, ale nemusí splňovat pozitivní definitnost.
- Norma proto nedává smysl a ortogonalita se chová velice odlišně: nenulový vektor může být kolmý sám k sobě, například (1,1) nad ℤ2.
- Vlastní čísla nemusí existovat, protože polynom nad jiným tělesem než ℂ nemusí mít kořeny.
- Definitnost matic nedává smysl, protože nad tělesem nemusí existovat uspořádání.
Steinitzova věta o výměně
Věta: Nechť X je libovolná množina vektorů a Y je lineárně nezávislá množina vektorů z ⟨X⟩. Potom existuje Z ⊆ X, že |Z|=|Y| taková, že
⟨X \ Z ∪ Y⟩ = ⟨X⟩.
Tato věta má řadu zajímavých důsledků:
- Vektorový prostor obsahuje spoustu bází a na jejich vektorech není nic speciálního.
- Libovolnou lineárně nezávislou množinu lze rozšířit na bázi.
- Vždy platí, že |X| ≥ |Y|. Proto každá lineárně nezávislá množina má velikost menší či rovnou libovolnému generátoru, a všechny báze jsou stejně velké.
Důkaz:
Nechť Y = {y1,...,yn}. Postupně vkládáme vektory Y jeden za druhým do X za pomocí lemmatu o výměně. Problém by však mohl být, že při vložení yi by lemma mohlo vyjmout předtím vložené yj.
Uvědomme si však, že v lemmatu o výměně můžeme zvolit jako z libovolné xk takové, že koeficient 𝛼k ≠ 0. Proto vždy při vkládání yi vyjmeme některý z vektorů X. Pokud by to nebylo možné, dostáváme, že yi je lineární kombinace ostatních vektorů z Y, což je spor s lineární nezávislostí Y.
Tagy: #klicove
Konečná tělesa
Konečné těleso je tvořeno konečně mnoha prvky a nazývá se Galoisovo těleso, značeno GF(n) pro n prvků. S konečnými tělesy se dobře pracuje v počítačích a mají třeba řadu aplikací v kryptografii a teorii kódování.
Nejjednodušší příklady těles jsou prvočíselné velikosti:
Tvrzení:
Struktura ℤn je tvořena prvky {0,1,...,n-1}, s operacemi sčítání a násobení definovanými modulo n. Struktura ℤn je těleso, právě když n je prvočíslo p.
Důkaz:
Pokud n není prvočíslo, je snadné ukázat, že neexistují inverzní prvky pro násobení. Existují 1 < a,b < n takové, že a*b = n. Tedy a*b = 0 v ℤn, což není v tělese možné.
Obtížnější je dokázat, že existují inverzní prvky pro násobení v ℤp. Stačí ukázat, že násobení k je bijekce na ℤp.
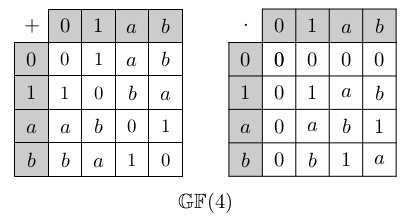 Složitější konečná tělesa však existují i pro jiné velikosti, například GF(4) vpravo.
Složitější konečná tělesa však existují i pro jiné velikosti, například GF(4) vpravo.
Věta: Každé konečné těleso je řádu pk, kde p je nějaké prvočíslo a k je přirozené číslo. Navíc pro každé pk těleso vždy existuje a je určené jednoznačně až na izomorfismus, tedy značení GF(pk) dává smysl.
Náznak důkazu: Mějme konečné těleso 𝕋, chceme dokázat, že jeho velikost je pk. Charakteristika 𝕋 je nejmenší počet jedniček, který se sečte na nulu, a vždy je to prvočíslo p. Tyto součty jedniček tvoří podtěleso izomorfní ℤp. Hlavní trik je, že 𝕋 tvoří vektorový prostor nad tělesem ℤp. Ten má nějakou dimenzi k, a proto obsahuje pk prvků.
Jednoznačnost tělesa velikosti pk vyplývá z věty o izomorfismu. Konstrukce takového tělesa je složitější a postupuje se přes okruhy polynomů a jejich rozkladová tělesa, detaily vynecháme.
Dimenze
Dimenze vektorového prostoru či jeho podprostoru je velikost libovolné jeho báze. Pro vektorový prostor V se dimenze značí dim(V).
To, že je dimenze dobře definována, vyplývá ze Steinitzovy věty o výměně. Mějme dvě libovolné báze X a Y. Můžeme vektory báze X vyměnit za vektory báze Y a naopak, proto musí mít stejně prvků.
Pozorování: Pokud U je podprostor V, potom dim(U) ≤ dim(V).
Tagy: #klicove
Konstrukce báze
Celá teorie bází by byla nezajímavá, pokud by žádná báze neexistovala. Dokážeme si s následujícím předpokladem, že báze vždycky existuje (a dokonce je spousta způsobů, jak je zvolit).
Předpoklad: Vektorový prostor má konečnou dimenzi, tedy libovolná báze má konečnou velikost. (Dokonce podle Steinitzovy věty by stačilo, že existuje báze konečné velikosti.)
Bez předpokladu bychom museli uvažovat i nekonečně dimenzionální vektorové prostory (třeba prostory funkcí nebo posloupností), pro než jsou potřeba nekonečné báze. Myšlenkově to funguje totožně, ale je s tím řada technických problémů, například musíme uvažovat nekonečné lineární kombinace.
Nefungující nápad: odebírání z generátoru. Začneme s libovolným generátorem vektorového prostoru (například celým vektorovým prostorem U) a budeme z něj postupně odebírat nadbytečné vektory. Skončíme s lineárně nezávislým generátorem, neboli bází.
Problém je, že typicky bude generátor nekonečný i v konečně dimenzionálním vektorovém prostoru. Odebíráme nekonečně mnoho vektorů, navíc můžeme skončit s prázdnou množinou (problém nekonečna). Například v ℝ postupně odebereme všechny vektory přímky, protože každý bude nadbytečný vůči zbývajícím.
Fungující nápad: přidávání vektorů. Půjdeme na to proto obráceně, začneme s prázdnou množinou a budeme do ní postupně přidávat vektory při zachování lineární nezávislosti.
Nechť Y0 = ∅ a Yk je zkonstruovaná nezávislá množina s k vektory. Skončíme, pokud ⟨Yk⟩ je celý prostor U. Jinak zvolíme libovolný vektor yk+1 ∊ U ∖ ⟨Yk⟩ a pokračujeme dál. Postup skončí po konečně mnoha krocích kvůli předpokladu a zkonstruuje bázi U.
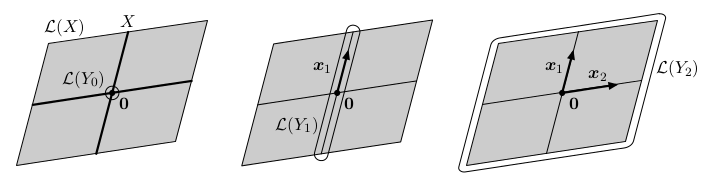
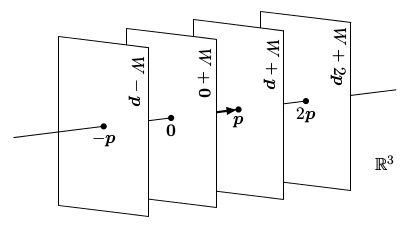
Afinní podprostory
Afinní podprostory jsou zobecněním vektorových podprostorů. Afinní podprostor W+p vznikne z vektorového podprostoru W posunutím z počátku o vektor p:
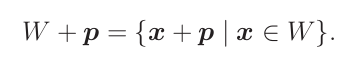
Navíc uvažujeme i prázdnou množinu jako afinní podprostor. Například afinní podprostory ℝ3 jsou prázdná množina, všechny body, všechny přímky, všechny roviny a celý prostor.
Tvrzení: Platí, že W+p = W+q, právě když p-q ∊ W.
Důkaz:
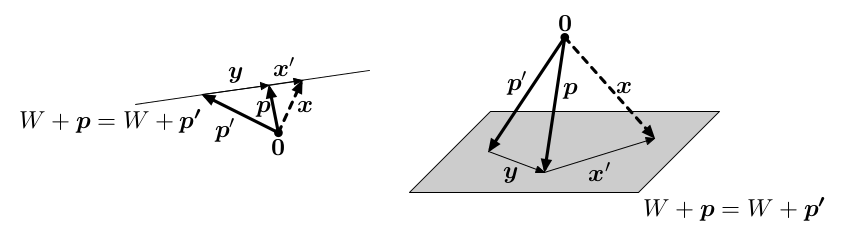
Navíc W+
0 = W, tedy W+
p = W, právě když
p ∊ W.
Afinní podprostory jsou
velice zajímavé strukturálně, více informací u faktorprostorů.
Tagy: #klicove
Vlastnosti vektorů ℝ n
Pokud pracujeme s abstraktní definicí vektorového prostoru, máme zaručeno několik vlastností vektorů: sčítání vektorů je komutativní, asociativní, platí distributivity s násobením, existuje nulový vektor, atd.
Pokud použijeme konstruktivní definici ℝn, můžeme snadno dokázat, že vektory také splňují všechny tyto vlastnosti. Například nulový vektor je počátek 0 = (0,...,0).
Ukažme si myšlenku alespoň na jednom příkladu.
Tvrzení: Sčítání vektorů je komutativní, tedy platí u+v = v+u.
Důkaz: Nejprve si uvědomme, že vektory u+v a v+u jsou si rovny, právě když se shodují v každém koeficientu. A protože tyto koeficienty jsou reálná čísla, přenesou se jejich komutativita i na vektory:
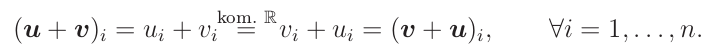

Tento důkaz ilustruje
obecný princip algebry. Matematické struktury jsou definovány tak, že jsou složeny
z jednodušších struktur spolu s přidanými operacemi a vztahy. Pochopitelně tento řetěz někdy musí skončit, tedy nějakou základní strukturu musíme přímo popsat. Situace je podobná jako s ruskými panenkami Matrjoška.
Důležité je, že vlastnosti jednodušších struktur
se přenášejí o hladinu výše na strukturu, která je obsahuje. Například vektory jsou tvořeny reálnými čísly, které vzniknou z podmnožin racionálních čísel, které vzniknou z dvojic celých čísel, které vzniknou jako dvě kopie přirozených čísel. Tedy to, že vektory jsou komutativní je důsledek toho, že přirozená čísla jsou komutativní.
Lemma o výměně
Jednodušší verze Steinitzovy věty. Říká, že je možné nahradit jeden vektor množiny za libovolný nenulový vektor z jejího lineárního obalu.
Lemma: Nechť X je libovolná množina vektorů a y ≠ 0 patří do ⟨X⟩. Potom existuje z∊X takové, že
⟨X \ {z} ∪ {y}⟩ = ⟨X⟩.
Důkaz:
Protože y patří do ⟨X⟩, platí následující:
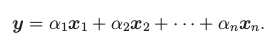
Proto ⟨X⟩ = ⟨X ∪ {
y}⟩ ⊇ ⟨X \ {
z} ∪ {
y}⟩.
Pro druhou inkluzi zvolíme jako
z libovolný vektor
xi, jehož 𝛼
i ≠ 0. Snadnou úpravou ukážeme, že
xi lze vyjádřit pomocí ostatních
xj a
y:
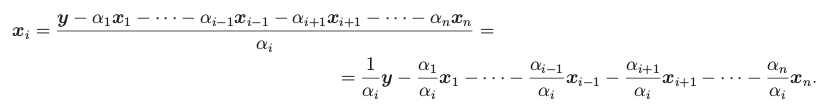
Tedy ⟨X⟩ ⊆ ⟨X \ {
xi} ∪ {
y}⟩.
Faktorprostory
Afinní podprostory jsou zajímavé strukturálně.
Tvrzení: Množina všech afinní podprostorů vzniklých posunutím W tvoří vektorový prostor.
Důkaz: Stačí definovat vektorové operace: (W+p)+(W+q) = W+(p+q) a c*(W+p) = W+c*p. Rozmyslete si, že splňují definice vektorového prostoru.
 Tyto vektorové prostory jsou důležité a říká se jim faktorprostory. Nechť V je vektorový prostor a W je jeho podprostor. Vektorový prostor všech afinních podprostorů vzniklých posunutím W se značí V/W a nazývá se faktorprostor nebo také kvocient.
Tyto vektorové prostory jsou důležité a říká se jim faktorprostory. Nechť V je vektorový prostor a W je jeho podprostor. Vektorový prostor všech afinních podprostorů vzniklých posunutím W se značí V/W a nazývá se faktorprostor nebo také kvocient.
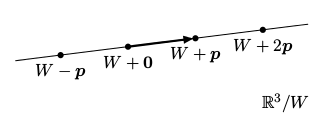
Faktorprostor V/W si můžeme představit tak, že
ve V "splácneme" každý afinní podprostor vzniklý posunutím W
do jednoho vektoru.
Tvrzení: Platí, že dim(W)+dim(V/W) = dim(V).
Lineární obal a generátory
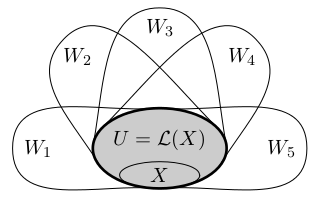
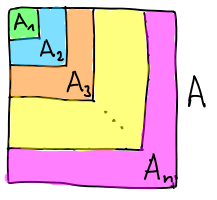
Lineární obal ⟨X⟩ množiny vektorů X je množina všech lineárních kombinací vektorů z X. Podle lemmatu jsou to všechny vektory, které lze získat z X aplikováním konečných posloupností operací. Lineární obal se někdy také značí L(X) nebo span(X). Říkáme, že X generuje ⟨X⟩.
 Pozorování:
Pozorování: Lineární obal ⟨X⟩ je
vektorový podprostor.
Tvrzení:
Lineární obal ⟨X⟩ je nejmenší vektorový podprostor, který obsahuje všechny vektory z X, což je infimum ve svazu podprostorů. Tedy ⟨X⟩ je průnik přes všechny vektorové podprostory, které obsahují X.
 Tagy:
Tagy: #klicove
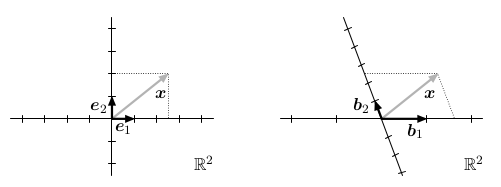
Báze
Množina vektorů se nazývá báze, pokud je lineárně nezávislá a generuje celý prostor. Chceme tedy co nejméně vektorů, které umožnují popsat vektorový prostor. Podobně můžeme báze uvažovat i pro libovolný vektorový podprostor.
Každá báze b1,...,bn definuje systém souřadnic nad vektorovým prostorem:
Pokud x = c1*b1 + ... + cn*bn, jsou jeho souřadnice (c1,...,cn).
Různé báze definují různé systémy souřadnic. Například pro kanonickou bázi vlevo jsou souřadnice vektoru
x rovny (5/2,2), zatímco pro bázi vpravo jsou (8/5,5/2).
Následující vlastnost vyplývá z lineární nezávislosti báze:
Tvrzení: Pro každý vektor
x jsou jeho
souřadnice určené jednoznačně.
Tagy: #klicove
Motivace pro různé báze
Je přirozené se ptát, proč chceme uvažovat různé báze a nevystačíme si s přirozenou kanonickou bází:
- Pro ℝn je přirozené uvažovat kanonickou bázi, protože má speciální roli z pohledu složek vektorů (proto se nazývá kanonická). Avšak pro abstaktní vektorový prostor V žádná přirozená kanonická báze neexistuje. Bází je spousta a není žádná speciální, kterou bychom chtěli vždy zvolit. Tedy je lepší pracovat s teorii obecných bází.
- Řada problémů se mnohem zjednodušší při vhodné volbě báze. Lineární zobrazení je reprezentováno různými maticemi pro různé volby bází. Jedna z klíčových otázek lineární algebry je, jako bázi zvolit, aby byla reprezentující matice co nejjednodušší, což vede na vlastní čísla a třeba dekompozici podle singulárních hodnot SVD. Další příklad je Lagrangeova interpolace.
- Často hledáme vhodnou bázi, která je co nejlepší k popisu dané situace. Například ve statistice můžeme mít data jako vektory v hodně rozměrném prostoru. Hledáme bázi, ve které by bylo možné popsat data co nejjednodušším způsobem, například by se mohlo stát, že skoro všechna leží v nějaké rovině či podprostoru malé dimenze. (I když typicky kvůli chybám měření to nevyjde přesně tak, ale s tím se umí lineární algebra vypořádat přes SVD.) Skvělá metafora jsou procesy se skrytou bází i mimo lineární algebru. To jsou procesy, které jsou na první pohled strašně složité, dokud se neobjeví vhodná skrytá báze, ve které je jejich popis strašně jednoduchý. Třeba pohyb planet je jednoduchý z pohledu univerzální gravitace.
Fibonacciho čísla je posloupnost definovaná následující rekurencí:
f0 = 0, f1 = 1 a fn+2 = fn+1 + fn.
Posloupnost je to zajímavá a splňuje řadu pěkných matematických vlastností. S pomocí volby vhodné báze nalezneme následující vzorec pro n-té Fibonacciho číslo:
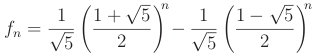
Uvažme prostor všech fibonacciovských posloupností, což jsou posloupnosti splňující rekurenci s libovolnými hodnotami prvních dvou členů (a
0, a
1). Ty tvoří vektorový prostor dimenze dva. Pro ten chceme najít bázi tvořenou posloupnostmi, pro které bude jednoduchý vzorec pro n-tý člen: a
n = x
n pro nějaké reálné číslo x. Protože taková posloupnost musí splňovat rekurenci, platí x
n+2 = x
n+1 + x
n, neboli x
2 = x + 1. Řešením jsou dvě fibonacciovské posloupnosti tvořící bázi prostoru:
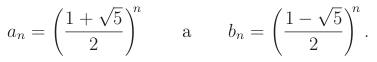
K získání vzorce zbývá dopočítat souřadnice vektoru (0,1): 𝛼 = 1/√5 a 𝛽 = -1/√5:
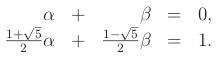
Geometrie vektorů
Vektorový prostor ℝn je tvořen vektory, které geometricky odpovídají bodům. Vznikne obecněním ℝ2 a ℝ3. Pro ně Deckard vymyslel, že sice prostor přímo nevidíme, ale můžeme v něm popisovat pozici pomocí trojice souřadnic (x,y,z).
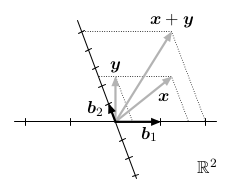
Poznamenejme, že za vektory jsou někdy označovány orientované úsečky. Toto dělení bodů a vektorů je historické a dnes již zbytečné. Někdy s vektorem budeme pracovat jako s bodem, jindy se nám bude hodit interpretace, že je to šipka vycházející z počátku do tohoto bodu.
Násobení skalárem odpovídá natažení vektoru v daném směru. Pokud je koeficient záporný, bude výsledný vektor ukazovat opačným směrem.
Motivace pro sčítání dvou vektorů vychází z fyziky, konkrétně z Newtonovské mechaniky. Pokud vektory reprezentují působení síly (ta má velikost a směr), tak sčítání reprezentuje skládání těchto sil, tedy určení jedné zkombinované síly.
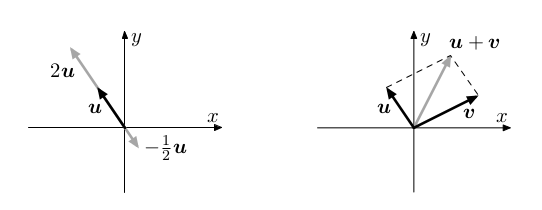
Vektorové podprostory
Vektorový podprostor W je neprázdná množina vektorů uzavřená na operace. To přesně znamená, že kdykoliv u a v patří do W, patří tam také u+v a c*u pro libovolné c. Speciálně počátek 0 vždy patří do W.
Studovat vektorové podprostory je užitečné ze dvou důvodů:- Mají speciální strukturální vlastnosti, například sami o sobě tvoří vektorový prostor.
- Setkáváme se s nimi v lineární algebře na každém rohu.
Geometricky jsou vektorové podprostory ℝn přímky, roviny a jejich vícerozměrná zobecnění procházející počátkem.
Uvažme všechny vektorové podprostory uspořádané inkluzí. Například pro ℝ3 získáme níže uvedený Hasseho diagram:
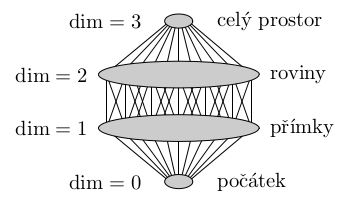
Vidíme, že podprostory jsou rozděleny
do vrstev podle dimenze.
Tvrzení: Vektorové podprostory P tvoří
úplný svaz, což znamená, že pro libovolnou podmnožinu vektorových prostorů
S existuje
infimum a
supremum. Infimum je průnik všech podprostorů v
S, kde průnik přes prázdnou podmnožinu je celý prostor. Supremum se definuje jako infimum všech podprostorů, které obsahují všechny podprostory v
S, tedy jako jejich průnik.
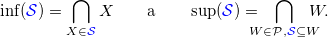
Pokud vám definice suprema pomocí infima připadá podivná, rozmyslete si, že obecně
stačí ukázat existenci pouze infim, nebo pouze suprem, existence toho druhého automaticky vyplývá.
Tagy: #klicove
Lineární kombinace
Výraz c1*x1 + ⋯ + cn*xn se nazývá lineární kombinace vektorů x1,...,xn.
Zároveň se výsledný vektor nazývá lineární kombinace.
Motivace pro studium lineárních kombinací je, že to jsou univerzální operace s vektory:
Tvrzení: Libovolná konečná posloupnost operací je ekvivalentní nějaké lineární kombinaci.
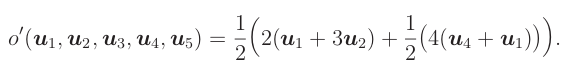
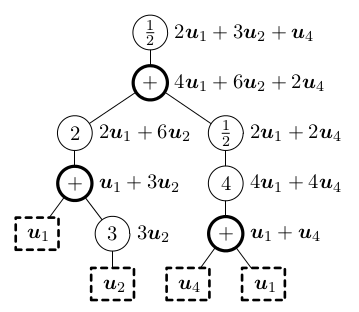 Důkaz:
Důkaz: Indukcí podle stromu posloupnosti operací:
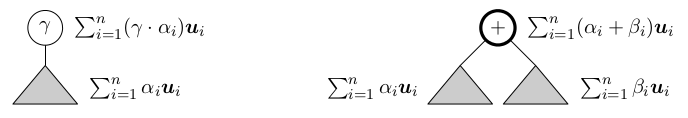 Tagy:
Tagy: #klicove
Řádková interpretace
Mějme soustavu m rovnic o n neznámých. Jednotlivá ohodnocení neznámých můžeme identifikovat s vektory ℝn.
Jak vypadá množina všech řešení geometricky? Můžeme postupovat tak, že určíme množinu řešení Ri pro každý z řádků i=1,...,m. Celá množina řešení soustavy je průnik R1 ∩ ⋯ ∩ Rm.
Příklady soustav 2 rovnic o 2 neznámých: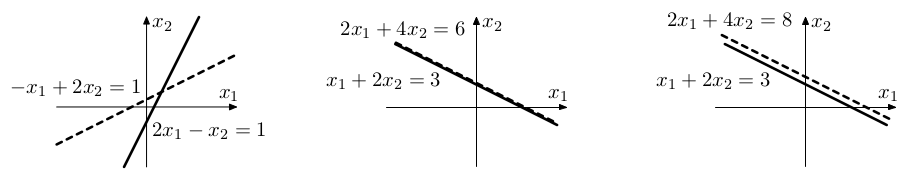 Vlevo je to jeden bod, ležící v průniku dvou přímek. Uprostřed je v průniku celá přímka. Vpravo je prázdný průnik, neboť jsou přímky rovnoběžné.
Jak vypadá množina Ri obecně?
Vlevo je to jeden bod, ležící v průniku dvou přímek. Uprostřed je v průniku celá přímka. Vpravo je prázdný průnik, neboť jsou přímky rovnoběžné.
Jak vypadá množina Ri obecně?
Povšimněme si, že hodnoty libovolných n-1 proměnných můžeme zvolit libovolně, čímž je hodnota zbývající proměnné jednoznacně určena.
Tedy Ri má n-1 "stupňů volnosti".
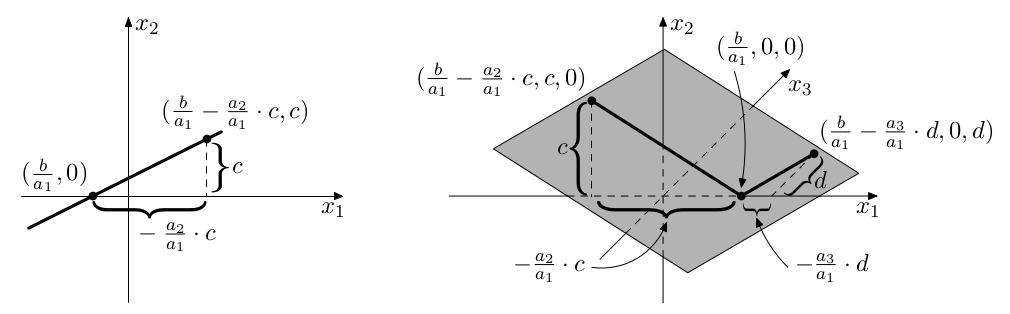
Geometricky Ri tvoří nadrovinu posunutou z počátku, což je afinní podprostor dimenze n-1, zobecnění rovin v ℝ3. Koeficienty ai,1,...,ai,n určují směr normálového vektoru, který je kolmý k nadrovině. Koeficient bi určuje posunutí nadroviny z počátku.
Abychom toto mohli dokázat, museli bychom mít jinou geometrickou definici nadroviny.
Zkuste si však rozmyslet, že to tak funguje pro malé hodnoty n. Konkrétně pro n=2 (vlevo) dostaneme přímku posunutou z počátku, pro n=3 (vpravo) získáme rovinu posunutou z počátku.
Tagy: #klicove
Vektorové prostory
Jeden z pohledů na lineární algebru je ten, že je to studium vektorových prostorů a jejich transformací (lineární zobrazení). Vektorové prostory jsou proto jedny z nejzákladnějších struktur v matematice. Jsou tvořené body, které se nazývají vektory, a tyto vektory umíme aplikovat dvě operace: sčítání a násobení skalárem.
Jsou dva možné přístupy, jak lze vektorový prostor definovat. (A ty obecně odpovídají dvěma rozdílným přístupům, jak lze v matematice popisovat objekty.) První je konstrukcí, kdy přesně specifikujeme, co jsou vektory a jak se na ně aplikují operace. Druhý abstraktní postup je přes popis vlastností. Řekneme, že vektorový prostor je tvořen nějakou množinou vektorů spolu s operacemi, které splňují daný seznam vlastností.
Jsou dva možné způsoby, jak lze definovat vektorový prostor.
Konkrétní konstrukce:
Vektorový prostor ℝn je tvořen n-ticemi x = (x1,...,xn), zvanými vektory, spolu s operacemi sčítání a násobení skalárem definovaných po složkách:
- x+y = (x1+y1,...,xn+yn).
- c*x = (c*x1,...,c*xn).
Abstraktní definice: Vektorový prostor je tvořen nějakou množinou prvků, kterým se říká vektory, spolu s operacemi sčítání + a násobení skalárem *, které splňují následující vlastnosti:
- Komutativita +: u+v = v+u.
- Asociativita +: u+(v+w) = (u+v)+w.
- Neutrální prvek +: Existuje vektor 0 takový, že u+0=u pro každý vektor u.
- Inverzní prvky +: Pro každý vektor u existuje vektor (-u) takový, že u+(-u) = 0.
- Asociativita *: (a*b)*u = a*(b*u).
- Neutrální prvek *: 1*u = u.
- První distributivita: (a+b)*u = (a*u) + (b*u).
- Druhá distributivita: a*(u+v) = (a*u) + (a*v).
Tagy: #klicove
Lagrangeova interpolace
K vyřešení interpolace chceme najít vektor koeficientů a na prostoru polynomů ℙn stupně nejvýše n. Najít jeho souřadnice vůči kanonické bázi je obtížné a vede to řešení soustavy
 Vn+1a = y.
Vn+1a = y.
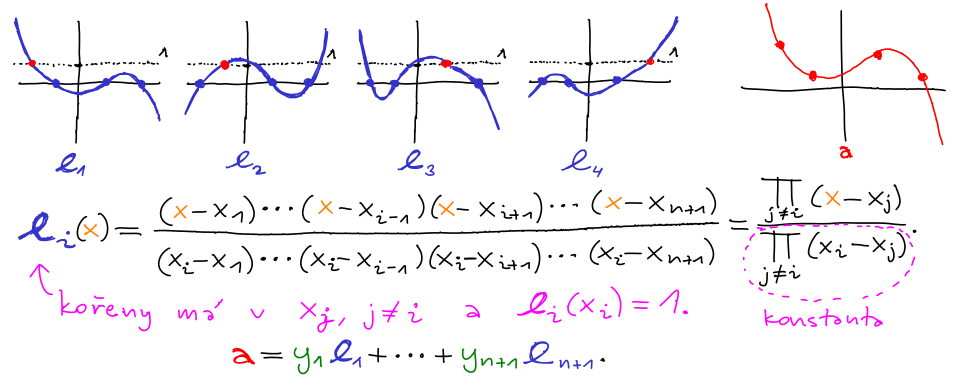
Lagrangeova interpolace je založena na myšlence, že
problém se stane velice jednoduchý při volbě vhodné báze ℓ1, ...,
ℓn+1.
Bázi ℓ1, ..., ℓn+1 zvolíme, aby každý z vektorů ℓi interpoloval jeden z bodů (xi, yi). Jejich jednoduchou lineární kombinací získáme hledaný vektor a.
Podle
Steinitzovy věty víme, že
ℓ1, ...,
ℓn+1 je báze. Její existence
dokazuje větu o jednoznačnosti polynomu P(x) stupně n procházejícího body (x
1,
y1), ..., (x
n+1,
yn+1).
Samozřejmě je možné volit i jiné báze. Jedním příkladem je
Newtonova interpolace, vůči bázi
n1, ...,
nn+1. Ta funguje skvěle na přidávání dalších bodů, neboť vektor
ni závisí pouze na bodech (x
1,
y1), ..., (x
i,
yi).
Geometrické příklady ℝ² → ℝ²
Řada geometrických zobrazení f : ℝ2 ⟶ ℝ2 splňuje linearitu:- natažení,
- rotace,
- zkosení,
- projekce a
- jejich kombinace.
Příklad nelineárního geometrického zobrazení f : ℝ2 ⟶ ℝ2 je posunutí ℝ2 o libovolný nenulový vektor x.
Natažení: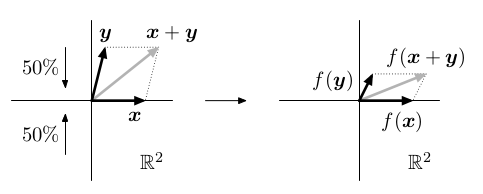
Rotace: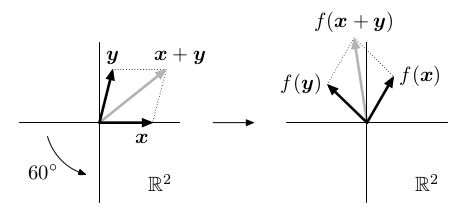 | Zkosení: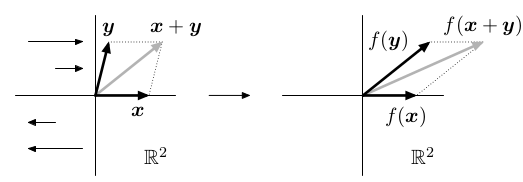
Kolmá projekce: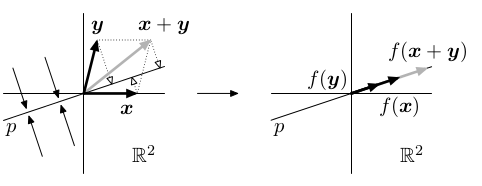 |
Geometrie elementárních úprav
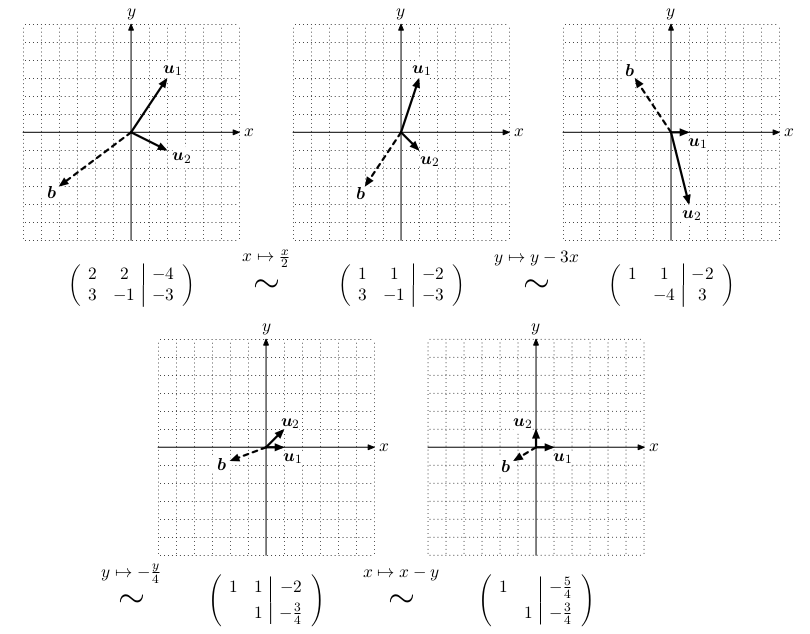
Řádkové úpravy z pohledu sloupcové interpretace:
Řádkové úpravy transformují prostor ℝm spolu s vektory u1,...,un a pravou stranou b. Klíčová vlastnost je, že pokud úprava prostor nikde nesplácne (tedy je regulární), je vztah mezi u1,...,un a pravou stranou b zachován.
Elementární řádkové úpravy odpovídají následujícím geometrickým transformacím prostoru ℝm:
- Násobení i-tého řádku skalárem 𝛼 odpovídá 𝛼-násobnému natažení prostoru ve směru i-té souřadné osy.
- Přičtení i-tého řádku k j-tému odpovídá zkosení i-té souřadné osy do j-té souřadné osy.
V maticovém zápisu, nechť R je regulární matice řádkových úprav reprezentující geometrickou transformaci. Ze soustavy lineárních rovnic Ax=b získáme transformovanou soustavu RAx=Rb.
Sloupcové úpravy z pohledu sloupcové interpretace:
Sloupcová úprava transformuje jednotlivé sloupcové vektory u1,...,un. Jejich vztah k pravé straně b se může změnit, tedy mění se množina všech řešení. Je možné provádět sloupcové úpravy, ale musíme si je zapamatovat a na závěr příslušně upravit nalezené řešení.
Elementární sloupcové úpravy odpovídají následujícím transformacím:
- Násobení i-tého sloupce skalárem 𝛼 odpovídá 𝛼-násobnému natažení vektoru ui.
- Přičtení i-tého sloupce k j-tému odpovídá zkosení ui do uj.
V maticovém zápisu, nechť S je regulární matice sloupcové úpravy reprezentující transformaci sloupcových vektorů. Ze soustavy lineárních rovnic Ax=b získáme transformovanou soustavu ASS-1x=b, která vede na soustavu ASy=b. Když ji vyřešíme a nalezneme hodnotu y, musíme dopočítat x=Sy.
Geometrická struktura množiny všech řešení
Věta: Množina všech řešení soustavy Ax=0 je vektorový podprostor, který se značí Ker(A).
Důkaz: Stačí ukázat, že množina všech řešení je uzavřená na sčítání a násobení skalárem. Když x je řešením soustavy Ax=0, platí pro i-tou rovnici:
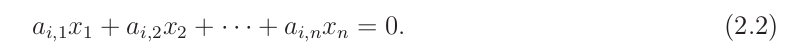
Množina řešení je uzavřená na sčítání, neboť se zachovává se splnění i-té rovnice:
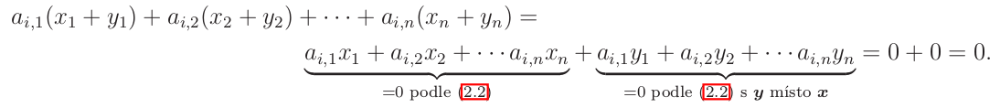
Důkaz uzavřenosti na násobení je podobný.
V maticovém zápisu je to ještě jednodušší. Pokud Ax=0 a Ay=0, potom
A(c*x) = c*(Ax)=c*0=0 a A(x+y) = Ax+Ay = 0+0 = 0.Věta: Množina všech řešení soustavy Ax=b je afinní podprostor Ker(A)+p, kde p je libovolné řešení soustavy.
Důkaz: Stačí si všimnout, že kdykoliv máme dvě řešení Ax=b a Ay=b, jejich rozdíl x-y patří do Ker(A):
A(x-y) = Ax-Ay = b-b = 0.
Zbytek plyne z vlastností afinních podprostorů.
Klíčový důsledek: Uvažme různé pravé strany
b. Pro některé nebude existovat žádné řešení, což odpovídá neexistence vektoru
p. Pro ty zbývající jsou to afinní podprostor vzniklé různými posunutími Ker(A). Tedy množiny řešení soustav A
x=
b a A
x=
c mají totožnou strukturu až na posunutí.
Označíme Im(A) množinu všech pravých stran, pro kterou existuje řešení, to je vektorový podprostor
ℝ
m (neboť afinní podprostory vzniklé posunutím W tvoří vektorový prostor). Platí, že
čím větší je Ker(A), tím méně jeho posunutí existuje, tedy
tím méně pravých stran má řešení.
Tento vztah lze přesně popsat pomocí dimenzí:dim Ker(A) + dim Im(A) = n.Tagy: #klicove
Sloupcová interpretace
I když se tato interpretace často ignoruje, považuji ji za mnohem užitečnější než tu řádkovou. Myšlenka je, že budeme uvažovat sloupcové vektory matice a pravé strany, které patří do ℝm:
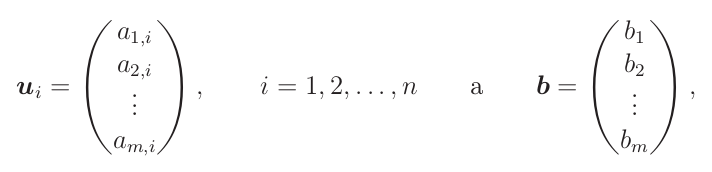
Nyní učiníme klíčové pozorování, že se neznámá x
i objevuje přesně u koeficientů jednoho sloupcového vektoru
ui. Tedy soustava lineárních rovnic je
ekvivalentní s vektorovou rovnicí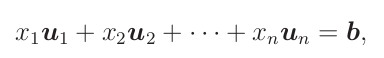
kde rovnost má platit v každé složce.
Tedy máme rovnici
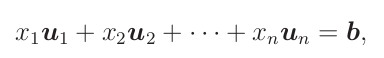
kterou chceme interpretovat geometricky. Hledáme koeficienty x
1,...,x
n natažení vektorů
u1,...
un, tak aby se zkombinovali pravou stranu
b.
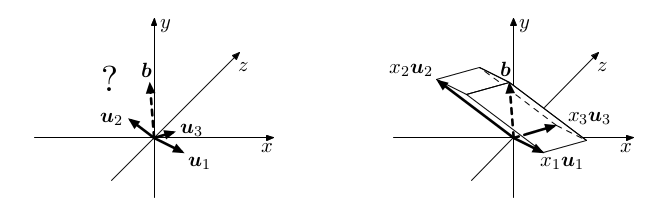
Voleb koeficientů může být spousta, což vede k nekonečně mnoha řešením. Pokud vektory
u1,...
un ukazují "jiným" směrem než
b, soustava nemá žádné řešení.
Tagy: #klicove
Interpolace polynomů
Soustavami lineárních rovnic lze rešit problém, který s nimi na první pohled vůbec nesouvisí. Uvažme polynomy
P(x) = an*xn + an-1*xn-1 + ⋯ + a1*x + a0.
stupně n. Platí následující algebraická věta, úzce související s fundamentální větou algebry.
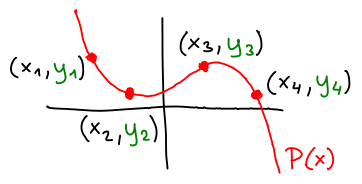 Věta:
Věta: Existuje
právě jeden polynom P(x) stupně n, který prochází libovolnými n+1 body
(x1,y1), ..., (xn+1,yn+1),
kde x
i ≠ x
j pro i ≠ j, tedy P(x
i) =
yi.
Hledání koeficientů tohoto polynomu se nazývá
interpolace polynomů a je možné to udělat vyřešením
soustavy lineárních rovnic.
K nalezení koeficientů stačí vyřešit následující soustavu, kde y = (y1, ..., yn+1) a vektor a je vektor hledaných koeficientů polynomu P(x).
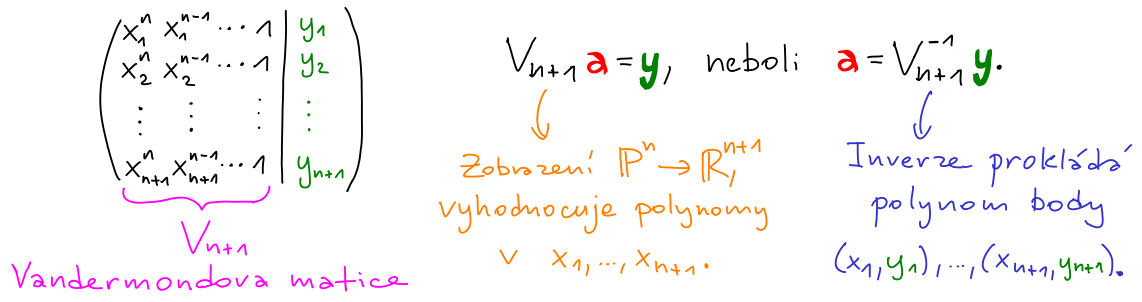
Větu o jednoznačnosti interpolace je možné dokázat pomocí lineární algebry. Stačí dokázat, že
Vandermondova matice Vn+1 je regulární, právě když x
i ≠ x
j pro i ≠ j. Jiný důkaz vyplývá z
Lagrangeovy interpolace.
Maticová reprezentace f : x ↦ A x
Věta:
Libovolné lineární zobrazení f : U ⟶ V je reprezentováno maticí tak, že f : x ↦ Ax, tedy f(x) = Ax.
Důkaz: Zobrazení x ↦ Ax je vždy lineární zobrazení z distributivity maticového násobení: A(x+y) = Ax + Ay a A(c*x) = c*(Ax).
Na druhou stranu, zobrazení f : ℝn ⟶ ℝm je z linearity jednoznačně popsané obrazy f(e1), ..., f(en):
Pro x = (x1, ..., xn) = x1*e1 + ⋯ + xn*en je f(x) = x1*f(e1) + ⋯ + xn*f(en).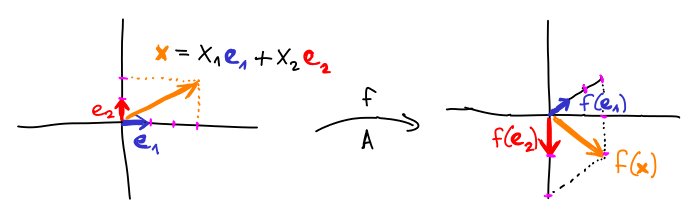
Každý z obrazů f(
ei) má m souřadnic, dohromady je tedy f jednoznačně určené pomocí m x n souřadnic, které zapíšeme po sloupcích do tabulky A zvané matice.
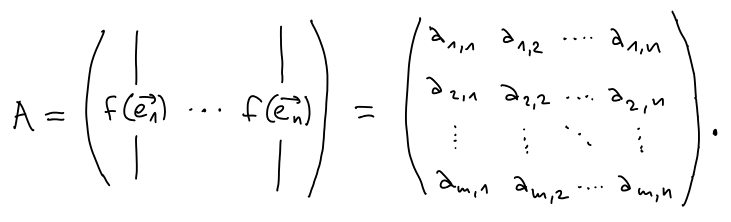
Z definice maticového násobení je A
x = x
1*f(
e1) + ⋯ + x
n*f(
en), tedy f(
x) = A
x.
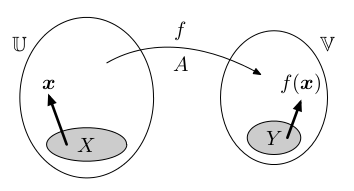 Víme, že lineární zobrazení f : U ⟶ V je jednoznačně určeno obrazy libovolné báze. Zvolíme libovolně dvě báze:
Víme, že lineární zobrazení f : U ⟶ V je jednoznačně určeno obrazy libovolné báze. Zvolíme libovolně dvě báze:
- X = {x1,...,xn} jako bázi prostoru U,
- Y = {y1,...,ym} jako bázi prostoru V.
K popisu zobrazení stačí znát f(x1),...,f(xn), kde každý z těchto obrazů lze popsat pomocí m souřadnic vůči bázi Y.
Rozhodneme se zapsat těchto m x n souřadnic do tabulky A, které budeme říkat matice. Souřadnice jednotlivých vektorů f(xi) zapíšeme do sloupců:
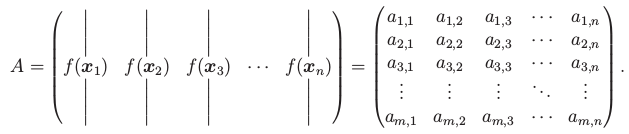
Tedy a
i,j je souřadnice f(
xj) vůči
yi.
Věta: Nechť A je maticová reprezentace f a nechť
x je vyjádřený vůči bázi X. Potom jsou souřadnice f(
x) vůči bázi Y ve vektoru A
x. Tedy f :
x ↦ A
x.
Klíčové: Pro
různé volby bází X a Y můžeme získat různé maticové reprezentace lineárního zobrazení f. Naopak
jedna matice může reprezentovat různá lineární zobrazení pro různou volbu bází.
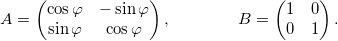
Například uvažme rotaci o úhel 𝜑 v rovině. Ta je reprezentovaná maticí A, pokud X=Y je kanonická báze tvořená vektory (1,0) a (0,1). Pokud však X je kanonická báze a Y je X otočená o úhel 𝜑, je rotace reprezentovaná maticí B. Na druhou stranu, pokud X=Y a zobrazení je endomorfismus, reprezentuje matice B identické zobrazení.
Tagy: #klicove
Derivace a integrál
Geometrie Gaussovy eliminace
Gaussova eliminace provádí geometrické transformace sloupcových vektorů a pravé strany elementárními řádkovými úpravami. Převede soustavu do odstupňovaného tvaru se sloupcovými vektory u1,...,un a pravou stranou b, ve kterém je snadné ji vyřešit.
Pokud b ukazuje jiným směrem než sloupcové vektory, poznáme to podle toho, že ukazuje ve směru souřadné osy, která není obsažena v žádném ze sloupcových vektorů u1,...,un. Tedy b nelze vyjádřit pomocí sloupcových vektorů u1,...,un a řešení soustavy neexistuje.
Pokud jsou všechny tyto koeficienty b nulové, řešení existuje. Najdeme ho tak, že hodnoty volných proměnných zvolíme libovolně, čímž známe natažení příslušných sloupcových vektorů. Můžeme je odečíst od pravé strany a získat upravenou pravou stranu b'. Pro sloupcové vektory s pivoty dopočteme hodnotu řešení, protože vždy pouze jeden z nich ukazuje určitým směrem b', tedy jeho hodnota natažení je jednoznačně určena a lze příslušný sloupcový vektor odečíst.
Věta o homomorfismu
Věta: Pro libovolné lineární zobrazení f : U ⟶ V platí, že
U / Ker(f) ≅ Im(f).
Víme, že vzorem jednotlivých vektorů z Im(f) jsou afinní podprostory U vzniklé posunutím Ker(f). Tedy vzory jednotlivých vektorů z Im(f) mají stejnou strukturu až na posunutí.
Platí, že
čím větší je Ker(f), tím méně jeho posunutí existuje, tedy
tím méně vzorů má řešení.
Přesněji, ve řeči dimenzí:dim Ker(f) + dim Im(f) = dim(U).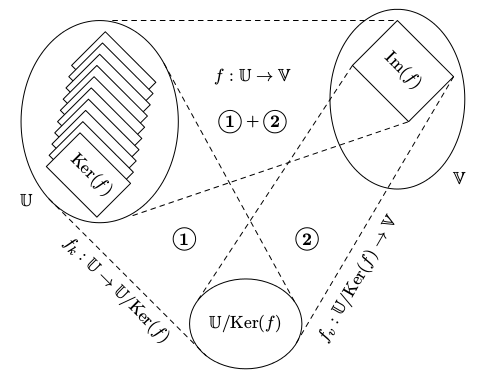 Podle věty lze homomorfismus f : U ⟶ V rozdělit na složení dvou jednodušších homomorfismů:
Podle věty lze homomorfismus f : U ⟶ V rozdělit na složení dvou jednodušších homomorfismů:
- Kvocientový homomorfismus
fk : U ⟶ U / Ker(f), který je na a obecně není prostý. - Vnořovací homomorfismu
fv : U / Ker(f) ⟶ V, který je prostý, ale obecně není na.
Maticový zápis
Můžeme zjednodušit zápis soustavy tak, že vynecháme zbytečné informace:
- V jednotlivých sloupcích jsou stejná jména proměnných, která vynecháme.
- Odstraníme operace + a =.
Pro řešení soustavy jsou důležité pouze koeficienty, které zapíšeme do tabulky zvané matice.
Původní soustava: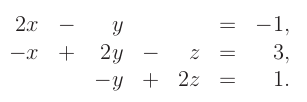 | | Maticový zápis: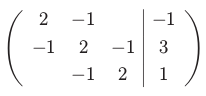 |
Soustavu lze v řeči matic a vektorů vyjádřit v elegatní formě Ax=b. Zde A je matice koeficentů, x je vektor neznámých a b je vektor pravých stran.
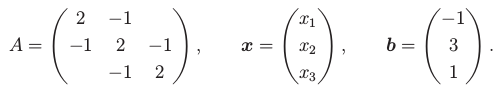
Rozepsáním
definice maticového násobení získáme soustavu lineárních rovnic.
Interpretace
maticového násobení po sloupcích A vede na sloupcovou interpretaci soustavy.
Tagy: #klicove
Věta o izomorfismu
Věta: Libovolný vektorový prostor V dimenze n je izomorfní vektorovému prostoru ℝn.
Slovo izomorfní znamená, že existuje izomorfismus f : V ⟶ ℝn. Ten zaručuje, že algebraická struktura prostorů V a ℝn je totožná, tedy struktura jejich operací. Platí f(x+y) = f(x)+f(y), podobně pro násobení, tedy jednotlivé vektory x prostoru V lze identifikovat s vektory f(x) prostoru ℝn.
Neznamená to, že by tyto prostory byly totožné, například V může být prostor polynomů stupně nejvýše n-1, a tedy jeho prvky jsou úplně jiné matematické objekty než n-tice reálných čísel. Avšak izomorfismus říká, že v řadě situací můžeme pracovat s V přesně jako s ℝn, například lze řešit soustavy nad ℝn místo nad abstraktním prostorem V.
Důkaz: Zvolíme libovolnou bázi prostoru V. Ta definuje souřadnice (c1,...cn) nad V. Tato definice souřadnic je hledaný izomorfismus:
f : c1*b1 + ... + cn*bn ⟼ (c1,...,cn).
Protože souřadnice jsou definované pro každý vektor V jednoznačně, je definované zobrazení bijekce. Zbývá ověřit, že to skutečně je lineární zobrazení. Stačí si všimnout, že sčítání vektorů ve V odpovídá sčítání jejich souřadnic, podobně pro skalární násobení.
 Tagy:
Tagy: #klicove
Analýza dynamických systémů
Velká část matematiky se zabývá studiem modelů reálného světa. To jsou často dynamické systémy, jejichž stav (například vektor reálných čísel) se mění v závislosti na čase. Změna stavu je popsána matematickými vztahy, například lokálně diferenciálními rovnicemi. Při analýze chceme odpovídat na otázky následujícího typu: predikce vývoje z počátečního stavu, pochopit kvalitativní chování (konvergence k ustálenému stavu, oscilace, chaotické chování).
Problém je, že typický dynamický systém je příliš složitý a nemůže být přesně popsán jeho vývoj. Ve většině situací se spokojíme s tím, že nalezneme přibližné řešení jeho diskretizací (simulace, metoda konečné mřížky, metoda konečných prvků), čímž se v řadě situací převede na řešení velké soustavy lineárních rovnic
Ax=b.
Zde matice A popisuje zdiskretizované vztahy v systému, zatímco vektor
b odpovídá stavu nebo vývoji stavu. Při řešení se často využívá specifické struktury koeficientů matice A.
Historie
Řešení soustav lineárních rovnic je odvěký problém se spoustou aplikací. Konkrétní soustavy lineárních rovnic se v matematice objevují již před více než pěti tisíci lety. V čínské knize Devět kapitol napsané zhruba dvě stě let před naším letopočtem se objevuje postup, jak
vyřešit konkrétní soustavu tří lineárních rovnic o třech neznámých. Jakékoliv formální zdůvodnění chybí, ale při zobecnění dostaneme Gaussovu eliminaci.
V západní matematice Gaussovu eliminaci poprvé popsal Newton ve své algebraické knize, i když se jednalo o postup mezi matematiky běžně známý.
Gauss se zabýval metodou nejmenších čtverců (v souvislosti s geodézií), pro níž popsal algoritmus podobný Gaussově eliminaci. Jméno Gaussova eliminace se začalo používat až v padesátých letech díky implementaci metody nejmenších čtverců v počítačích. Historie řady pojmů lineární algebry je značně složitá!Regulární matice
Čtvercová matice se nazývá regulární, pokud je invertovatelná. Ostatní čtvercové matice se nazývají singulární. O inverzích regulárních matic platí následující věta:
Věta: Pro čtvercovou matici existuje levá inverze, právě když existuje pravá inverze. Navíc jsou stejné a určené jednoznačně.
Těžká je první část, která je speciální případ rovnosti rank(A) = rank(AT). Druhá část snadno vyplývá z asociativity. Pokud X je levá inverze a Y je pravá inverze, platí:
X = XIm = X(AY) = (XA)Y = InY = Y.
Tagy: #klicove
Matice
Matice je tabulka m x n reálných čísel:
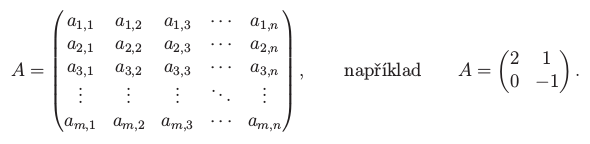
Matice velikosti m x n popisuje geometrickou transformaci vektorového prostoru ℝn do vektorového prostoru ℝm.
Pro matici A označme (A)i,j = ai,j koeficient v i-tém řádku a j-tém sloupci. Řádky matice tvoří řádkové vektory ℝn, sloupce tvoří sloupcové vektory ℝm.
Základní maticové operace jsou násobení skalárem a sčítání:

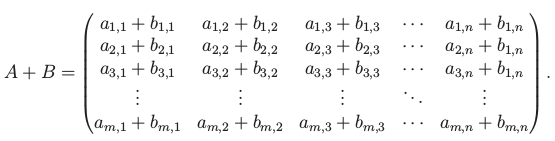
Všechny matice velikosti m x n proto tvoří
vektorový prostor ℝm x n.
Tagy: #klicove
Hledání vzorů
Nechť f : U ⟶ V je lineární zobrazení a b je libovolný vektor V. Chceme nalézt množinu vzorů
f-1(b) = {x : f(x) = b}.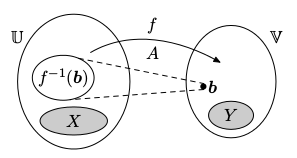 Nechť lineární zobrazení f je reprezentováno maticí A. Víme, že f : x ↦ Ax. Tedy hledáme všechny vektory x, které splňují Ax = b, což vede na soustavu lineárních rovnic. Tedy i kdybychom lineární algebru budovali abstraktně, od vektorových prostorů a jejich homomorfismů, je řešení soustav lineárních rovnic klíčové.
Nechť lineární zobrazení f je reprezentováno maticí A. Víme, že f : x ↦ Ax. Tedy hledáme všechny vektory x, které splňují Ax = b, což vede na soustavu lineárních rovnic. Tedy i kdybychom lineární algebru budovali abstraktně, od vektorových prostorů a jejich homomorfismů, je řešení soustav lineárních rovnic klíčové.
Víme, že množina vzorů f-1(b) je neprázdná, právě když b ∊ Im(f). V takovém případě je to afinní podprostor Ker(f)+p, kde p je libovolný vzor b.
Tagy: #klicove
Lineární zobrazení (homomorfismy)
Nechť U a V jsou dva vektorové prostory.
Zobrazení f : U ⟶ V je lineární, pokud splňuje:

Lineární zobrazení f
vnořuje strukturu U do struktury V. Například pokud platí libovolná rovnost
x +
y =
z, platí i pro jejich obrazy: f(
x) + f(
y) = f(
z). Poznamenejme, že obrazy rovností mohou být velice triviální.
Lineární zobrazení se nazývají
homomorfismy.
Homomorfismy se uvažují nad obecnými matematickými strukturami a jejich zkoumání je velice důležité.
Název se skláda z
homo (zachovávání struktury) a
morfismus (transformace jedné struktury v druhou).
Učiňme nejprve pozorování, že pro libovolné lineární zobrazení f platí, že f(0) = 0. Obrazem počátku musí být počátek z linearity:
f(0) = f(0*0) = 0*f(0) = 0.
Podobně platí následující:
Tvrzení: Obrazem libovolné lineární kombinace je lineární kombinace obrazů. Proto je
lineární zobrazení jednoznačně určené obrazy libovolné báze.
Důkaz: Využijeme linearitu:
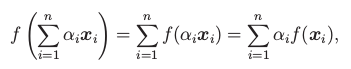 Tagy:
Tagy: #klicove
Skládání zobrazení
Mějme lineární zobrazení f : U ⟶ V a g : V ⟶ W. Existuje složené zobrazení g ∘ f : U ⟶ W, které je také lineární. Jak vypadá jeho maticová reprezentace?
Věta: Nechť
A reprezentuje f : U ⟶ V vůči bázím X a Y,B reprezentuje g : V ⟶ W vůči bázím Y a Z.
Potom
BA reprezentuje g ∘ f : U ⟶ W vůči bázím X a Z.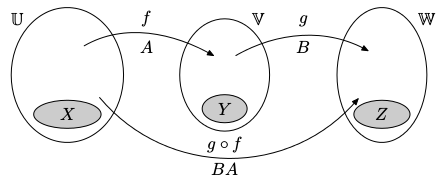 Tato věta vysvětluje definici maticového násobení. Matice musíme násobit tak zvláštně právě proto, aby jejich násobení odpovídalo skládání lineárních zobrazení. Pokud bychom lineární algebru budovali od lineárních zobrazení, můžeme z definice maticové reprezentace odvodit definici maticového násobení.
Tato věta vysvětluje definici maticového násobení. Matice musíme násobit tak zvláštně právě proto, aby jejich násobení odpovídalo skládání lineárních zobrazení. Pokud bychom lineární algebru budovali od lineárních zobrazení, můžeme z definice maticové reprezentace odvodit definici maticového násobení.
Proto také definice maticového násobení vyžaduje kompatibilní rozměry. Nechť A je velikosti n x p, reprezentující zobrazení ℝp ⟶ ℝn, a B je velikosti m x n, reprezentující zobrazení ℝn ⟶ ℝm. Potom je prostor uprostřed totožný, tedy má i stejnou dimenzi, a složené zobrazení ℝp ⟶ ℝm je reprezentováno maticí BA velikosti m x p.
Důkaz z definice: Matice reprezentující g ∘ f vůči bázím X a Z musí mít v i-tém sloupci souřadnice g(f(xi)) vůči bázi Z. Povšimneme si, že v i-tém sloupci matice A máme souřadnice f(xi) vůči bázi Y, a obrazy jednotlivých vektorů báze Y jsou ve sloupcích B. Tedy souřadnice g(f(xi)) vůči bázi Z získáme jako zkombinování sloupců B podle souřadnic v i-tém sloupci A, což přesně odpovídá maticovému násobení.
Důkaz z asociativity: Z asociativity maticového násobení víme, že (BA)x = B(Ax) pro libovolný vektor x. Pravá strana odpovída složenému zobrazení g ∘ f : x ↦ B(Ax). Protože rovnost platí pro libovolný vektor x, musí být g ∘ f reprezentováno BA.
Poznamenejme, že naopak z této věty vyplývá asociativita maticového násobení. To totiž odpovídá skládání lineárních zobrazení, a skládání libovolných zobrazení je asociativní.
Tagy: #klicove
Matice přechodu
Čtvercová regulární matice reprezentující identitu se nazývá matice přechodu. Přepočítává souřadnice od jedné báze X k jiné bázi X'.
Čtvercová regulární matice může reprezentovat různá lineární zobrazení. Pokud zvolíme jednu bázi X, dostáváme nějaký endomorfismus. Lze ji však uvažovat jako reprezentace identity vůči volbě bází X a X'.
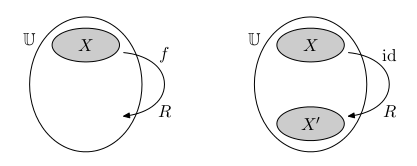
Pokud
x jsou souřadnice vektoru vůči bázi X, jsou A
x souřadnice stejného vektoru vůči bázi X'.
Příklady eliminací
Dopředná eliminace:
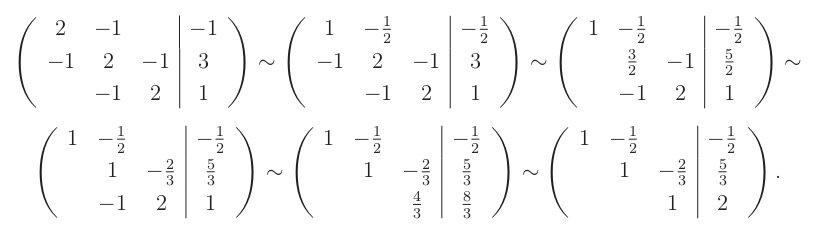
Zpětná substituce:- Nejprve určíme z=2.
- Poté dosadíme za z do druhé rovnice a určíme y=3.
- Nakonec dosadíme za y a z do první rovnice a získáme x=1.
Tedy existuje jednoznačné řešení soustavy (1,3,2).
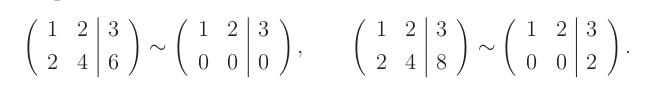 Soustava vlevo:
Soustava vlevo:
Má nekonečně mnoho řešení ve tvaru (3-2y,y), kde y je libovolné reálné číslo. Lze popsat také jako (3,0) + y*(-2,1).
Soustava vpravo:
Neexistuje žádné řešení, neboť jsme úpravami odvodili, že musí platit 0x+0y=2, což není splněno pro žádnou dvojici (x,y) reálných čísel.
Gaussova eliminace
Algoritmus na řešení soustavy lineárních rovnic. Jedná se o strategii, jak aplikovat elementární úpravy tak, aby se matice zjednodušila do odstupňovaného tvaru.
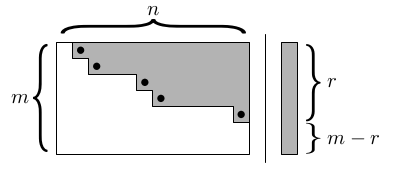
Černě vyznačené koeficienty se nazývají
pivoti a jsou to první nenulové hodnoty na jednotlivých řádcích.
Gaussova eliminace se skládá ze dvou fází:
- dopředná eliminace, která vypočítá odstupňovaný tvar,
- zpětná substituce, která nalezne všechna řešení z odstupňovaného tvaru.
Odstupňovaný tvar je konstruován v n krocích, celkově k jeho spočítání potřebujeme n3/3 elementárních operací (násobení, sčítání).
Stav na počátku i-tého kroku:
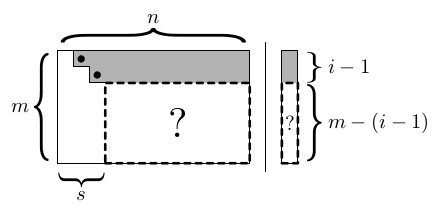 V i-tém kroku se aplikují následující elementární úpravy:
V i-tém kroku se aplikují následující elementární úpravy: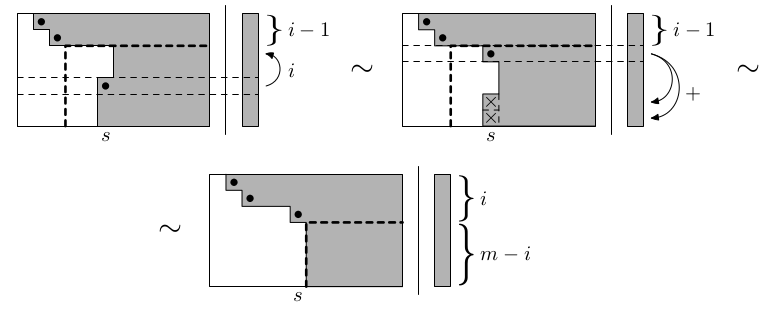 Tagy:
Tagy: #klicove
Podobnost
Dvě matice A a B jsou ekvivalentní, pokud reprezentují stejné lineární zobrazení pro různou volbu bází. Jsou ekvivalentní, právě když existují dvě regulární matice R a S (přechodu), pro které platí:
A = SBR, neboli B = S-1AR-1.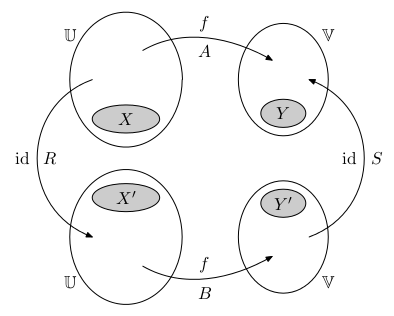 Podobnost je maticová ekvivalence pro čtvercové matice reprezentující endomorfismy vůči jedné bázi. Tedy dvě matice A a B jsou podobné, právě když reprezentují stejný endomorfismus pro jinou volbu báze. To je právě tehdy, když existuje regulární matice R (matice přechodu), že platí:
Podobnost je maticová ekvivalence pro čtvercové matice reprezentující endomorfismy vůči jedné bázi. Tedy dvě matice A a B jsou podobné, právě když reprezentují stejný endomorfismus pro jinou volbu báze. To je právě tehdy, když existuje regulární matice R (matice přechodu), že platí:
A = R-1BR, neboli B=RAR-1.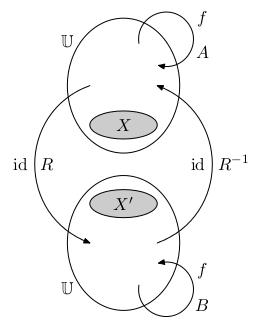
Matice úprav
Regulární úpravy odpovídají regulárním maticím.
Soustava Ax=b se upraví na soustavu RAx=Rb, kde R je nějaká regulární matice.
Tvrzení: Pokud R je regulární matice, je množina řešení Ax=b a RAx=Rb je stejná.
Důkaz:
Pokud x řeší původní soustavu, určitě také řeší upravenou soustavu. Tedy množina řešení se může každou úpravou pouze zvětšit. Protože je R regulární, existuje inverzní úprava R-1, která převede upravenou soustavu zpět do původního stavu:
R-1RAx = R-1Rb ⟹ Ax = b.
Proto musí být
množina řešení stejná, jinak by se úpravou R
-1 zmenšila, což není možné.
Regulární matice R elementárních řádkových úprav jsou velice jednoduché. Vlevo je přičtení i-tého řádku k j-tému. Vpravo je vynásobení i-tého řádku koeficientem 𝛼 ≠ 0.
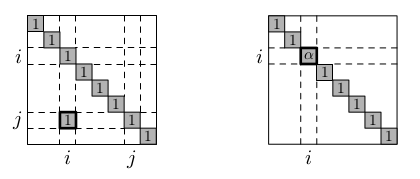
Čtenář si může rozmyslet, jak vypadají matice odvozených elementárních úprav: přičtení 𝛼-násobku i-tého řádku k j-tému a prohození dvou řádků.
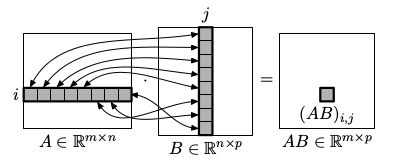
Maticové násobení
Nechť A∊ℝm x n a B∊ℝn x p. Potom je součin AB matice velikosti m x p s následujícími koeficienty:
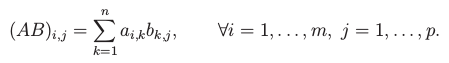
 Příklad maticového součinu: (vlevo A, nahoře B)
Příklad maticového součinu: (vlevo A, nahoře B)

Toto je
pohled řádek-sloupec na maticové násobení. Existují však ještě tři další užitečné pohledy:
- Pohled sloupec-sloupec: Nejprve se zaměřme na součin Ax. (Zde s vektorem pracujeme jako s maticí, co má jeden sloupec.) Podle definice jsou jednotlivé sloupcové vektory u1,...,un matice A násobeny jednotlivými koeficienty vektoru x a sečteny. Tedy dostáváme lineární kombinaci
Ax = x1*u1 + ⋯ + xn*un.
Matice AB obsahuje jako sloupcové vektory lineární kombinace sloupcových vektorů A s koeficienty podle sloupcových vektorů B. - Pohled řádek-řádek: Identický s předchozím, pouze transponovaně, získáváme lineární kombinace řádků B podle koeficientů matice A.
- Pohled sloupec-řádek: V definici součinu vždy koeficienty i-tého sloupce matice A násobí pouze koeficienty i-tého řádku matice B. S využitím distributivity lze tedy spárovat sloupce x1,...,xn matice A s řádky y1T,...,ynT matice B. Dostáváme následující součet n matic m x p:
AB = x1 y1T + ⋯ + xnynT.
Tagy: #klicove, #nasobeni_matic
Endomorfismy, izomorfismy, automorfismy
Používají se tři prefixy pro speciální druhy homorofismů: endomorfismy, izomorfismy a automorfismy. Ty rozlišují jestli je f zobrazení obecné nebo bijektivní, a jestli f zobrazuje mezi dvěma prostory U a V, nebo z prostoru U do téhož prostoru U.
| f : U ⟶ V | f : U ⟶ U |
| obecně | homomorfismus | endomorfismus |
| f je bijekce | izomorfismus | automorfismus |
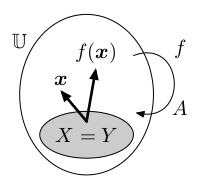 Každý endomorfismus je homomorfismus a každý automorfismus je izomorfismus, ale jména specificky zdůrazňují, že je uvažujeme jako zobrazení z jednoho prostoru do téhož prostoru. Složení endomorfismů jsou endomorfismy, navíc je lze mocnit:
Každý endomorfismus je homomorfismus a každý automorfismus je izomorfismus, ale jména specificky zdůrazňují, že je uvažujeme jako zobrazení z jednoho prostoru do téhož prostoru. Složení endomorfismů jsou endomorfismy, navíc je lze mocnit:
fk = f ∘ f ∘ ⋯ ∘ f.
Endomorfismy jsou reprezentované
čtvercovými maticemi a typicky se volí pouze jedna báze, tedy
X=Y. Výhody takových reprezentací jsou, že iterování homomorfismu odpovídá mocninám reprezentující matice:
Pokud f je reprezentováno A, je fk reprezentováno Ak.
Izomorfismy jsou reprezentované
regulárními maticemi. Pokud existuje izomorfismus f : U ⟶ V, mají prostory U a V stejnou algebraickou strukturu vektorových operací + a *. Protože f je bijekce, můžeme
vektory U spárovat s vektory V, a operace se na nich aplikují identicky. Neznamená to, že by tyto prostory byly totožné matematické objekty, akorát jejich
algebraická struktura je totožná a v řadě případů můžeme
pracovat v U stejně jako ve V.
Tagy: #klicove
Iterační metody
Obecně existují v matematice dva druhy výpočetních metod. Přímé metody (například Gaussova eliminace) provádějí dlouhou sekvenci kroků, na jejichž koncí získáme řešení. Oproti tomu iterační metody postupují v kratších krocích a konstruují lepší a lepší aproximaci řešení.
V případě soustavy Ax=b počítají iterační metody posloupnost přibližných řešení x0,...,xk. Skončíme v k-tém kroku, když je chyba ek=x-xk dostatečně malá. Protože typicky vektor chyby ek neznáme, testujeme dostatečně malou velikost residua
rk = Aek = A(x-xk) = b - Axk.
Jeden ze zásadních rozdílů je, že pokud iterační metodu zastavíme v půlce, získáme alespoň nějaký odhad řešení, narozdíl od přímé metody. (Co víme o řešení soustavy, pokud Gaussova eliminace spočítá pouze polovinu odstupňovaného tvaru?)
Štěpící metody. Předpokládejme, že A = S - T a že pro matici S umíme snadno vyřešit soustavu (řekněme, že známe S-1). Potom Ax=b vede na Sx=Tx+b, neboli x=S-1Tx+S-1b. Tento vzorec můžeme použít k iterování:
xk+1 = S-1Txk+S-1b. Metoda konverguje pouze pro určité volby matic S a T, a velice pomalu. Typická volba S je diagonální část A nebo horní trojúhelníková část A. Jiný pohled na metody je, že S je aproximace matice A.
Metoda konjugovaných gradientů CG. Konstruuje postupně aproximace výpočtem Krylovova podprostoru
Kk = ⟨b, Ab, A2b, ..., Ak-1b⟩.
Volíme
xk∊K
k tak, aby minimalizovalo chybu řešení přes všechny vektory K
k, což lze udělat velice efektivně. Pro rozšíření Krylovova podprostoru je potřeba vynásobit vektor maticí, což vyžaduje n
2 operací. Protože typicky stačí udělat n
1/2 iterací, je metoda typicky rychlejší než Gaussova eliminace: n
5/2 operací.
Úpravy
Z rovnic lze vyvozovat nové informace jejich kombinováním. Budeme uvažovat dvě elementární operace a jejich kombinace:
- Násobení reálným číslem: z A=B získáme αA=αB.
- Součet dvou rovnic: z A=B a C=D získáme A+C=B+D.
Protože nechceme, aby počet rovnic rostl, vždy odvozenou rovnicí nahradíme nějakou předchozí, čímž získáme upravenou soustavu.
Výše uvedené úpravy nazýváme elementární úpravy.
Dále uvažujeme odvozené elementární úpravy:
- Přičtení 𝛼-násobku jedné rovnice k druhé.
- Prohození dvou rovnic.
Pokud nějaká n-tice (x1,...,xn) řeší soustavu, bude řešit i upravenou soustavu. Avšak obrácená implikace nemusí platit, množina řešení se může úpravou zvětšit.
Úprava se nazývá regulární (nebo ekvivalentní), pokud nemění množinu řešení obecně libovolné soustavy.
Tvrzení: Úpravy vynásobení nenulovým reálným číslem, přičtení jedné rovnice k druhé a jejich kombinace jsou regulární.
Důkaz: Výše uvedené úpravy lze invertovat, tedy existují úpravy, které převedou upravenou soustavu zpět do původního tvaru. Protože se množina řešení může pouze zvětšovat, nemohla se změnit.
 Tagy:
Tagy: #klicove
Hodnost transpozice
Následující věta je jedním z divů lineární algebry. Říká, že pro libovolnou matici A je dim Im(A) = dim R(A), přestože se jedná o zcela jiné prostory.
Věta: Pro libovolnou matici A platí, že rank(A) = rank(AT).
Maticové inverze
Mějme matici A velikosti m x n. Pokud existuje matice A-1 velikosti n x m splňující AA-1 = Im, nazývá se A-1 pravá inverze A. Nemusí být určena jednoznačně. Podobně se definuje levá inverze A-1, která splňuje A-1A = In.
Označme u1,...,um sloupce pravé inverze A-1. Musí splňovat soustavy
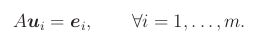
Lze nalézt
jednou Gaussovou eliminací s více pravými stranami:
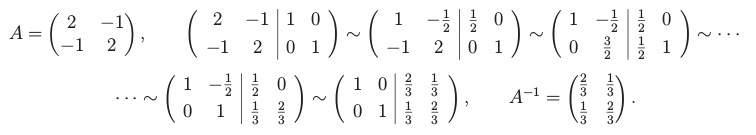 Uveďme několik tvrzení o existence inverzí, čtenář si může rozmyslet jejich důkazy:
Uveďme několik tvrzení o existence inverzí, čtenář si může rozmyslet jejich důkazy:
Tvrzení: Pro matici A existuje pravá inverze, právě když má soustava Ax=b řešení pro každou pravou stranu b. Neboli Im(A) je celý prostor ℝm.
Tvrzení: Nechť A je matice velikosti m x n. Pokud existuje pravá inverze, je m≤n. Pokud existuje levá inverze, je m≥n. Tedy oboustranná inverze může existovat pouze pro čtvercové matice.
Tvrzení: Pro matici A existuje pravá inverze, právě když existuje levá inverze pro matici AT.
Tvrzení: Matice A velikosti m x n má pravou inverzi, právě když rank(A)=m, a levou, právě když rank(A)=n. (To vychází z netriviálního faktu, že rank(A) = rank(AT).)
Úprava inverzní maticí: Pokud má matice A levou inverzi, můžeme provést úpravu Ax=b na A-1Ax=A-1b, neboli x=A-1b. Nepoužívá se při výpočtech, protože spočítat inverzní matici je složitější než vyřešit soustavu; avšak hodí se v teorii.
Tagy: #klicove
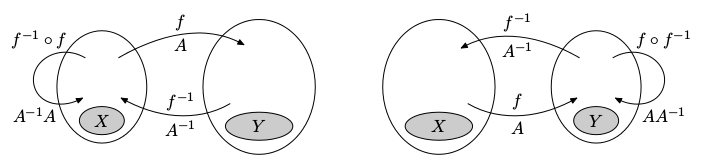
Inverzní zobrazení
Pro lineární zobrazení f : U ⟶ V může existovat inverzní zobrazení f-1 : V ⟶ U, nebo nemusí. Rozlišujeme tyto druhy inverzí:
- Levá inverze f-1 ∘ f = id existuje, právě když je zobrazení f prosté.
- Pravá inverze f ∘ f-1 = id existuje, právě když je zobrazení f na.
- Oboustranná inverze f-1 ∘ f = f ∘ f-1 = id existuje, právě když je zobrazení f bijektivní.
Protože identita je reprezentováná jednotkovou maticí In, je inverzní zobrazení reprezentováno inverzní maticí. Přesněji řečeno, nechť f je reprezentováno maticí A vůči bázím X a Y.
- Levá inverze f-1 je reprezentována levou inverzí A-1 vůči bázím Y a X (obrázek vlevo).
- Pravá inverze f-1 je reprezentována pravou inverzí A-1 vůči bázím Y a X (obrázek vpravo).
- Oboustranná inverze f-1 je reprezentována oboustrannou inverzí A-1 vůči bázím Y a X.
 Tagy:
Tagy: #klicove
LU dekompozice
Věta:
Pro libovolnou matici A velikosti m x n existuje dekompozice PA = LU, kde
- P je permutační matice m x m,
- L je dolní trojúhelníková matice m x m s jednotkovou diagonálou,
- U je horní trojúhelníková matice m x n.
Občas se uvažuje symetričtější varianta dekompozice PA=LDU, kde obě trojúhelníkové matice L a U mají jednotkové diagonály a D je diagonální matice pivotů.
Příklad: Nechť A je následující matice:
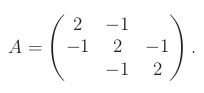
Získáváme následující LU a LDU dekompozice pro P=I
3:
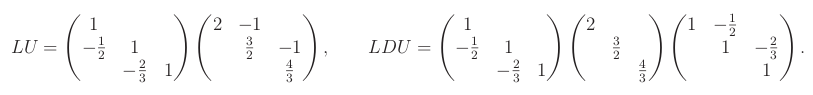 LU dekompozice je maticový zápis Gaussovy eliminace aplikované na A. Význam jednotlivých matic v dekompozici je následující:
LU dekompozice je maticový zápis Gaussovy eliminace aplikované na A. Význam jednotlivých matic v dekompozici je následující:
- Permutační matice P popisuje proházení řádků A tak, aby bylo možné provést Gaussovu eliminace PA bez pivotace.
- Matice L popisuje elementární úpravy dopředné eliminace. Protože jsme proházeli řádky pomocí P, stačí využívat pouze elementární úpravy přičtení 𝛼-násobku i-tého řádku k j-tému, kde i < j.
- Matice U je výsledný odstupňovaný tvar A, spolu s hodnotami pivotů.
Nechť jsou R1, ..., Rk matice techto elementárních úprav, které převedou PA v U. Platí maticová rovnost
RkRk-1⋯R2R1PA = U.
Matice úprav R
i jsou
dolní trojúhelníkové matice s jednotkovou diagonálou. Proto je L = (R
kR
k-1⋯R
2R
1)
-1 také dolní trojúhelníková matice s jednotkovou diagonálou. Získáváme dekompozici PA=LU.
Poznámka: Pokud je matice A
symetrická a lze ji eliminovat bez prohazování řádků, má její LDU dekompozice speciální
symetrickou formu A = LDLT.
Tagy: #klicove
Duální zobrazení
K lineárnímu zobrazení f : U ⟶ V je přiřazeno duální zobrazení f* : V ⟶ U, které má speciální vlastnosti. Povšimněme si, že inverzní zobrazeni f-1 : V ⟶ U zobrazuje mezi stejnými prostory (pokud existuje), avšak duální zobrazení je něco zcela jiného (například vždy existuje).
Definice přes skalární součin: Duální zobrazení f* : V ⟶ U je jediné zobrazení, které pro libovolné vektory x∊U a y∊V splňuje:
⟨f(x) | y⟩ = ⟨x | f*(y)⟩.
Povšimněme si, že levá strana rovnosti je skalární součin ve V, zatímco pravá v U.
Nechť A reprezentuje f vůči bázím X a Y.
Pro standardní skalární součin je f* reprezentováno AT. Tedy transpozice odpovídá dualitě.
Pro jaké báze reprezentuje AT zobrazení f*? Souřadnice bází X a Y můžeme popsat vůči kanonickým bázím maticemi přechodu X a Y (tedy jejich sloupcové vektory jsou souřadnice bazických vektorů).
Tvrzení: Pro standardní skalární součin je zobrazení f* jednoznačně určené a reprezentuje ho matice AT vůči duálním bázím Y* a X*, což jsou sloupcové vektory Y-T a X-T.
Důkaz: Dokažme to nejprve vůči kanonickým bázím. Nechť B je matice splňující ⟨Ax | y⟩ = ⟨x | By⟩. Zjevně pro B = AT to platí. Je to jediná taková matice, protože
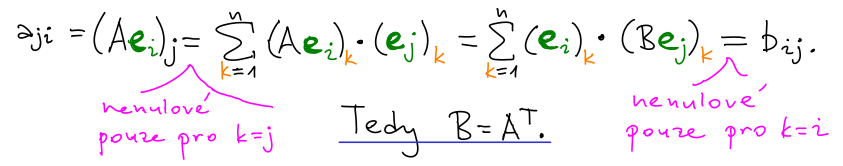
Pro obecné báze to platí z následujícího důvodu. Matice Y
-1AX reprezentuje f vůči kanonické bázi. Proto duální zobrazení f
* je reprezentováno (Y
-1AX)
T = X
TA
TY
-T vůči kanonické bázi.
Soustavy lineárních rovnic: Ax=b
Začneme příkladem soustava tří lineárních rovnic o třech neznámých:
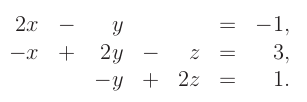
Hledáme
množinu všech řešení, což jsou trojice (x,y,z), které po dosazení splňují všechny tři rovnice současně. V tomto případě je
řešením jediná trojice (1,3,2).
Obecně soustava m lineárních rovnic o n neznámých:
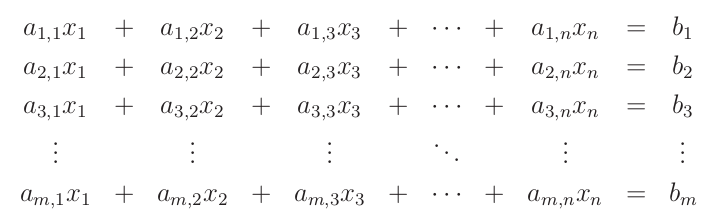
Čísla a
i,j a b
j jsou pevně zadaná a nazývají se
koeficienty. Čísla x
j se nazývají
neznámé a jejich hodnoty chceme nalézt.
Hledáme
množinu řešení tvořenou n-ticemi (x
1,...x
n) takovými, že po dosazení budou
zároveň splněny všechny rovnice.
Tagy: #klicove
Hodnost matice
Hodnost matice A se značí rank(A) a udává, jak moc je matice A blízká regulární matici. Několik ekvivalentních definic rank(A):
- dim Im(A), což je počet lineárně nezávislých sloupců matice a také dimenze obrazu příslušného lineárního zobrazení.
- dim R(A), neboli počet lineárně nezávislých řádků matice.
- počet nenulových řádků a počet pivotů v odstupňovaném tvaru A.
- nejmenší počet matic hodnosti jedna, jejichž součet je A.
Pro hodnost platí následující horní odhady:
- rank(A) ≤ min {m,n} pro matici A velikosti m x n.
- rank(A+B) ≤ rank(A) + rank(B).
- rank(AB) ≤ min {rank(A), rank(B)}.
Poslední nerovnost má následující důkaz v řeči lineárních zobrazení:
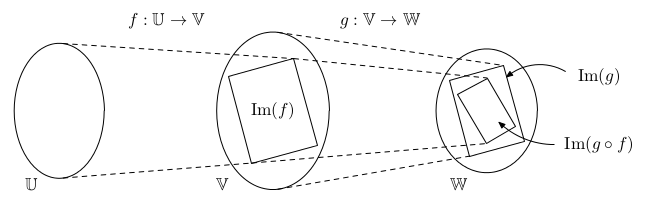 Tvrzení:
Tvrzení: Násobení regulární maticí zleva/zprava
nemění hodnost.
Důkaz: Dokažme pro násobení zleva. Podle nerovnosti je rank(RA) ≤ rank(A). Na druhou stranu, protože R je regulární,
A = R-1RA. Tedy rank(A) = rank(R
-1RA) ≤ rank(RA).
Permutační matice
Nechť 𝜋 je permutace množiny {1,...,n}. Je reprezentována permutační maticí P. To je čtvercová matice n x n, jejíž koeficienty jsou nuly a jedničky, a
(P)i,j = 1, právě když 𝜋(i)=j.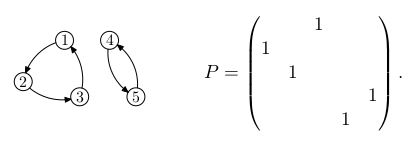
Nechť A je libovolná matice, kterou násobíme permutační maticí P.
- Násobení zprava permutuje řádky A podle 𝜋.
- Násobení zleva permutuje sloupce A podle 𝜋-1.
Nechť P𝜋 značí permutační matici reprezentující 𝜋. Čtenář si může rozmyslet a dokázat následující vlastnosti.
Součin permutačních je permutační matice, která reprezentuje složení příslušných permutací.
Tedy
P𝜋P𝜎 = P𝜋∘𝜎.
Každá permutační matice P je
regulární, dokonce
ortogonální, tedy existuje
inverzní matice, která je také permutační. Pro ni platí, že
P𝜋-1 = P𝜋-1 = P𝜋T.
Snadné je přímo z definice ověřit, že tato inverze je oboustranná.
Permutační matice tvoří
grupu. Podle Cayleyho věty je možné libovolnou grupu o n prvcích reprezentovat jako
grupu permutací {1,...,n}. Proto je možné libovolnou grupu o n prvcích reprezentovat
permutačními maticemi n x n. To přirozeně vede ke zkoumání pojmu maticových grup.
Trojúhelníkové matice
Rozlišujeme dva druhy trojúhelníkových matic. Typicky se uvažují čtvercové matice, ale definice funguje i pro obdélníkové.
Dolní trojúhelníková matice L má všechny koeficienty nad hlavní diagonálou nulové. Tedy (L)i,j = 0 pro i > j.
Horní trojúhelníková matice U má všechny koeficienty pod hlavní diagonálou nulové. Tedy (U)i,j = 0 pro i < j.
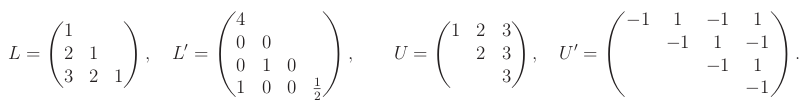
Diagonální matice jsou současně dolní a horní trojúhelníkové.
Nechť horní trojúhelníková matice U reprezentuje zobrazení vůči jedné bázi b1,...,bn. Protože Ubi leží v ⟨b1,...,bi⟩ (a podobně pro dolní trojúhelníkové matice L), je celá řada problému s trojúhelníkovými maticemi výrazně jednodušších. Například soustavy Lx = b a Ux = b lze řešit přímo substitucí. Je také jednoduché najít inverzní matice a určit vlastní čísla (prvky na diagonále).
Čtenář si může rozmyslet následující vlastnosti:
- Trojúhelníkové matice jsou uzavřené na součin. Tedy součin dolních trojúhelníkových matic je dolní trojúhelníková matice a podobně pro horní trojúhelníkové matice.
- Trojúhelníková matice je regulární právě tehdy, když jsou koeficienty na diagonále nenulové.
- Trojúhelníkové matice jsou uzavřené na inverze. Tedy inverzí dolní trojúhelníkové matice je dolní trojúhelníková matice, inverzí horní trojúhelníkové je horní trojúhelníková.
- Přímo z definice si můzeme rozmyslet, že čtvercová trojúhelníková matice má inverzi z jedné strany, právě když ji má z druhé strany. To je důležité pro důkaz obecné věty o oboustranné inverzi pomocí LU dekompozice.
Transpozice
Nechť A je matice m x n. Její transpozice AT je matice n x m s následujícími koeficienty:
(AT)i,j = (A)j,i.
Tedy koeficienty matice AT vzniknou zrcadlením koeficientů A podle hlavní diagonály.
Pro matice s komplexními čísly se transpozice definuje jinak. Značí se AH a čísla jsou navíc komplexně sdružená (což odpovídá jinému skalárnímu součinu). Transpozice se často také značí A* (jak reálná, tak komplexní).
Pro transponované matice platí následující vztahy, rozmyslete si jejich důkazy z definice maticových operací:
- (AT)T = A.
- (cA)T = cAT.
- (A+B)T = AT+BT.
- (AB)T = BTAT. Povšimněme si, že pořadí transponovaných matic musí být obrácené, aby měl součin kompatibilní rozměry. Jak vypadá transpozice obecně pro součin více matic?
- Pokud je A regulární matice, pak (A-1)T = (AT)-1 = A-T.
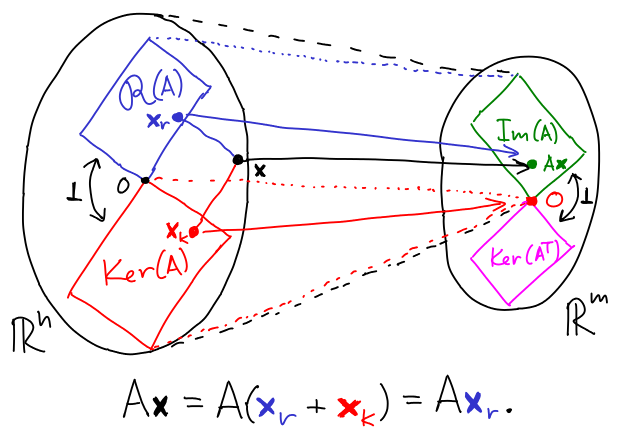
Fundamentální podprostory
Nechť A je matice m x n s řádkovými vektory r1, ..., rm a sloupcovými vektory s1, ..., sn. Matice A definuje čtyři fundamentální podprostory:
- Jádro Ker(A) = {x : Ax = 0} (neboli kernel).
- Řádkový prostor R(A) = Im(AT) = ⟨r1, ..., rm⟩ = {ATx : x∊ℝm} (neboli levý obraz).
- Levé jádro Ker(AT) = {y : yTA = 0} (neboli levý kernel).
- Sloupcový prostor S(A) = Im(A) = ⟨s1, ..., sn⟩ = {Ax : x∊ℝm} (neboli obraz).
Povšimněme si, že jádro a řádkový prostor jsou podprostory ℝn, zatímco levé jádro a sloupcový prostor jsou podprostory ℝm.
Fundamentální věta lineární algebry:
- Nechť r = rank(A). Platí, že
dim R(A) = dim Im(A) = r, dim Ker(A) = n-r a dim Ker(AT) = m-r. - R(A) a Ker(A) jsou lineárně nezávislé a generují ℝn. Podobně Im(A) a Ker(AT) jsou lineárně nezávislé a generují ℝm.
- Navíc jsou R(A) a Ker(A) ortogonální doplňky, tedy každý vektor z R(A) je kolmý na každý vektor z Ker(A). Podobně pro Im(A) a Ker(AT).
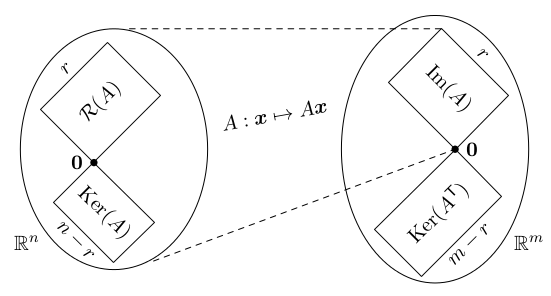
Poznamenejme, že vlastnost 1 platí nad obecným algebraickým tělesem. Vlastnosti 2 a 3 vyžadují ℝ (a při drobné změně definic fungují i nad ℂ).
Tagy: #klicove
Determinant
Blokové matice
Blokové matice jsou tvořené menšími maticemi, které se nazývají bloky. Můžeme definovat operace na blokových maticích kompatibilního typu. To umožňuje využívat blokový jazyk k efektivnímu popisu některých věcí.
Nechť A a B jsou dvě blokové matice velikosti 2n x 2n, tvořené čtyřmi bloky velikosti n x n.
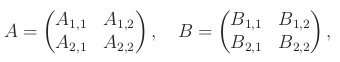
Tyto matice lze
sčítat po blocích a násobit po blocích:
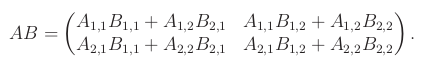
Čtenář si může rozmyslet, za jakých podmínek lze definovat operace obecně. Také lze definovat
blokově diagonální matice,
blokově trojúhelníkové matice, atd.
Blokové násobení se prakticky využívá při násobení velkých matic. Pro ně je potřeba číst koeficienty z paměti (řekněme RAM), která je mnohem pomalejší než rychlost výpočtů počítače. Řekněme, že násobíme matice velikosti n x n a do paměti dokážeme naráz načíst zhruba 2b2 koeficientů.
Pokud budeme postupovat podle definice, tak vždy určíme jeden koeficient AB vynásobením koeficientů řádku A a sloupce B. Na to potřebujeme udělat n/b2 čtení z paměti, tedy celkem n3/b2 součinů.
Místo toho rozdělíme obě matice na bloky b x b (pro jednoduchost nechť n je násobek b). Pro výpočet hodnot jednoho bloku AB musíme vynásobit jeden řádek bloků A s jeden sloupcem bloků B. Na to potřebujeme udělat n/b čtení. Bloků AB je n2/b2, tedy dohromady děláme n3/b3 čtení, což je b-krát efektivnější.
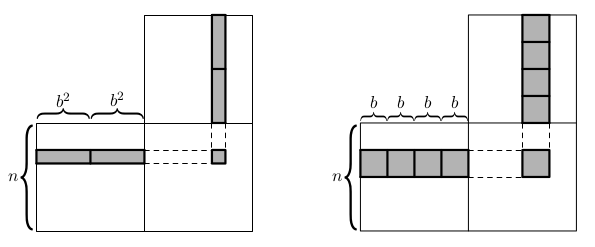
Hodnost 1
Matice A má hodnost 1, pokud je nenulová a každý její řádek/sloupec je násobek ostatních. Existuje elegantní zápis
A = xyT,
kde x a y jsou nenulové vektory.
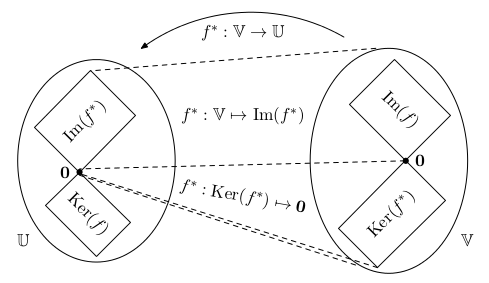
Fundamentální podprostory
Lineární zobrazení f : U ⟶ V definuje dva fundamentální podprostory:
- Jádro Ker(f) = {x : f(x) = 0} (neboli kernel).
- Obraz Im(f) = {f(x) : x∊U}.
Jádro je podprostor U, zatímco obraz je podprostor V. Pokud matice A reprezentuje f, tyto podprostory odpovídají Ker(A) a Im(A).
Čemu však odpovídají zbývající dva fundamentální podprostory A? Jsou to jádro a obraz duálního zobrazení f* : V ⟶ U.
- Levé jádro Ker(f*) = {x : f*(x) = 0} (neboli levý kernel).
- Levý obraz Im(f*) = {f*(x) : x∊U}.
Na obrázku je naznačeno duální zobrazení spolu se svými fundamentálními podprostory.
Speciální matice
Některé druhy matic se objevují v lineární algebře často, že se pro ně vyplatí mít speciální jména.
Jsou zajímavé ze dvou důvodu:
- Vyskytují se často v lineární algebře a v různých aplikacích.
- Mají speciální vlastnosti, kterých lze využít například při výpočtech či strukturální analýze.
Diagonální matice
Diagonální matice D má všechny koeficienty mimo hlavní diagonálu nulové, tedy (D)i,j = 0 pro i ≠ j. Definice funguje i pro obdelníkové matice.
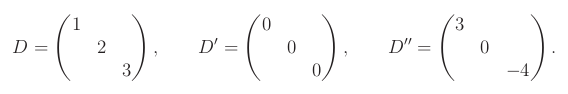 Jednotková matice
Jednotková matice I
n je diagonální matice n x n s jedničkami na diagonále.
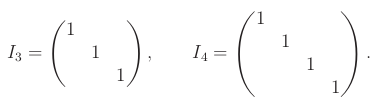 Pokud reprezentují endomorfismus vůči jedné bázi, odpovídají natažení souřadních os. V případě jednotkové matice se jedná o identitu.
Pokud reprezentují endomorfismus vůči jedné bázi, odpovídají natažení souřadních os. V případě jednotkové matice se jedná o identitu.
Tvrzení: Libovolné lineární zobrazení f je reprezentováno vůči vhodným bázím X a Y diagonální maticí, která má na diagonále pouze 1 a 0.
Důkaz: Nechť Xr je libovolná báze levého obrazu Im(f*) a Xk je libovolná báze jádra Ker(f). Zvolíme X = Xr ∪ Xk.
Protože f definuje izomorfismus mezi Im(f*) a Im(f), zobrazuje libovolnou bázi Im(f*) na bázi Im(f). Tedy f(Xr) je báze Im(f), kterou doplníme bází Ker(f*) a získáme druhou hledanou bázi Y. Protože f(Xk) = {0}, je zobrazení f reprezentováno vůči X a Y popsanou diagonální matici.
Tvrzení: Čtvercová matice A komutuje s každou čtvercovou maticí, právě když A=cIn.
Pozitivně definitní matice
Čtvercová symetrická matice A se nazývá pozitivně definitní, právě když platí jedna z následujících šesti ekvivalentních vlastností:
- Pro každé x ≠ 0 je xTAx > 0.
- Všechna vlastní čísla 𝜆i > 0. (Vlastní čísla jsou reálná ze symetrie A.)
- Determinanty principiálních minorů det(A1), ..., det(An) > 0. Principiální minor Ak je čtvercová podmatice A velikosti k x k v levém rohu.
- Lze provést Gaussovu eliminaci bez prohazování a násobení řádků a všechny pivoty pi > 0.
- Existuje regulární matice R taková, že A = RTR, což je Choleského rozklad.
- Výraz xTAy je skalární součin a √xTAy je norma.
Tvrzení: Pro symetrické matice A jsou vlastnosti 1 až 6 ekvivalentní.
Skalární součin
Skalární součin lze definovat konkrétně formulí nebo abstraktně pomocí vlastností.
Standardní skalární součin je definován výrazem
⟨x | y⟩ = xTy = ∑ xiyi = x1y1 + ⋯ + xnyn.
Abstaktní definice popisuje skalární součin jako libovolné zobrazení ℝ
n ⨯ ℝ
n ⟶ ℝ splňující vlastnosti:
- Linearita: ∀ x, y, z ∊ ℝn: ⟨x+y | z⟩ = ⟨x | z⟩ + ⟨y | z⟩.
∀ x, y ∊ ℝn, 𝛼 ∊ ℝ: ⟨𝛼*x | y⟩ = 𝛼*⟨x | y⟩. - Symetrie: ∀ x, y ∊ ℝn: ⟨x | y⟩ = ⟨y | x⟩.
- Pozitivní definitnost: ∀ x ∊ ℝn, x ≠ 0: ⟨x | x⟩ > 0.
(Poznámka: Pro x = 0 je ⟨x | x⟩ = 0 z linearity.)
Libovolné zobrazení splňující první vlastnost (v obou složkách) se nazýva
bilineární forma, dvojicím vektorů přiřazuje reálná čísla a je lineární v obou složkách. Tedy skalární součin je
symetrická pozitivně definitní bilineární forma. Rozmyslete si, že standardní skalární součin vlastnosti 1 až 3 splňuje.
Nad tělesem komplexních čísel ℂ se komplexně sdružuje: Standardní skalární součin má komplexně sdružené koeficienty
x. Abstraktní skalární součin má ve vlastnosti 2 komplexní sdružení.
Skalární součin (třeba standardní) je možné definovat stejně i nad obecnými algebraickými tělesy, ale
pozitivní definitnost nemůže být splněna (nad obecným tělesem dokonce nerovnost nedává smysl). Tedy skalární součin je výrazně slabší pojem nad obecnými tělesy.
Výraz xTy lze přirozeným způsobem zobecnit na xTAy, kde A je nějaká matice.
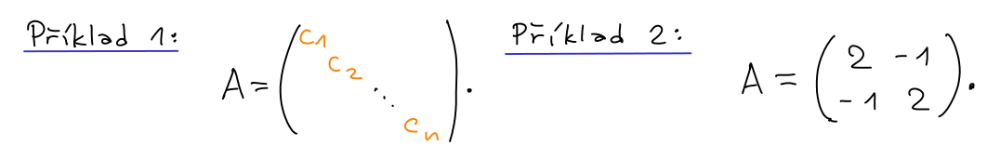
V příkladu 1 je potřeba kvůli třetí vlastnosti, aby každé c
i bylo kladné. V příkladu 2 lze vlastnost 3 dokázat převodem na součet čtverců:
⟨x | x⟩ = 2x12 - 2x1x2 + 2x22 = x12 + x22 + (x1 - x2)2 > 0.
Výraz
xTA
y je obecně bilineární forma.
- Pokud je matice A symetrická, je to symetrická bilineární forma.
- Pokud je A navíc pozitivně definitní (∀ x ≠ 0: xTAx > 0), je to symetrická pozitivně definitní bilineární forma, neboli skalární součin.
Věta: Libovolný skalární součin ⟨
x |
y⟩ je roven
xTA
y, kde A je nějaká
symetrická pozitivně definitní matice.
Důkaz: Nechť
e1, ...,
en je kanonická báze. Z linearity je skalární součin jednoznačně určený hodnotami pro libovolnou bázi:
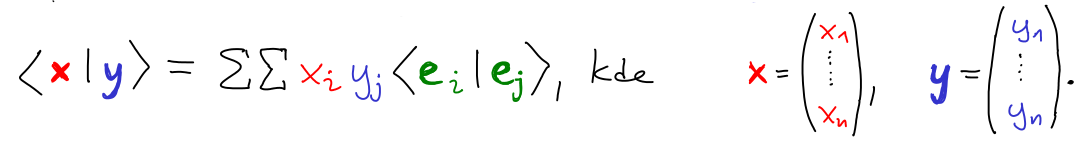
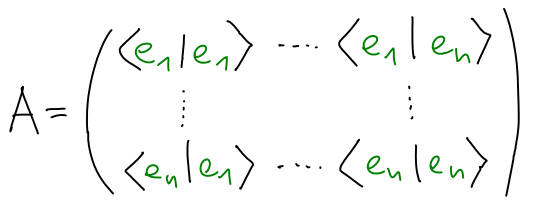
Jako A zvolíme
Gramovu matici tvořenou skalárními součiny ⟨
ei |
ej⟩. Potom je ⟨
x |
y⟩ =
xTA
y. Z vlastností 2 a 3 skalárního součinu vyplývá, že A je symetrická pozitivně definitní matice.
Kvadratické formy a definitnost
Ortogonální matice
Matice Q se nazývá ortogonální, pokud má ortonormální sloupce (ortogonalita + normy rovné jedné). V maticovém zápisu dostáváme QTQ = In.
Tedy pro ortogonální matice platí, že Q-1 = QT. Protože inverze libovolné čtvercové matice je oboustranná, dostáváme navíc, že QQT = In. Tedy pokud má čtvercová matice ortonormální sloupce, má také ortonormální řádky, a také matice QT je ortogonální.
Skalární součin, norma a kolmost
Cíl je nad vektorovým prostorem ℝn zavést další geometrické pojmy.
- Skalární součin ⟨x | y⟩ dvou vektorů x a y popisuje, jak moc ukazují společným směrem a souvisí s úhlem, které vektory svírají.
- Kolmé vektory (neboli ortogonální vektory) nemají žádný společný směr, což je právě tehdy, když ⟨x | y⟩ = 0.
- Norma ∥x∥ je geometrická délka vektoru.
V matematice se často objevují prostory prvků (nemusí být vektorové prostory) obohacené nějakými geometrickými vlastnostmi. Dostáváme následující hierarchii možných geometrii:
skalární součin ⇒ norma ⇒ metrika ⇒ topologie.
Například prostor může být povrch koule, na kterém můžeme uvažovat geometrické vzdálenosti. Z těchto definic lze uvažovat topologii a metriku, ale nemůžeme definovat skalární součin a normu.
- Prostor se skalárním součinem. Nad prostorem lze uvažovat úhly a kolmost. Existence skalárního součinu indukuje normu: ∥x∥ = √⟨x | x⟩.
- Prostor s normou. Nad prostorem lze uvažovat vzdálenosti, které se chovají lineárně vůči natahování vektorů: ∥c*x∥ = |c|*∥x∥. Norma indukuje metriku 𝜌(x,y) = ∥x-y∥.
- Prostor s metrikou. Metrika je funkce vzdálenosti 𝜌(x,y), která je nezáporná (a kladná pro x ≠ y), symetrická a splňuje trojúhelníkovou nerovnost. Oproti normě nemusí mít prostor strukturu vektorového prostoru, tedy nemusí platit linearita. Norma indukuje topologii pomocí otevřených a uzavřených 𝜀-okolí, což jsou množiny B𝜀(x) = {y : 𝜌(x,y) ≤ 𝜀} (případně s ostrou nerovností).
- Prostor s topologií. Nemáme přímo definovanou vzdálenost, ale topologie popisuje blízkost. To se dělá pomocí systému uzavřených a otevřených okolí. Výhoda je, že v řadě situací vzdálenost vůbec nepotřebujeme. Nad topologickými prostory lze dělat velkou část analýzy. Například můžeme definovat limitu posloupnosti: lim xn = x, pokud pro každé otevřené okolí bodu x existuje N > 0 takové, že pro n > N leží každé xn v tomto okolí x.
Symetrické matice
Čtvercová matice A se nazývá symetrická, pokud platí A=AT. Symetrické matice reprezentují endomorfismy, které jsou sami sobě duální.
Symetrické matice řadu speciálních vlastností, například jsou uzavřené na součiny a inverze.
Ortonormální báze
Z lineární nezávislosti ortogonálních vektorů má pojem ortogonální báze smysl. Typicky navíc máme ortonormální s jednotkovou normou: není to klíčové, ale zjednodušuje to vzorce.
Tvrzení: Libovolnou ortogonální/ortonormální množinu nenulových vektorů lze rozšířit na ortogonální/ortonormální bázi.
Důkaz:
Doplníme ortonormální množinu na libovolnou bázi a aplikujeme Gram-Schmidtovu ortogonalizaci. Alternativní důkaz je možný přes fundamentální větu lineární algebry.
Tedy ortogonálních bází je spousta a jsou to hezké báze, mající řadu skvělých vlastností.
1. Ortonormální báze mají výhodné numerické vlastnosti.
 2. Snadný výpočet souřadnic pomocí ortogonálních projekcí.
2. Snadný výpočet souřadnic pomocí ortogonálních projekcí. Pro obecnou bázi je to řešení soustavy lineárních rovnic A
𝛼 =
x. Pro ortogonální bázi
v1, ...,
vn je

Důkaz vyplývá z ortogonality: ⟨
x |
vi⟩ = ⟨
𝛼1v1 + ⋯ +
𝛼nvn |
vi⟩ =
𝛼i*⟨
vi |
vi⟩.
Jiný pohled je přes ortogonální matice:
𝛼 = Q
TQ
𝛼 = Q
Tx, pokud sloupce Q jsou ortonormální vektory
v1, ...,
vn.
Norma
Norma ∥x∥ je geometrická délka vektoru x. Opět má různé definice.
Norma indukovaná skalárním součinem. Libovolný skalární součin ⟨x | y⟩ definuje normu ∥x∥ = √⟨x | x⟩. Například standardní skalární součin definuje standardní normu
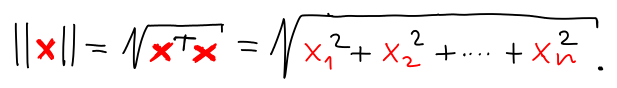
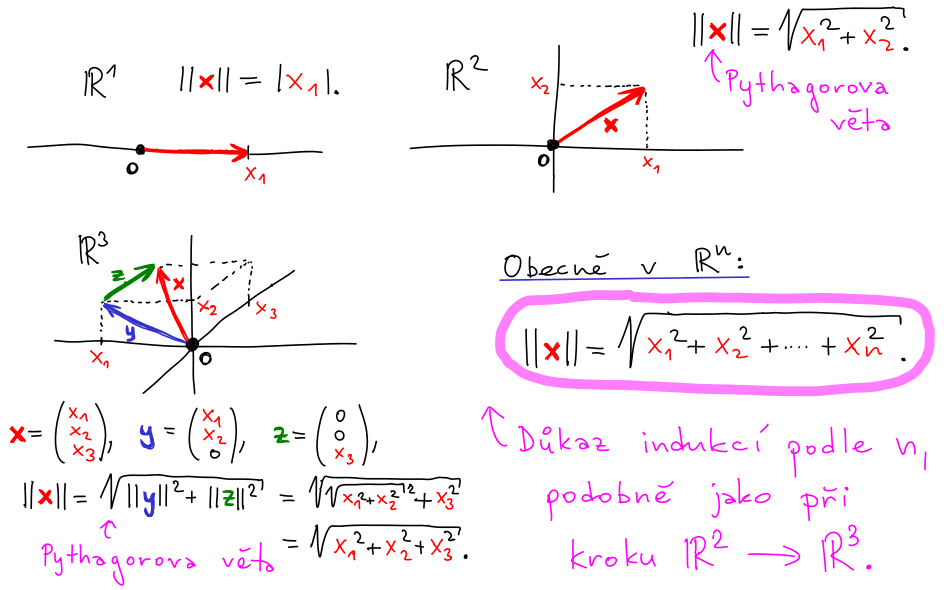
Vlastnosti 1 a 3 vyplývají z příslušných vlastností skalárního součinu. Pro trojúhelníkovou nerovnost:
 Abstaktní definice
Abstaktní definice popisuje normu jako libovolné zobrazení ℝ
n ⟶ ℝ splňující vlastnosti:
- Linearita: ∀ x ∊ ℝn, 𝛼 ∊ ℝ: ∥𝛼*x∥ = 𝛼|*∥x∥.
- Trojúhelníková nerovnost: ∀ x, y ∊ ℝn: ∥x+y∥ ≤ ∥x∥ + ∥y∥.
- Nezápornost: ∀ x ∊ ℝn, x ≠ 0: ∥x∥ > 0.
(Poznámka: Pro x = 0 je ∥x∥ = 0 z linearity.)
Ortogonální doplněk
Nechť U je libovolný vektorový podprostor. Ortogonální doplněk U je množina
U⊥ = {x : x ⊥ y pro každé y ∊ U}.
Tvrzení: Ortogonální doplněk
U⊥ má následující vlastnosti:
- U⊥ je vektorový podprostor.
- U ∩ U⊥ = {0} a ⟨U ∪ U⊥⟩ = ℝn.
- dim U + dim U⊥ = n.
- (U⊥)⊥ = U.
Důkaz: Vlastnosti 1 a první část 2 jsou jednoduché. Pro zbytek potřebujeme existenci ortogonálních bází. Zvolme ortogonální bázi
b1, ...,
bk prostoru U a doplňme ji vektory
bk+1, ...,
bn na ortogonální bázi ℝ
n. Vektory
bk+1, ...,
bn tvoří ortogonální bázi
U⊥. Pokud totiž nějaký vektor má nenulovou souřadnici vůči
b1, ...,
bk, nemůže ležet v
U⊥.
Fundamentální podprostory matice A jsou svoje ortogonální doplňky:
Ker(A) = R(A)⊥, Ker(AT) = Im(A)⊥.
Důkaz: Nechť
x ∊ Ker(A) a
u1, ...,
um jsou řádky matice A. Z definice je
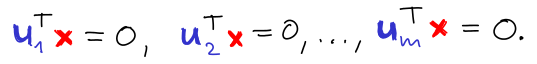
Tedy
x je ortogonální na R(A), a naopak libovolný ortogonální vektor na R(A) patří do Ker(A). Proto je Ker(A) = R(A)
⊥. Druhá rovnost se získá pro A
T.
Cauchy-Schwarzova nerovnost
Věta: (Cauchy-Schwarz) Pro libovolné vektory x a y platí nerovnost
|⟨x | y⟩| ≤ ∥x∥*∥y∥.
Poznámka: Věta má následující aplikaci ve
funkcionální analýze. Na prostoru funkcí můžeme definovat skalární součin a příslušnou indukovanou normu, například
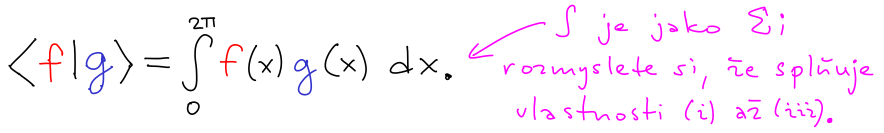
Protože se chceme vyhnout nekonečným hodnotám, můžeme uvažovat
Hilbertův podprostor všech funkcí, které mají konečnou normu. Podle Cauchy-Schwarzovy věty jsou i jejich skalární součiny konečné.
Cosinová věta: Pro libovolné vektory
x a
y svírající úhel 𝜑 platí, že
⟨x | y⟩ = ∥x∥*∥y∥*cos(𝜑).
Skalární součin je
kladný pro
ostrý úhel 𝜑,
nulový pro
kolmý úhel 𝜑 a
záporný pro
tupý úhel 𝜑.
Uvažme kolmou projekci p vektoru x na vektor y. Platí, že norma ∥e∥ rozdílu projekce a vektoru e = p - x je nezáporná. Úpravou získáváme Cauchy-Schwarzovu nerovnost:
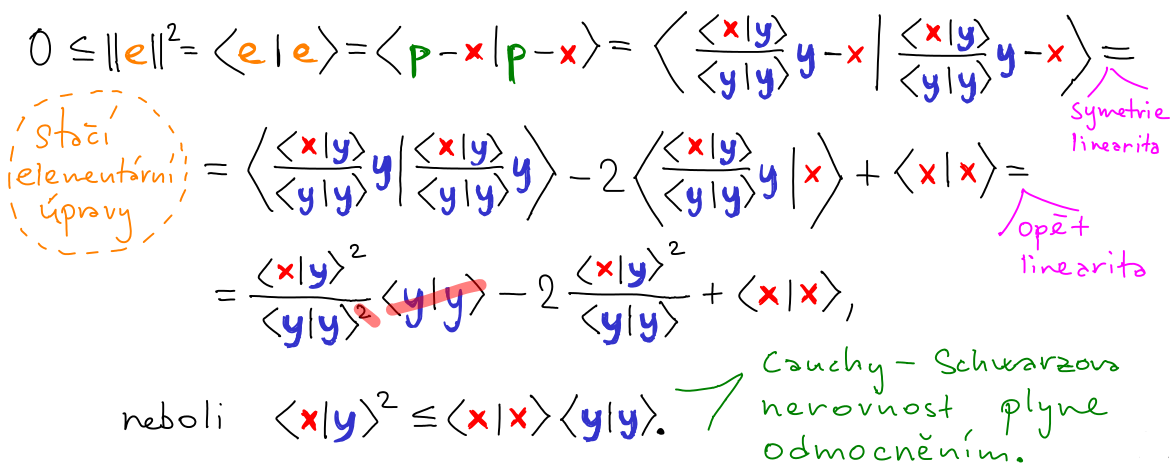
Charakterizace norem ℝ n
Podle charakterizace jsou normy indukované skalárním součinem tzv. A-normy ∥x∥A = √xTAx, kde A je symetrická pozitivně definitní matice. Norem však existuje mnohem víc než skalárních součinů.
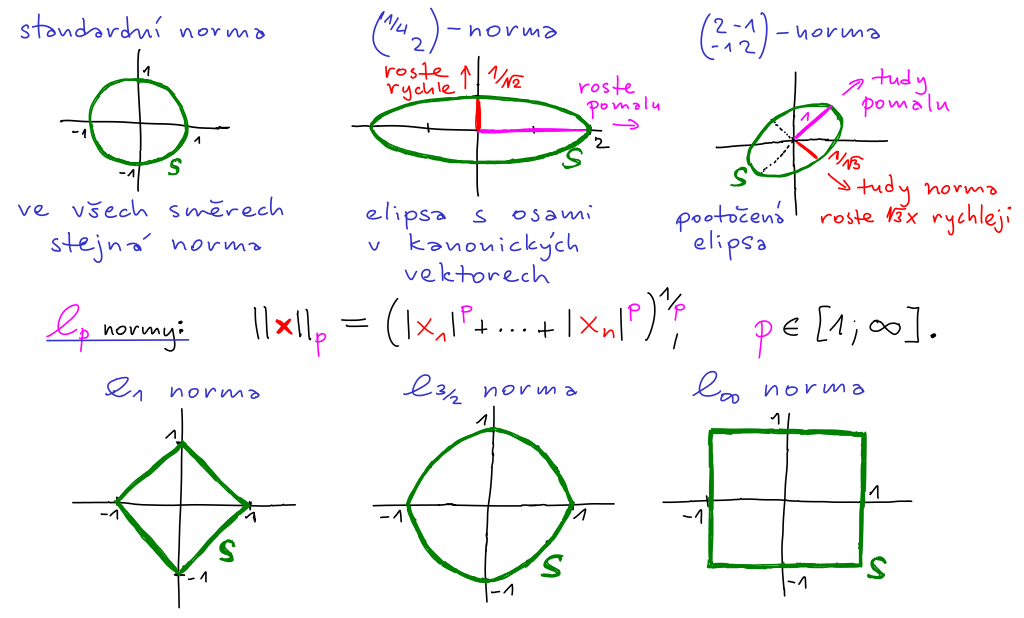 Uvažme pro danou normu jednotkovou sféru S a kouli B:
Uvažme pro danou normu jednotkovou sféru S a kouli B:
S = {x : ∥x∥ = 1}, B = {x : ∥x∥ ≤ 1}.
Geometrické vlastnosti sféry a koule.
Z axiomů normy můžeme vyvodit geometrické vlastnosti
S a
B.
- Množina S protíná každou přímku procházející počátkem přesně ve dvou bodech (podle linearity a nezápornosti).
- Množina S je symetrická podle počátku: S = -S (podle linearity se záporným koeficientem), a neobsahuje počátek: 0 ∉ S (podle nezápornosti).
- Množina B je konvexní (nejobtížnější, podle trojúhelníkové nerovnosti).
Klíčové je, že norma je
jednoznačně popsaná jednotkovou sférou S. Na libovolném paprsku z počátku má přesně jeden vektor
y jednotkovou normu. Norma zbývajících vektorů
x paprsku je určena z linearity.
 Tvrzení:
Tvrzení: Nechť
B je uzavřená omezená podmnožina ℝ
n, symetrická podle počátku. Nechť
S je hranice
B a
0 ∉
S. Potom je zobrazení ∥⋅∥ : ℝ
n ⟶ ℝ, kde
∥x∥ = |𝛼| pro x = 𝛼*y a y ∊ S,
norma.
Tvrzení: Pro normy indukované skalárním součinem je
jednotková sféra S pootočený elipsoid, jehož osy jsou vlastní vektory matice A.
Normální matice
Matice A se nazývá normální, pokud komutuje se svoji transpozicí: AA* = A*A. Normální matice jsou zobecněním symetrických matic.
Ortogonalita
Vektory x a y jsou ortogonální neboli kolmé, právě když ⟨x | y⟩ = 0. Kolmost značíme x ⊥ y.
Odvození přes Pythagorovu větu. Vektory x a y jsou kolmé, právě když splňují Pythagorovu větu.
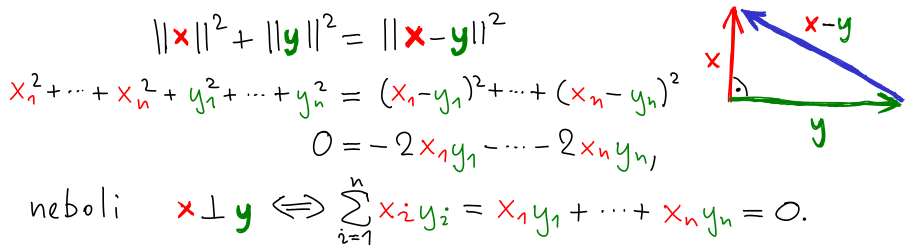
Podle definice je počátek
0 kolmý na všechny vektory.
Lemma: Nechť x1, ..., xn jsou nenulové po dvou ortogonální vektory, tedy xi ⊥ xj pro i ≠ j. Potom jsou vektory x1, ..., xn lineárně nezávislé.
Důkaz: Nechť 𝛼1*x1 + ⋯ + 𝛼n*xn = 0. Chceme dokázat, že všechna 𝛼i = 0. Vynásobíme-li celý výraz zleva xiT, dostáváme z ortogonality
0 = 𝛼1*xiTx1 + ⋯ + 𝛼i*xiTxi + ⋯ + 𝛼n*xiTxn = 𝛼i*xiTxi = 𝛼i*∥xi∥2.
Protože
xi ≠
0, víme, že
𝛼i = 0. Protože to platí při násobení libovolným
xiT, je lineární kombinace
𝛼1*
x1 + ⋯ +
𝛼n*
xn triviální.
Kolmost vektorových podprostorů.
QR dekompozice
Gram-Schmidtova ortogonalizace
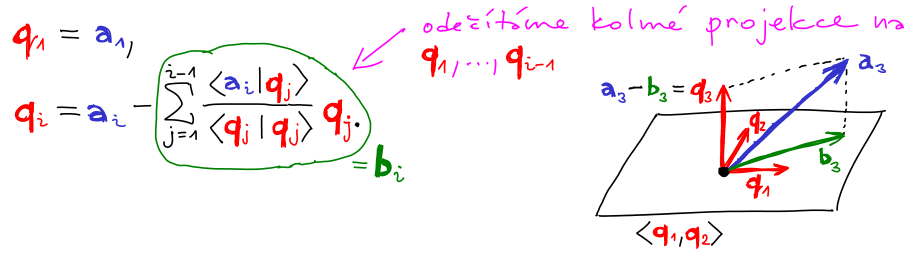
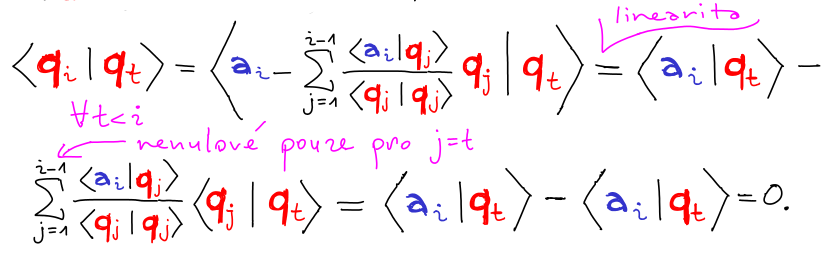
SVD
Vlastní čísla
Ortogonální projekce
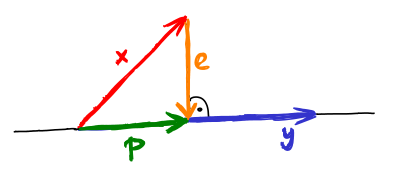 Mějme dva vektory x a y. Chceme nalézt kolmou projekci x na přímku ⟨y⟩. Ekvivalentně je kolmá projekce vektor přímky, který je nejbližší k x.
Mějme dva vektory x a y. Chceme nalézt kolmou projekci x na přímku ⟨y⟩. Ekvivalentně je kolmá projekce vektor přímky, který je nejbližší k x.
Víme, že p = c*y. Hledáme hodnotu c, aby vektor e = p - x byl kolmý na y:
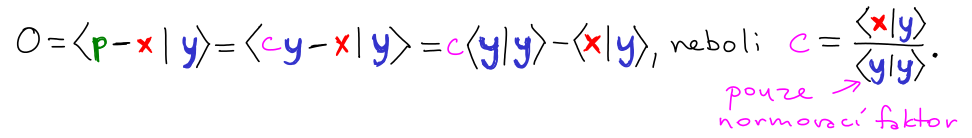 Tvrzení:
Tvrzení: Kolmá projekce na přímku ⟨
y⟩ je lineární zobrazení
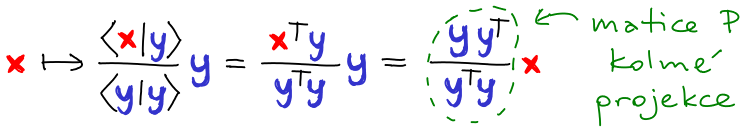 Nechť P je matice kolmé projekce na podprostor Im(P). Splňuje dvě následující podmínky:
Nechť P je matice kolmé projekce na podprostor Im(P). Splňuje dvě následující podmínky:
1. Charakteristika libovolné projekce: P2 = P.
Projekce je identita na Im(P), tedy Py = y pro libovolné y ∊ Im(P). Protože y = Px pro každé x, získáváme rovnost.
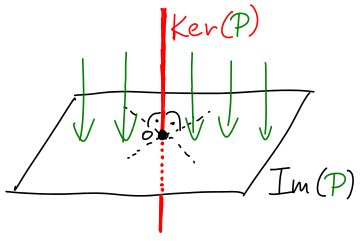 2. Charakteristika kolmosti projekce: PT = P. Ker(P) je tvořen vektory, které se projektují na 0, což jsou přesně vektory kolmé na Im(P). Tedy Ker(P) = Im(P)⊥ a z fundamentální věty lineární algebry je Ker(P) = Ker(PT) a R(P) = Im(P).
2. Charakteristika kolmosti projekce: PT = P. Ker(P) je tvořen vektory, které se projektují na 0, což jsou přesně vektory kolmé na Im(P). Tedy Ker(P) = Im(P)⊥ a z fundamentální věty lineární algebry je Ker(P) = Ker(PT) a R(P) = Im(P).
Zbytek plyne z duality, pokud ⟨Px | y⟩ = ⟨x | Py⟩. Zvolme
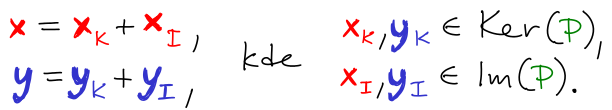
Protože
Px =
xI a
Py =
yI,
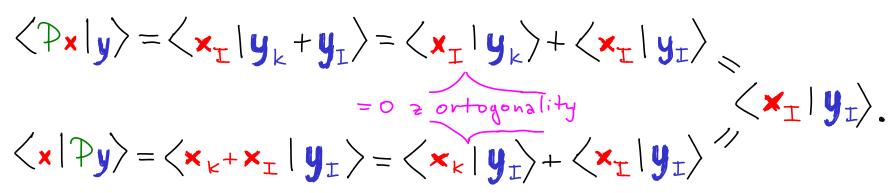 Tvrzení:
Tvrzení: Pokud sloupce matice A tvoří bázi podprostoru W, je kolmá projekce na W popsána maticí
P = A(ATA)-1AT.Fourierova transformace
Metoda nejmenších čtverců
 Cayley vymyslel v 1878 způsob, jak vizualizovat grupy pomocí diagramů. Vrcholy jsou jednotlivé prvky grupy 𝔾. Hrany popisují množinu generátorů g1, ..., gk, pro kterou
Cayley vymyslel v 1878 způsob, jak vizualizovat grupy pomocí diagramů. Vrcholy jsou jednotlivé prvky grupy 𝔾. Hrany popisují množinu generátorů g1, ..., gk, pro kterou
 Složitější konečná tělesa však existují i pro jiné velikosti, například GF(4) vpravo.
Složitější konečná tělesa však existují i pro jiné velikosti, například GF(4) vpravo.
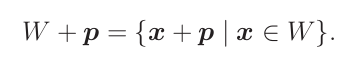

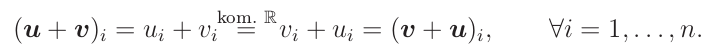
 Tento důkaz ilustruje obecný princip algebry. Matematické struktury jsou definovány tak, že jsou složeny z jednodušších struktur spolu s přidanými operacemi a vztahy. Pochopitelně tento řetěz někdy musí skončit, tedy nějakou základní strukturu musíme přímo popsat. Situace je podobná jako s ruskými panenkami Matrjoška.
Tento důkaz ilustruje obecný princip algebry. Matematické struktury jsou definovány tak, že jsou složeny z jednodušších struktur spolu s přidanými operacemi a vztahy. Pochopitelně tento řetěz někdy musí skončit, tedy nějakou základní strukturu musíme přímo popsat. Situace je podobná jako s ruskými panenkami Matrjoška.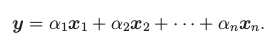
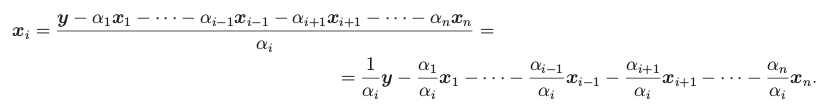






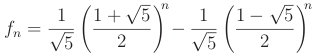
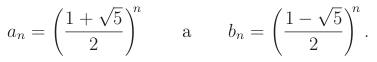
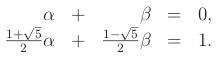


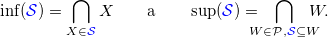

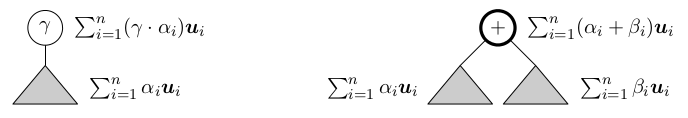
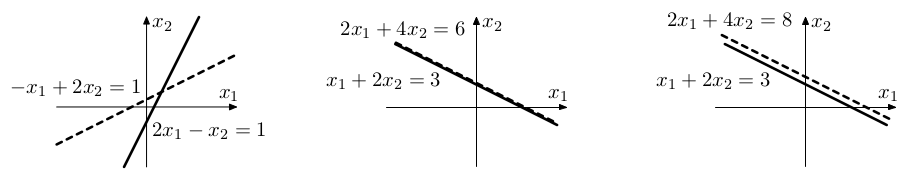 Vlevo je to jeden bod, ležící v průniku dvou přímek. Uprostřed je v průniku celá přímka. Vpravo je prázdný průnik, neboť jsou přímky rovnoběžné.
Jak vypadá množina Ri obecně?
Vlevo je to jeden bod, ležící v průniku dvou přímek. Uprostřed je v průniku celá přímka. Vpravo je prázdný průnik, neboť jsou přímky rovnoběžné.
Jak vypadá množina Ri obecně?


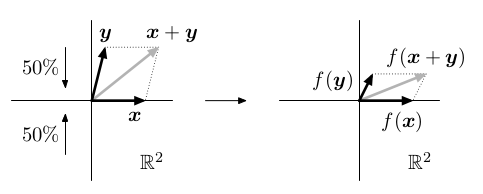


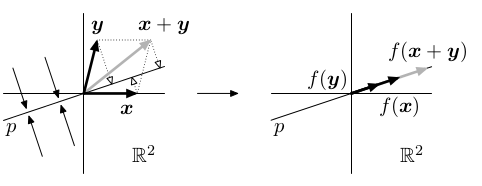
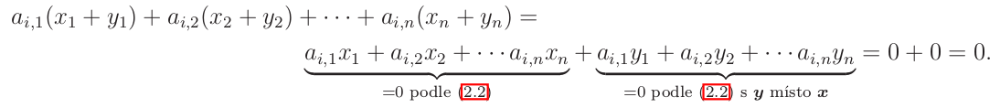
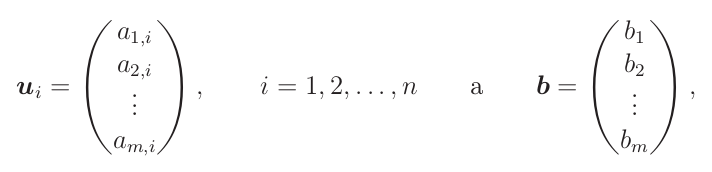
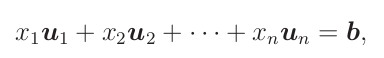
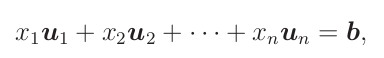
 Věta: Existuje právě jeden polynom P(x) stupně n, který prochází libovolnými n+1 body
Věta: Existuje právě jeden polynom P(x) stupně n, který prochází libovolnými n+1 body
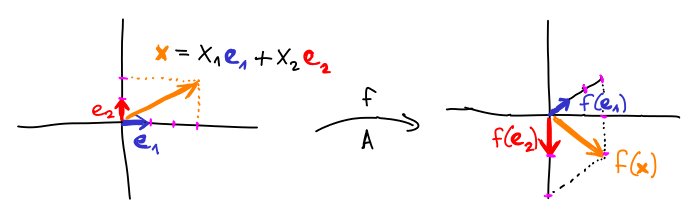

 Víme, že lineární zobrazení f : U ⟶ V je jednoznačně určeno obrazy libovolné báze. Zvolíme libovolně dvě báze:
Víme, že lineární zobrazení f : U ⟶ V je jednoznačně určeno obrazy libovolné báze. Zvolíme libovolně dvě báze:
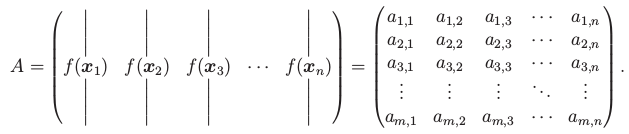
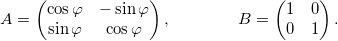 Například uvažme rotaci o úhel 𝜑 v rovině. Ta je reprezentovaná maticí A, pokud X=Y je kanonická báze tvořená vektory (1,0) a (0,1). Pokud však X je kanonická báze a Y je X otočená o úhel 𝜑, je rotace reprezentovaná maticí B. Na druhou stranu, pokud X=Y a zobrazení je endomorfismus, reprezentuje matice B identické zobrazení.
Například uvažme rotaci o úhel 𝜑 v rovině. Ta je reprezentovaná maticí A, pokud X=Y je kanonická báze tvořená vektory (1,0) a (0,1). Pokud však X je kanonická báze a Y je X otočená o úhel 𝜑, je rotace reprezentovaná maticí B. Na druhou stranu, pokud X=Y a zobrazení je endomorfismus, reprezentuje matice B identické zobrazení.
 Podle věty lze homomorfismus f : U ⟶ V rozdělit na složení dvou jednodušších homomorfismů:
Podle věty lze homomorfismus f : U ⟶ V rozdělit na složení dvou jednodušších homomorfismů:
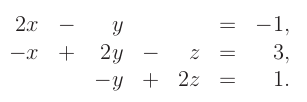
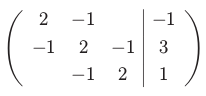
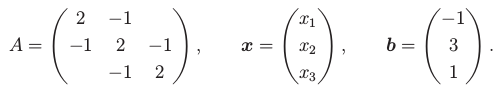




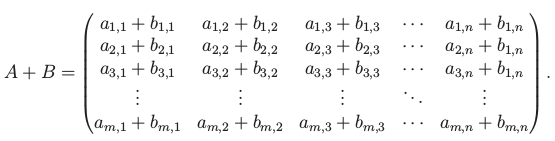


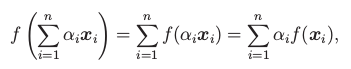


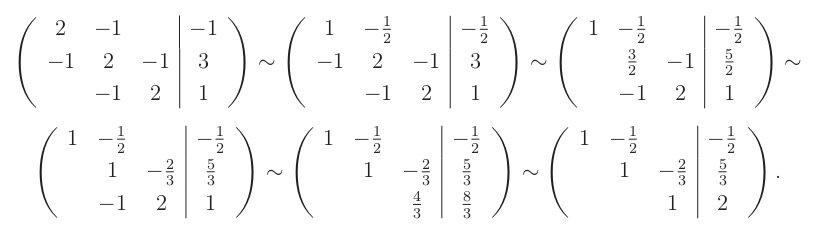
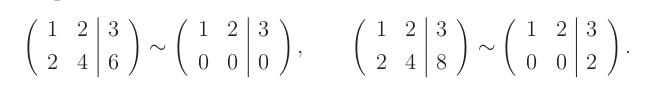






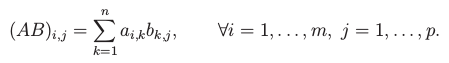


 Každý endomorfismus je homomorfismus a každý automorfismus je izomorfismus, ale jména specificky zdůrazňují, že je uvažujeme jako zobrazení z jednoho prostoru do téhož prostoru. Složení endomorfismů jsou endomorfismy, navíc je lze mocnit:
Každý endomorfismus je homomorfismus a každý automorfismus je izomorfismus, ale jména specificky zdůrazňují, že je uvažujeme jako zobrazení z jednoho prostoru do téhož prostoru. Složení endomorfismů jsou endomorfismy, navíc je lze mocnit:
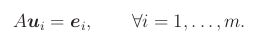
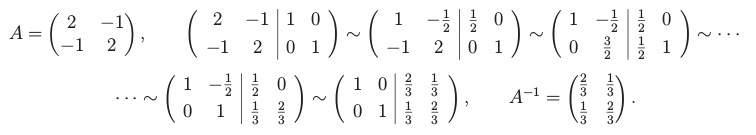

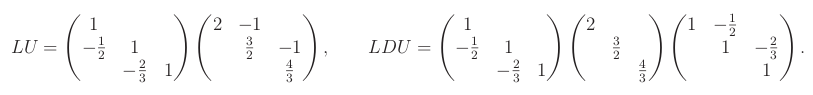
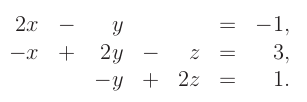
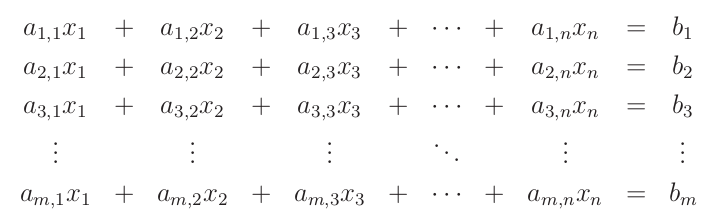

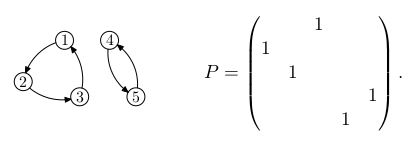
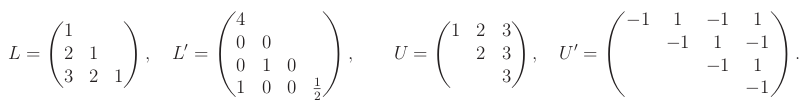

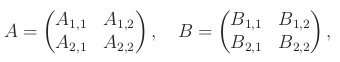
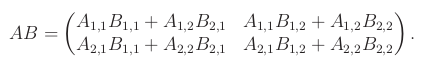


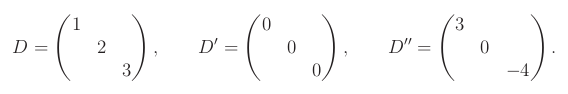
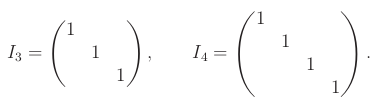

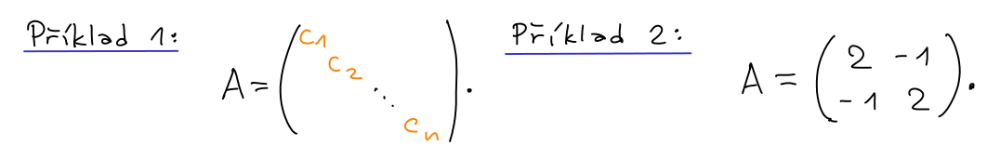
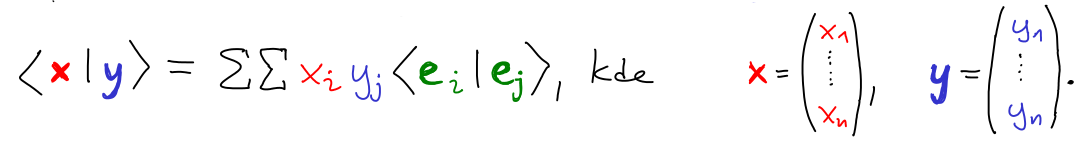
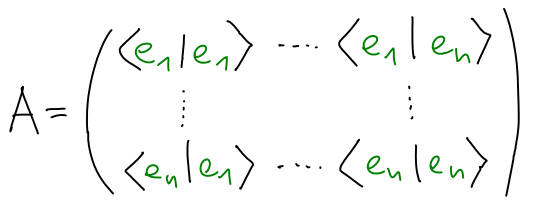 Jako A zvolíme Gramovu matici tvořenou skalárními součiny ⟨ei | ej⟩. Potom je ⟨x | y⟩ = xTAy. Z vlastností 2 a 3 skalárního součinu vyplývá, že A je symetrická pozitivně definitní matice.
Jako A zvolíme Gramovu matici tvořenou skalárními součiny ⟨ei | ej⟩. Potom je ⟨x | y⟩ = xTAy. Z vlastností 2 a 3 skalárního součinu vyplývá, že A je symetrická pozitivně definitní matice.


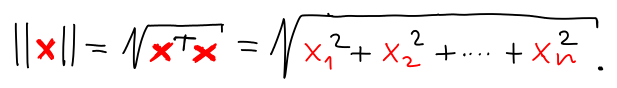



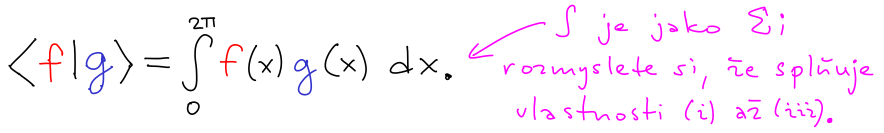
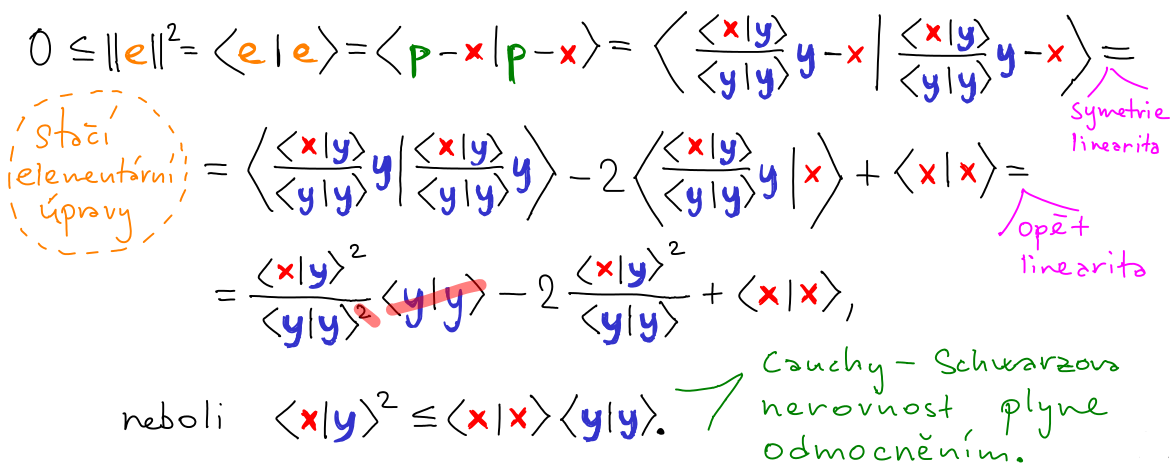

 Tvrzení: Nechť B je uzavřená omezená podmnožina ℝn, symetrická podle počátku. Nechť S je hranice B a 0 ∉ S. Potom je zobrazení ∥⋅∥ : ℝn ⟶ ℝ, kde
Tvrzení: Nechť B je uzavřená omezená podmnožina ℝn, symetrická podle počátku. Nechť S je hranice B a 0 ∉ S. Potom je zobrazení ∥⋅∥ : ℝn ⟶ ℝ, kde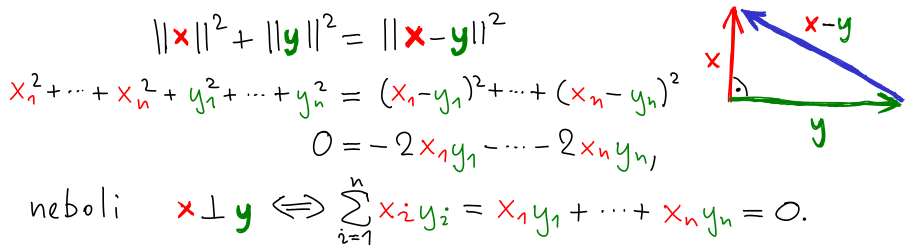


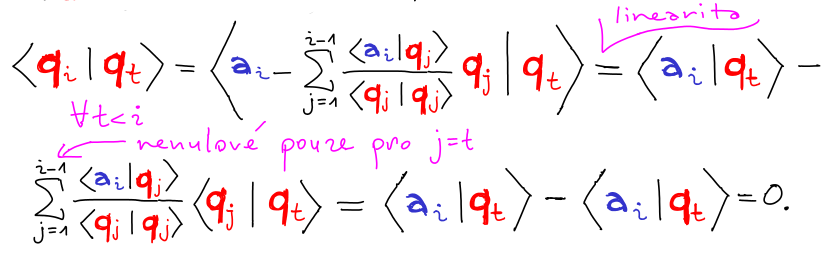
 Mějme dva vektory x a y. Chceme nalézt kolmou projekci x na přímku ⟨y⟩. Ekvivalentně je kolmá projekce vektor přímky, který je nejbližší k x.
Mějme dva vektory x a y. Chceme nalézt kolmou projekci x na přímku ⟨y⟩. Ekvivalentně je kolmá projekce vektor přímky, který je nejbližší k x.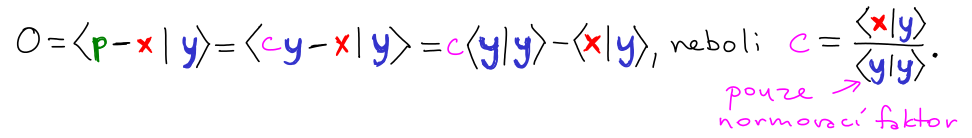
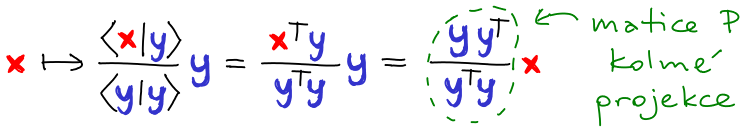
 2. Charakteristika kolmosti projekce: PT = P. Ker(P) je tvořen vektory, které se projektují na 0, což jsou přesně vektory kolmé na Im(P). Tedy Ker(P) = Im(P)⊥ a z fundamentální věty lineární algebry je Ker(P) = Ker(PT) a R(P) = Im(P).
2. Charakteristika kolmosti projekce: PT = P. Ker(P) je tvořen vektory, které se projektují na 0, což jsou přesně vektory kolmé na Im(P). Tedy Ker(P) = Im(P)⊥ a z fundamentální věty lineární algebry je Ker(P) = Ker(PT) a R(P) = Im(P).